城轨沿线地面环境振动响应的半解析有限元求解

崔高航， 欧阳浩然， 陶夏新， M Shamim Rahman

(1.东北林业大学 土木工程学院，哈尔滨 150040；2.哈尔滨工业大学 土木工程学院，哈尔滨 150040；3. North Carolina State University, Department of Civil, Construction and Environmental Engineering, Raleigh, NC 27695)

城轨交通已经成为了城市居民不可替代的交通方式，它带给了我们出行快捷方便的同时，也带来了一些新问题。近年来，城轨交通沿线环境振动的影响越发引人关注。城轨交通引起的振动响应向外传播对周围建筑物产生二次振动和噪声，人们的生活和工作都受到了不同程度上的影响，所以有必要对城轨交通引起的环境振动进行研究。

过去对于环境振动的问题经常使用经验模型进行预测研究，对试验数据过于依赖，应用面较窄。近年来国内外研究人员开始采用解析方法和数值模拟的方法来研究环境振动问题，取得了一些成果。Kang等[1]研究了铁道车辆振动引起的车身的动力学行为。Takemiya[2]则进行了很多列车-轨道模型的简化工作。Sheng等[3]将轨枕模拟为拥有连续质量和刚度的刚体。Ju[4]和Chen[5]分别提出两种预测环境振动的方法，一种是半经验评价方法，另一种是使用有限元模型进行模拟的数值预测方法。王福彤等[6]通过现场观测对城轨交通引发的地表竖向振动进行了分析。朱志辉等[7]建立了高速列车的车-桥耦合系统的随机振动模型。笔者发现已有的研究成果中，研究的方法可以大致分成两种：解析法和有限元法。然而只使用解析法进行求解会由于计算过程中简化条件过多造成与实测数据相差较大的情况。但是只使用有限元法存在建立的模型过于复杂导致对计算机配置的要求很高而且对工程实例不具有通用性。本文在这些基础上对文中的问题采用半解析有限元法进行求解，最后利用北京市某城轨线路区间站之间的环境振动观测数据对计算结果进行验证，验证结果良好。本文的计算方法对于评估现有线路和规划线路附近的环境振动具有一定的实用价值。

1 车辆-轨道-地基土动力相互作用模型

本文建立的解析模型由三个子模型组成分别是车辆模型，轨道模型和地基土模型。

1.1 车辆模型

如图1所示，采用二系悬挂车辆模型[8]。车体和转向架都考虑沉浮和点头两个自由度，轮对仅考虑沉浮一个自由度。

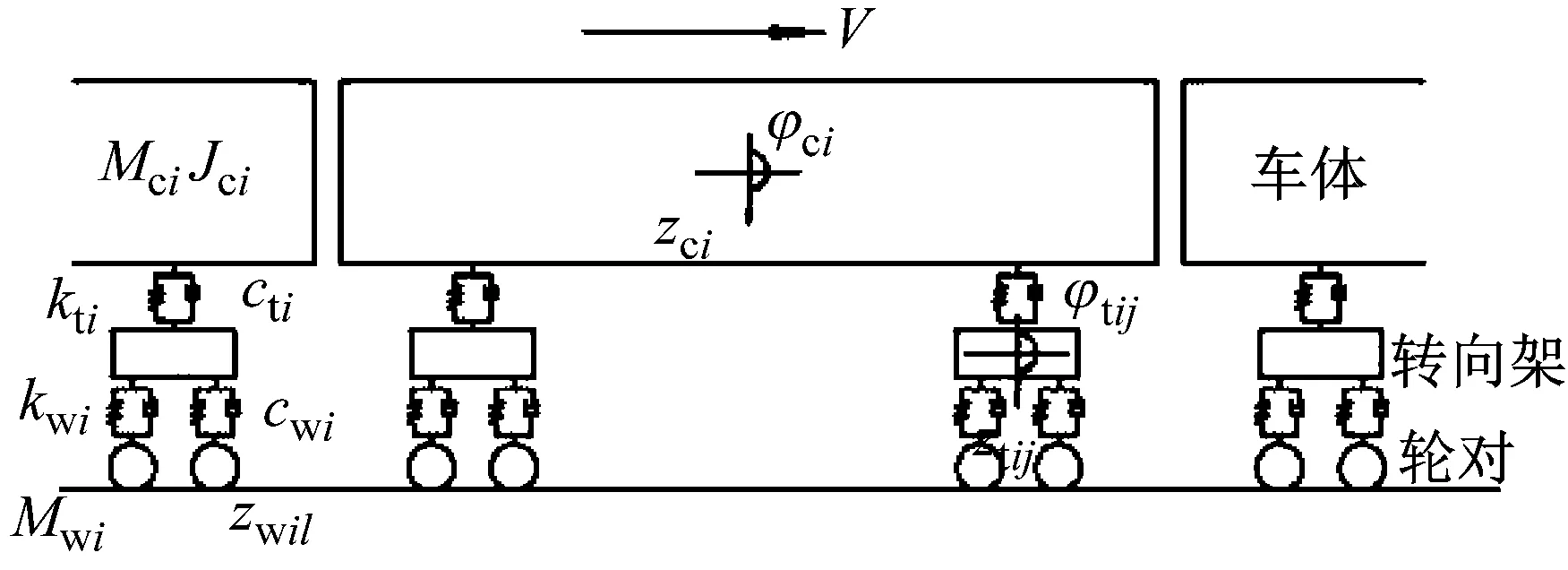
图1 车辆模型计算简图

根据车辆动力学，第i节车辆的平衡方程为：

(1)

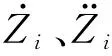
为了进行频域分析，对式(1)进行Fourier变换：

(2)

(3)

在式(2)的基础上，车辆的振动位移可以表示成：

(4)

(5)

式中：系数矩阵B=DT=[06×4|I4×4]。

将式(5)代入式(4)中得到第i节车辆的轮对位移向量为：

(6)

将式(6)进一步简化可写为：

(7)

不同车辆的振动是相互独立的，式(7)能够被应用于N节车辆的轮对位移，可以用一个向量方程组表示：

(8)

1.2 列车-轨道相互作用模型

根据资料调研和城轨列车实际运行速度，轮轨间的振动变形近似于弹性变形，本文采用Hertz弹性接触理论。根据上述假设的条件，存在如下关系式：

(9)

式(9)在频域内可表示为：

(10)

容易知道所有轮轨接触点应满足等式(10)，因此可以用一个向量方程组表示：

(11)

1.3 轨道支撑结构相互作用模型

图2为轨道支撑结构模型。在建立此模型期间进行了以下假设：

(1) 钢轨被认为是无限长的欧拉伯努利梁，且截面尺寸保持不变；

(2) 钢轨与轨枕、轨枕与道砟、道砟与地基土之间的连接用弹簧-阻尼器模拟；

(3) 认为轨枕和道砟是离散支承的质量块；

(4) 因为地基的位移很小，不影响振源传递给地基的力，所以假定地基的位移为0。

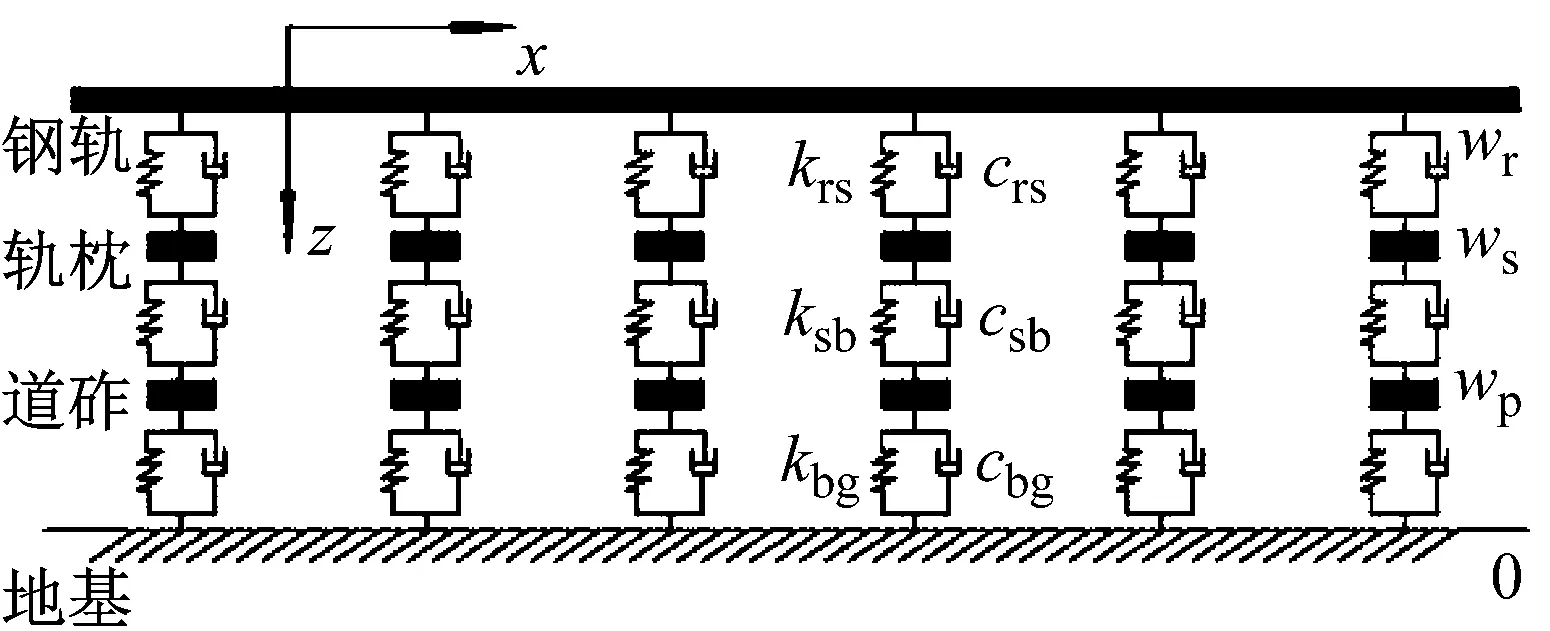
图2 轨道支撑结构模型

如图3所示，钢轨由轨枕离散支撑，钢轨受到的单个轮对的荷载等于2n+1个轨枕的支撑荷载。当单个轮对荷载P(t)以速度V移动时，轨道振动的偏微分方程根据假定可以得到：

(12)

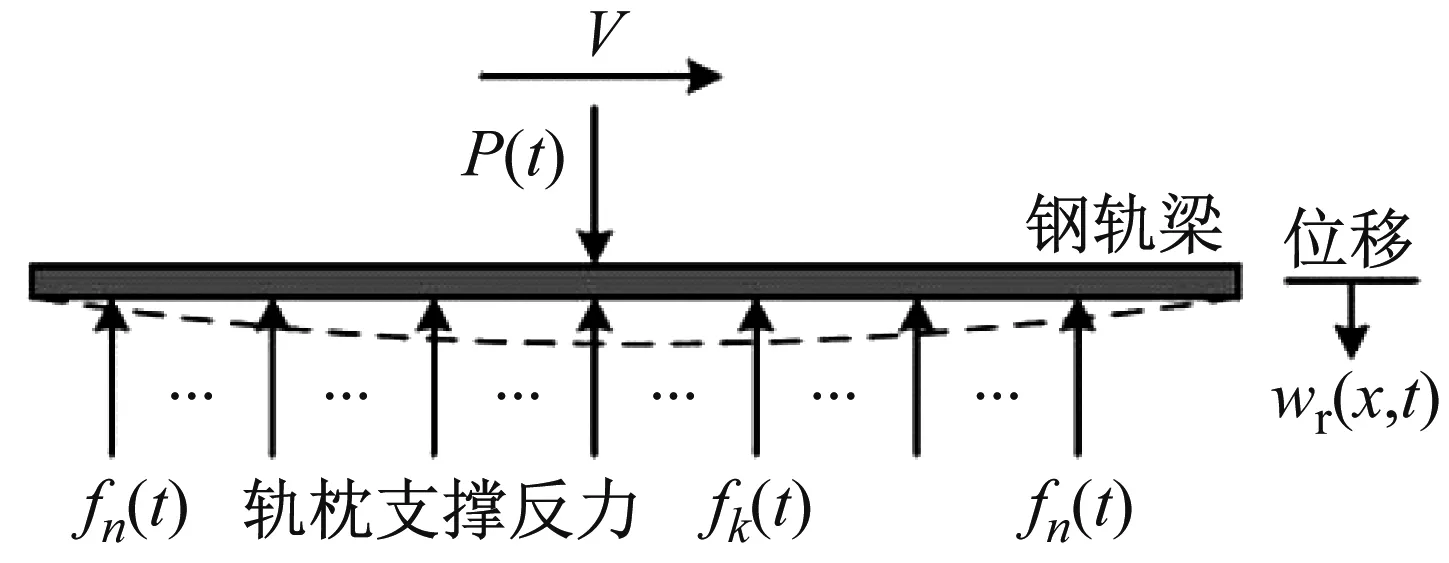
图3 受力简图

经推导[9-10]，钢轨的竖向总位移为：

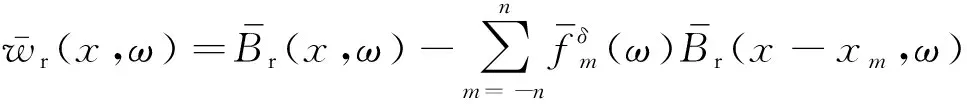
(13)

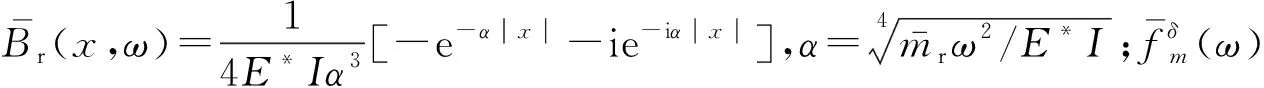
先后取单个轨枕，单个道砟作为受力分析模型，并根据受力平衡得到轨枕和道砟的平衡方程结合弹簧阻尼器参数，最终可以得到地基反力。

1.4 振源模型输出力的求解

为了得到地基反力，需要先计算轮轨相互作用力。由式(11)可知，等式左边的矩阵由轮轨相互作用力向量组成；等式的右边分别是列车所有轮对的位移向量、钢轨位移向量和轨道不平顺位移向量。轮对位移和轮轨相互作用力之间的关系由公式(8)给出，同时采用实测数据为轨道不平顺的输入。因此要求出轮轨相互作用力，就只要获得钢轨位移向量与轮轨相互作用力向量之间的关系，代入等式(11)即可求得。

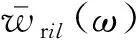
(14)

式中：ωk为单一波长轨道不平顺对应的激振圆频率；i′和l′分别表示车辆的节数和每节车辆的轮对编号；xpil-xpi′l′表示列车轮对之间的距离。

式(14)对每个轮轨接触点都是满足的，因此以矢量方程组的形式表示为：

(15)

(16)

将式(8)、(15)代入到式(11)获得频域内所有轮对的轮轨相互作用力向量：

(17)

其中Q矩阵表示如下：

2 算例分析

根据上节所建立的模型编制了Fortran计算程序，再利用有限元软件ABAQUS建立了地面振动传播路径模型。本节将通过环境振动观测数据分析与对比模型的计算结果。

2.1 计算参数的选取

选取的列车编组为4节编组，单节长度为19 m，车速为72 km/h，车辆模型的基本参数如表1所示。轨道系统中每个部件的参数如下：

表1 车辆模型基本参数

钢轨：单位长度质量为mr=60.64 kg;截面刚度EI=6.62×106N·m2;结构阻尼比ξr=0.01。

轨枕：质量ms=252 kg;间距d=0.605 m。

道砟：质量mb=1 360 kg。

钢轨和轨枕之间的弹簧-阻尼系数：krs=4.0×107N/m，crs=1.24×105N·s/m。

轨枕和道砟之间的弹簧-阻尼系数：ksb=7.8×107N/m，csb=6.5×104N·s/m。

道砟和地基土表面之间的弹簧-阻尼系数：kbg=2.4×108N/m，cbg=5.88×104N·s/m。

轨道不平顺：如图4所示，输入中国某铁道竖向轨道不平顺观测记录[11]。

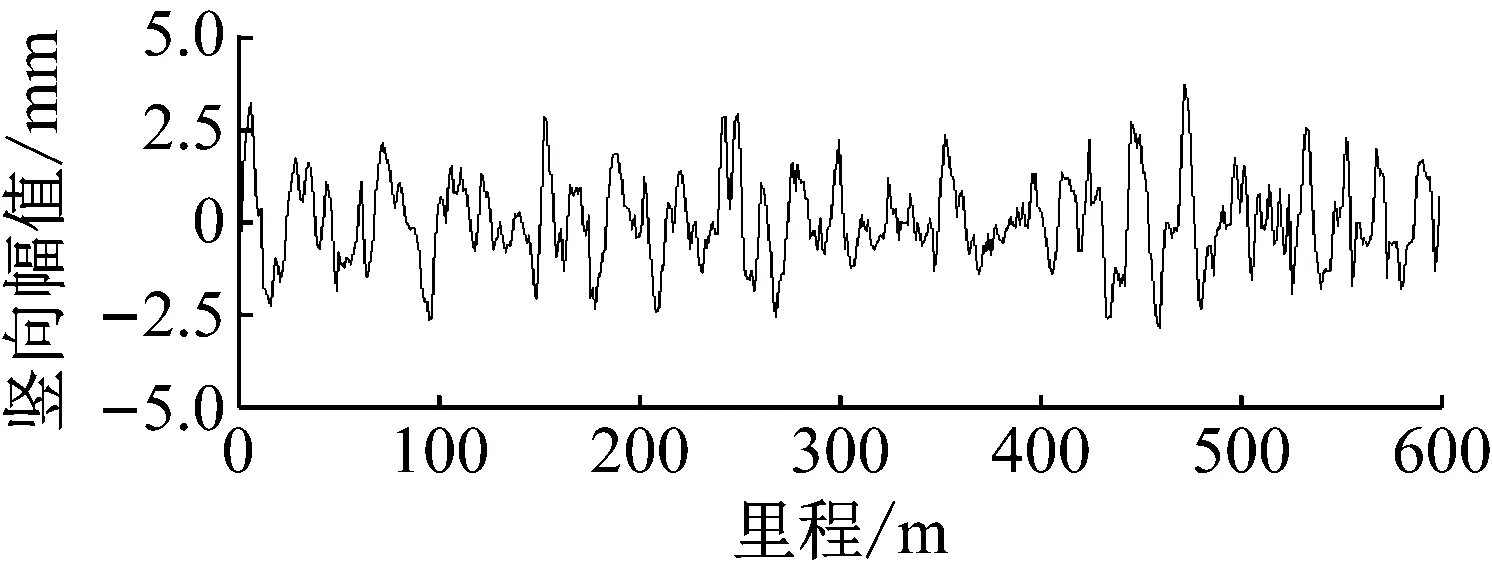
图4 轨道不平顺时程图

2.2 传播路径模型

在建模的过程中，由于道床块的上部承受着由轨枕传递的轮轨力，对于钢轨而言轨枕是离散的支撑，所以道床块对地基的力可以简化为离散分布的点振源阵列。同时在建模过程中考虑问题的简化和对称性，取沿线轨道一侧的一半的地基土进行分析。

场地为北京某地铁两站之间的一个区段，勘察获得的钻孔资料列于表2。场地模型沿列车运行方向取长150 m，垂直轨道方向的宽度取70 m，竖向深度取40 m，网格划分如图5显示，每个单元均为0.5 m×0.5 m×0.5 m。边界条件采用无限元边界[12-13]，该边界能够将振动波衰减到无限远处，避免了波动在有限元边界处的损耗，同时线路中心线所处的YZ平面的边界采用对称边界条件。

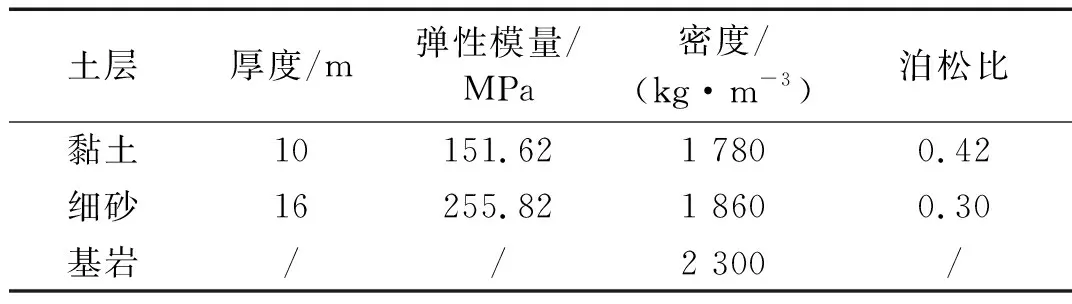
表2 场地钻孔资料

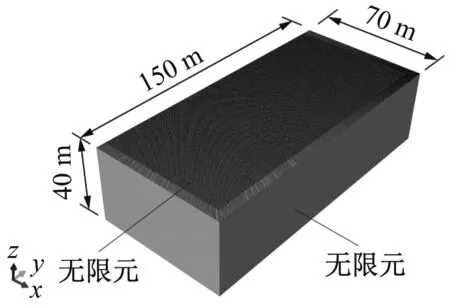
(a) 模型总图

(b) 模型局部放大图

2.3 计算结果分析

施加的荷载时程由编制的Fortran计算程序所求得，如图6所示。在距轨道轴线10 m、20 m、40 m、50 m、60 m处，计算这5个点的竖向加速度时程，如图7所示。并于表3中比较了模型计算与实测数据的地表加速度峰值的偏差。

从表3结果可知：

(1) 对于地面的振动，地面的竖向加速度随着传播距离的增加而减小。同时在距轨道中心线50 m处的竖向加速度计算值峰值为0.001 98 m/s2，而在距轨道轴线60 m处为0.002 81 m/s2，涨幅有29.53%，对于实测值涨幅则有22.62%，说明在距离轨道中心线较远的地方出现了加速度反弹增大的现象。

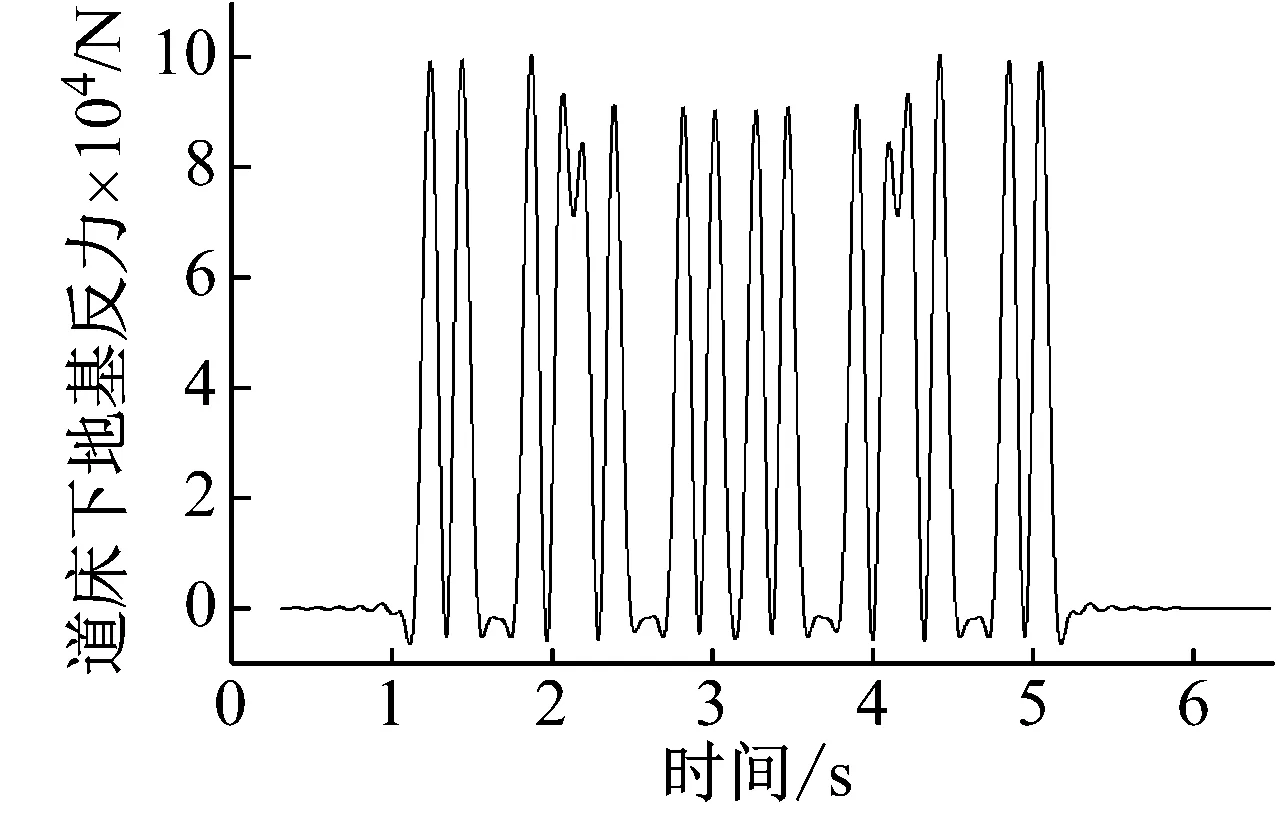
图6 输入荷载时程图

(2) 计算得到的加速度时程与观测记录峰值大小接近，响应的持时相当。为了更具体地比较加速度的峰值，表3列出了计算值与实测值的峰值，并定义计算值与实测值之差除以实测值的绝对值为偏差率，可以得到偏差率的范围为6.50%～16.10%，平均值为9.44%。以上结果表明，本文的计算方法是可信的。

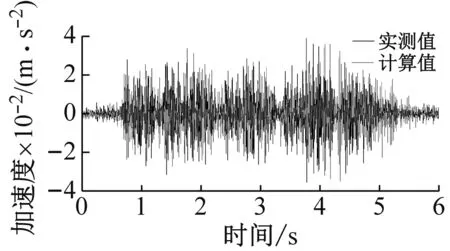
(a) 10 m处的地表竖向加速度时程

(b) 20 m处的地表竖向加速度时程

(c) 40 m处的地表竖向加速度时程

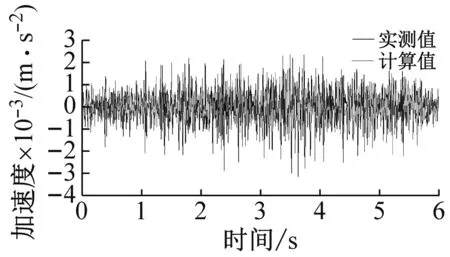
(d) 50 m处的地表竖向加速度时程

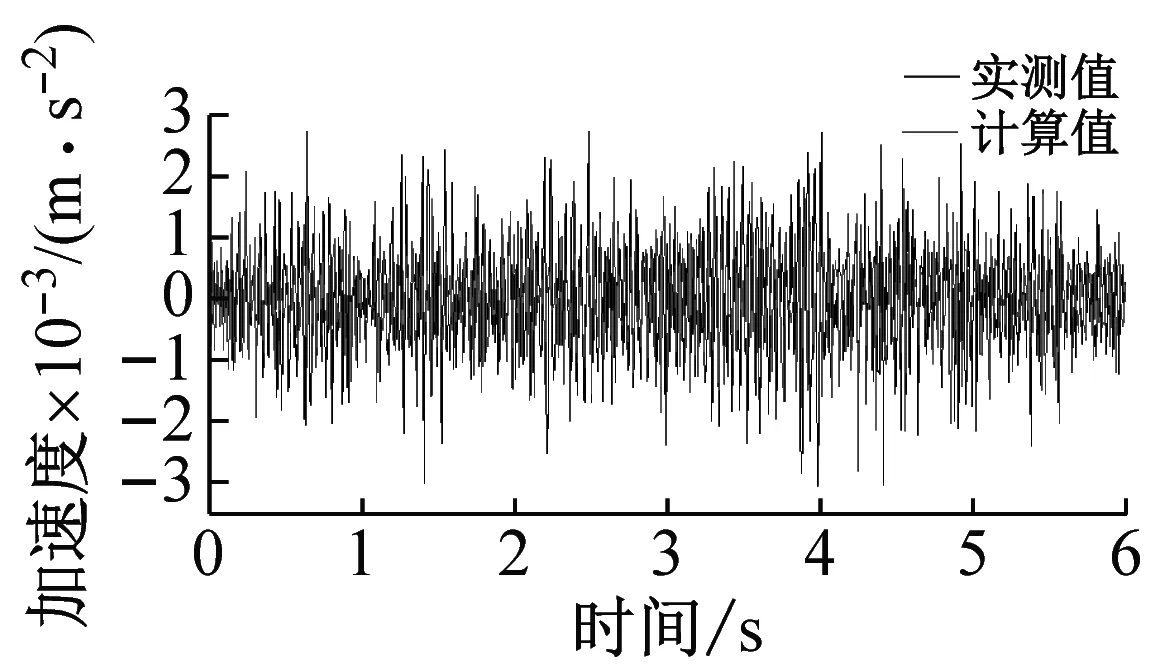
(e) 60 m处的地表竖向加速度时程

图7 地面5处加速度响应的实测值与计算值的比较

Fig.7 The comparison of results with the observations at five ground points

表3 地表加速度计算值峰值与观测值峰值的比较

Tab.3 Peak ground accelerations of the results with those recorded

响应类别计算值观测值偏差率/%10 m加速度/(m·s-2)0.035 610.038 547.6020 m加速度/(m·s-2)0.019 520.021 489.1240 m加速度/(m·s-2)0.005 750.006 156.5050 m加速度/(m·s-2)0.001 980.002 3616.1060 m加速度/(m·s-2)-0.002 81-0.003 057.87

图8显示了列车运行速度为72 km/h时对距轨道轴线10 m、20 m、40 m、50 m、60 m处的5个加速度频谱曲线。由图7可以看出，波在土中的传播受到土中的材料阻尼和辐射阻尼的影响，随着距离的增加，加速度频谱中的高频成份变得越来越少。同时经过快速傅里叶变换后，实测值与计算值的频谱相比，二者的优势频率十分接近，也再一次证明了模型的有效性。

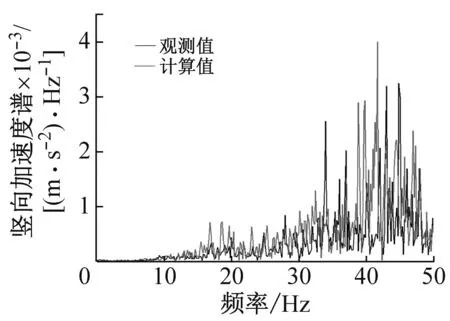
(a) 距轨道10 m处的结果比较

(b) 距轨道20 m处的结果比较

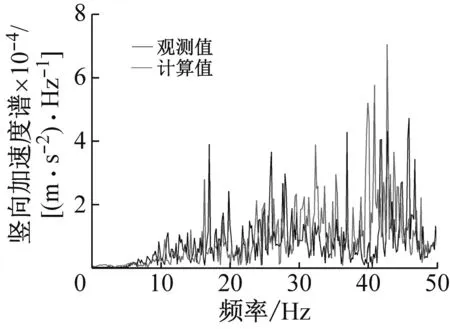
(c) 距轨道40 m处的结果比较

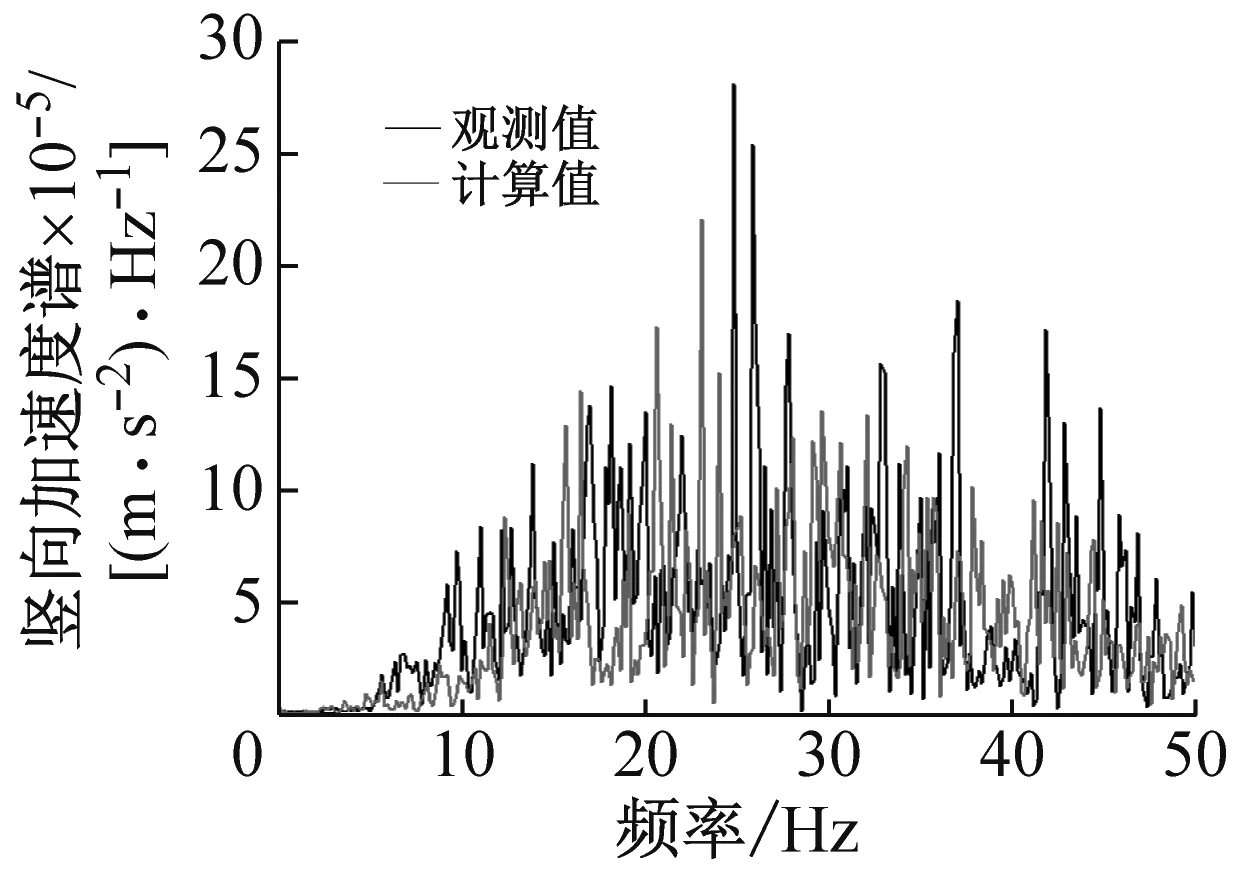
(d) 距轨道50 m处的结果比较

(e) 距轨道60 m处的结果比较

图8 地表5点加速度频谱与观测结果的比较

Fig.8 Comparison of acceleration spectrum of five ground points with observation results

3 结 论

本文提出了一种基于半解析有限元模型的城轨列车运行时引起的环境振动的计算方法。方法有两个步骤：地基反力的求解和地面振动的求解。最后算例的结果表明：

(1) 地面环境振动响应随传播距离的增加而减小，在传播到一定距离时出现了加速度反弹增大现象。

(2) 随着传播距离的增大，加速度频谱中的高频所占比重越来越小。

(3) 本文发展的这套计算车辆-轨道-地基土系统振动反应的方法是有效的。