铁路集装箱旅客化运输系统开行方案分阶段编制方法研究

夏 阳， 魏玉光， 赖艺欢， 张 琦

(1. 北京交通大学 交通运输学院， 北京 100044； 2. 深圳市城市交通规划设计研究中心， 广东 深圳 518034；3. 深圳市交通信息与交通工程重点研究室， 广东 深圳 518034)

近来年，随着我国经济结构的调整，铁路货物运输市场发生了较大变化，白货运输的需求大幅度增长，同时货主对运输时效性的要求也逐渐提高。在此背景下，铁路集装箱运输将在货物运输中扮演更重要的角色，但目前我国铁路集装箱运输的市场占有率远远低于公路运输。因此，优化铁路集装箱运输组织，提高铁路集装箱运输竞争力具有重要的现实意义。

通过运输流程再造，文献[1]构建了铁路集装箱旅客化运输快捷系统(新型集装箱系统)。在新型集装箱系统中，集装箱列车采用固定车底编组的形式，在运行过程中无需解体，且在始发终到站和沿途经停站使用到发线装卸作业模式，运输组织脱离编组站，实现了列车的旅客化开行。此外，新型集装箱系统基于既有路网构建了集装箱运输三级节点系统，以发挥网络运输的优势。此套系统能够大幅提高铁路集装箱的送达速度，缩短运到期限，使铁路集装箱运输具备与公路运输竞争的条件。

为保证新型集装箱系统的运营效果，本文将研究其列车开行方案问题。目前，仅有文献[2-4]对新型集装箱系统列车开行方案进行了研究。其中，文献[2]根据基于OD的箱流需求数据，优先确定列车径路，进而求解列车频率和停站方案，此方法能解决单条线路或小规模路网的开行方案编制问题，无法适用于大规模路网。文献[3]构建了针对大规模路网场景下的列车开行方案优化模型，并设计了模拟退火算法进行求解。文献[4]基于文献[3]的研究，进一步考虑了新型集装箱系统的运输组织模式，并基于此对列车开行方案进行研究。但文献[3-4]均未考虑线路及车站能力的约束。针对旅客列车开行方案问题，文献[5]预先设定了旅客出行可行路径集，在此基础上建立优化开行线路及列车频率，并采用列生成求解算法，但该模型未考虑旅客换乘的情况。文献[6]设计了“Change & Go”换乘网络，并从旅客个体最优的角度出发构建了旅客列车开行方案的优化模型。文献[7]在构建列车服务网络时考虑了列车停站方案，并基于网络流理论构建了列车开行方案优化模型，设计拉格朗日松弛算法进行求解。文献[8-10]以荷兰铁路系统(IC快车、IR中速车和AR慢车)为研究对象，分别以运输企业和旅客为导向建立了列车开行方案模型。文献[11]均衡考虑企业利益和旅客需求，建立了旅客列车开行方案双层规化模型，并设计模拟退火算法求解。文献[12]则以台湾高速铁路线为研究对象，同时考虑列车频率、停站方案以及所需车底数量，构建了列车开行方案模型。针对货物列车开行方案问题，目前一般采取分阶段编制的方法，即优先确定车流径路，在此基础上研究货物列车编组方案。文献[13]研究了车流径路优化问题，并设计了拉格朗日松弛算法进行求解。文献[14-15]针对编组方案问题构建了优化模型，且均采用启发式算法进行求解。

基于文献[3]提出的运输组织模式，本文考虑车站及线路能力的约束，借鉴货物列车开行方案的编制思路，提出新型集装箱系统列车开行方案的分阶段编制方法。该方法采用基于“备选集”的优化思想，综合考虑了企业利益和货主利益，同时继承了货运系统中货物运输方案(物理径路和编组方案)唯一性的特点。

1 开行方案分阶段编制方法

新型集装箱系统列车开行方案分阶段编制方法共包含3个阶段，分别为箱流径路优化、箱流归并和快速集装箱列车开行方案编制。首先，确定各支箱流的运输物理径路；其次，将办理站产生的箱流归并至路径前方专办站或中心站，从而转化为可通过快速集装箱列车[3]运输的箱流；最终，编制快速集装箱列车开行方案，从而完成新型集装箱系统开行方案的整体编制。

1.1 箱流径路优化

与旅客不同，集装箱不具备自主能动性，因此，在编制开行方案时，可预先确定各OD间箱流的运输物理径路。为了降低运输组织工作难度，规定同一OD间箱流的物理径路具有唯一性，与传统货运系统中同股车流不可拆分的性质类似。此外，在实际运输过程中由于车站和区段通过能力的约束，各支箱流不能完全依最短路径运行，需要优化箱流径路。

为方便建模，做出以下假设：

(1) 各OD间的箱流量已知。

(2) 各路段通过能力已知。

(3) 由于路网中车站能力可转化为区段能力，故在建模时不考虑车站能力对箱流分配的制约。

定义路网为一个有向图G=(S,A)，S为路网中三级集装箱节点集合且∀i,j∈S，A为路网中有向弧(i,j)集合，其中每一条弧含有里程、最大通过速度和通过能力3个属性。路网上箱流OD集合为W={w=(wo,wd)|wo,wd∈S}，其中wo、wd分别表示需求的产生地和目的地。构建箱流径路优化模型M1为

( 1 )

( 2 )

( 3 )

模型M1中，式( 1 )为目标函数，表示最小化总的箱流在途时间；式( 2 )为流量守恒约束，同时也表明路网中箱流物理径路的选择具有唯一性；式( 3 )为路段通过能力约束。

模型M1为整数规划模型，可利用商业求解软件求解。值得说明的是，箱流径路优化问题预先实现了箱流在路网中的分配，可类比传统货运系统中的车流径路优化问题，且二者在数学模型形式上相同。此外，当考虑不可行流时，文献[13]给出了具体的改进模型，同时给出了使用拉格朗日松弛算法求解的具体过程。

1.2 箱流归并

根据运输组织模式，在获得箱流物理径路后，部分办理站与其他站点间的箱流运输方案也随之确定，而剩余办理站产生的箱流可进行归并处理，转化为可通过快速集装箱列车运输的箱流。具体处理过程如下：

(1) 办理站与同区段站点间的箱流办理站a与同区段内的其他车站A、b和B间的箱流通过区段集装箱列车1进行输送，见图1。办理站b同理。

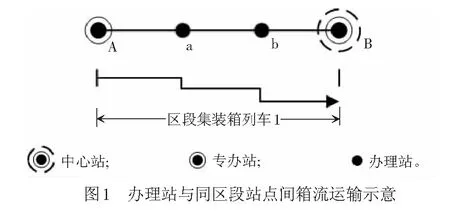
(2) 办理站与相邻区段办理站间的箱流办理站a(b)与c、C间的箱流需要通过区段集装箱列车1和区段集装箱列车2进行运输，见图2。

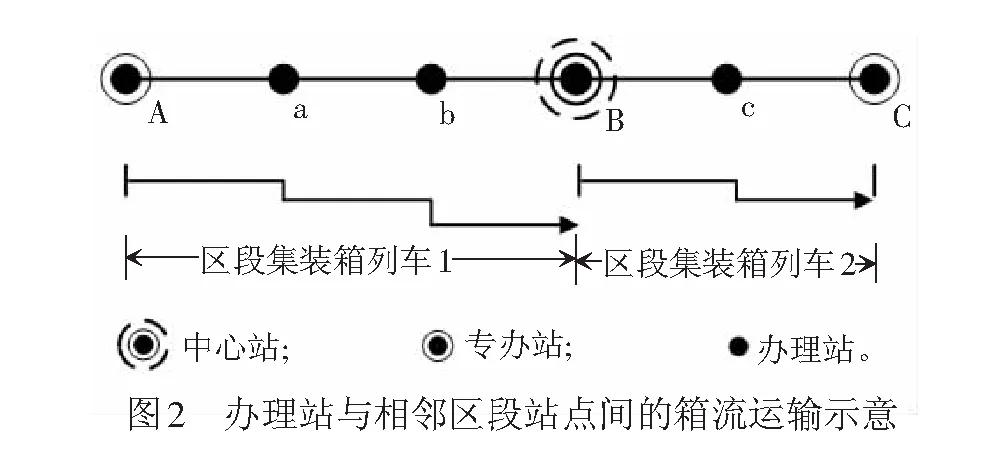
(3) 办理站与跨区段站点间的箱流假设求得a和e间的箱流径路为a-B-C-D-e，则可将a和e间箱流归并至BD间箱流，见图3。在第三阶段快速集装箱列车开行方案确定后，可获得BD间箱流的运输方案，进而得到ae间运输方案。同理，C和e间箱流可归并至CD间箱流。

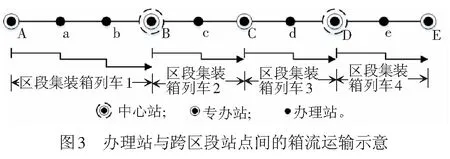
1.3 快速集装箱列车开行方案

在箱流归并阶段后，需确定中心站和专办站所产生箱流运输方案。考虑到快速集装箱列车与旅客列车的相似性，可通过编制快速集装箱列车开行方案解决此问题。

参考旅客列车开行方案定义，快速集装箱列车开行方案可定义为：针对中心站和专办站产生的集装箱，以系统运输特点和箱流量为依据，确定快速集装箱列车运行起讫点、物理路线、停站方案、运行频率以及编组情况，并尽可能让特定目标(集装箱运输总时间或企业成本等)最优化。

本文采用编制旅客列车开行方案的“备选集”法进行建模。此外，将铁路网中将连接办理站的路段进行归并，形成只具有中心站和专办站的铁路网。

建模前，做出以下假设：

(1) 由于在箱流径路优化阶段已经考虑了区段通过能力的约束，此阶段不再考虑能力约束。

(2) 列车编组相同(车底采用平板车)，即列车能力相同。

(3) 如运输组织模式分析部分所述，列车在沿途中间站均停车，即列车为站站停列车。

定义归并后的路网为一个无向图G′=(V,E)，V为路网上中心站和专办站集合，用i,j,k进行索引，E为路网中的线路区段集合且∀e∈E，则运行线路可用l=(i,k,…,j)表示。设V0⊆V为可以作为线路始发或终到站的车站集合，连接起始站和终到站之间的物理径路可由最短路法或k短路法确定，备选集中的线路代表可能的列车运行经路，则备选集L={l|l=(i,k,…,j),i,j∈V0}。

基于此，可构建快速集装箱列车开行方案优化模型M2为

( 4 )

( 5 )

( 6 )

( 7 )

( 8 )

模型M2中，式( 4 )、式( 5 )为目标函数。其中式( 4 )为最小化企业成本，由开行列车的固定成本和可变成本两部分构成；式( 5 )为最小化总的箱流换乘次数。集装箱运输时间由4部分构成，分别为发车前作业时间、在途时间、列车停站时间和换乘时间。其中在途时间和停站时间在获得物理径路后也随之确定，发车前作业时间可取平均值。因此本阶段仅最小化总的箱流换乘时间。由于具体的换乘方案和列车时刻表未知，换乘时间难以确定，可通过惩罚法进行处理，即规定每发生一次换乘，则增加一个固定的时间惩罚值。但在式( 5 )中，此惩罚值被视为参数去除，从而将目标含义转化为最小化总的箱流换乘次数。此外，某支箱流在运输物理径路上的换乘次数等于运输过程中使用线路的数量减1。例如，箱流w需要利用线路l1、l2和l3完成运输，则运输过程中发生2次换乘作业；式( 6 )保证了运输箱流使用的线路必须覆盖其物理径路上的每一个区段；式( 7 )为只有当线路l开通时，箱流才能使用该线路；式( 8 )为以线路上输送箱流量最大的区段来计算列车开行频率，其中每辆平板车可装载2个集装箱。

模型M2为多目标整数规划模型，可采用线性加权和法将模型转化为单目标模型，同时去除式( 5 )中的常数项，则转化后的目标函数为

( 9 )

式中：α、β为目标函数权重系数，α,β>0，α+β=1。

转换后模型同样可利用商业求解软件进行求解。

2 开行方案编制特点分析

一方面，在新型集装箱系统列车开行方案分阶段编制方法中，箱流物理径路优先被确定。这与传统货运系统中车流径路问题相同，且沿袭了同股车流(箱流)不可拆分的特点。

但同时必须明确，在传统货物运输中，由于运量分散，大量白货需多次经编组站改编中转输送，其运输计划通过编制技术站列车编组计划确定。编组计划本质上为货物列车接续服务问题(freight train connecting service problem)。而在新型集装箱系统中，白货的运输计划通过编制快速集装箱列车开行方案解决。快速集装箱列车组织过程与旅客列车相同，运行中无需解体，避免了货物进入编组站进行改编作业。因此，快速集装箱列车开行方案优化模型M2与编组方案优化模型(见文献[10])在本质上不同。

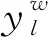
为方便理解，考虑一条由3个车站构成的简单线路网络。假设不论是旅客列车开行方案还是快速集装箱列车开行方案，优化结果是开通l1和l2两条线路(列车径路)，见图4。在旅客列车开行方案优化结果中，ab间客流一部分利用线路l1完成运输，另一部分用线路l2完成运输，bc和ac间客流则被分配至线路l1上；在快速集装箱列车开行方案优化结果中，ab间箱流只能通过线路l2进行运输，线路l1则承担bc和ac间箱流的运输任务。

3 案例分析

3.1 参数及计算结果

鉴于箱流径路优化与车流径路优化本质上相同，且通过能力对箱流在路网中分配的影响并非本文的研究重点，因此，本文仅对第三阶段快速集装箱列车开行方案进行案例分析，同时假设箱流径路优化阶段的结果(各支箱流的运输物理径路)已知。

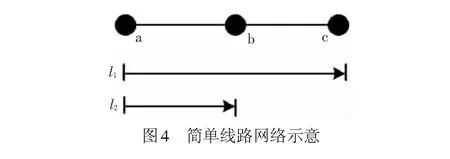
本文选取18个集装箱中心站作为一级节点，同时加入部分口岸站、港口和其他内陆站点作为二级节点，以此构建快速集装箱列车运输网络，见图5。

模型求解所需其他参数取值见表1。

表1 参数取值

在本案例中，设18个集装箱中心站以及连云港站、厦门站、阿拉山口、二连浩特站和满洲里站可作为线路的始发终点站，其相互之间的最短路构成了备选线路集，在删除部分不合理线路后，备选线路集含有169条线路。

使用Python 3.6调用CPLEX 12.6求解器进行混合编程测试案例。设置目标函数权重系数均为0.5，设置CPLEX的Gap参数为0.01，在4 G内存、Intel 2.53 GHz的计算环境下，通过19 min的计算获取结果。计算结果表明需开通33条线路，固定成本为6 600 万元，可变成本为12 111 万元，共有702对OD在运输过程中需进行换乘作业。具体开通线路和各线路运行列车频率见表2。

表2 开通线路及列车运行频率

通过求解模型，路网中各OD间箱流的运输方案也被确定下来。在此，仅列出6对OD对间箱流的运输方案，见表3。

表3 部分OD间箱流的运输方案

以衡水—沈阳间的集装箱为例，说明运输方案的唯一性。衡水—沈阳间箱流的运输物理径路为衡水—北京—秦皇岛—沈阳，箱流需在北京中心站换乘一次。事实上，多条线路经过衡水—北京区段，如京九线，但模型求得结果此区段将只能使用北京—厦门的线路进行运输。同理，北京—沈阳区段将使用二连浩特—哈尔滨线路运输。

3.2 灵敏度分析

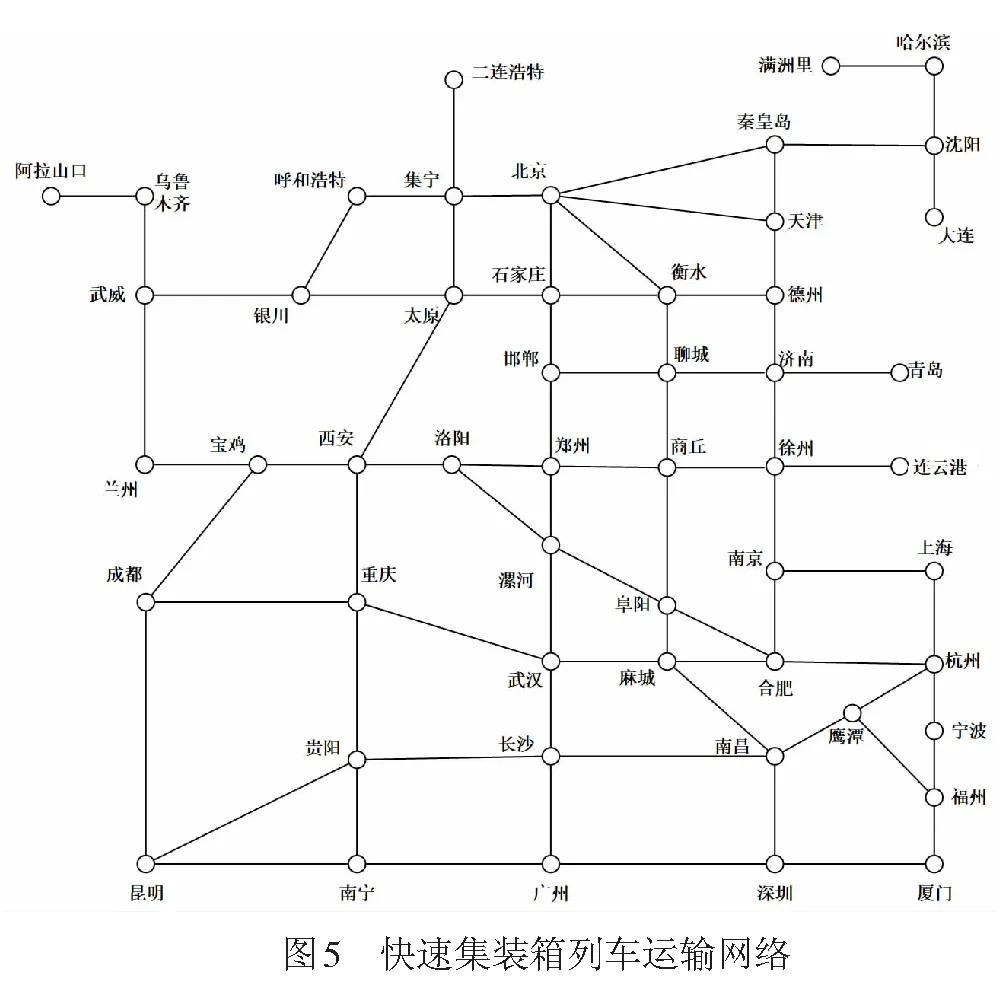
对不同的α和β取值进行灵敏度分析，测试权重系数对目标函数的影响。设置α和β的取值间隔为0.1，从而产生11个组合。用0.001代替取值为0的情形，避免得到无意义结果。不同取值计算结果见表4。

表4 α和β不同取值计算结果

随着成本权重系数的增大，开通运行线路的数量逐渐减少，成本也随之下降。但与此同时，路网中需换乘的OD数量变多，总箱流换乘次数不断增大。结果体现了企业利益与货主利益间的博弈关系。一方面，开通较少数量的线路来满足箱流需求可以减少运营成本；另一方面，箱流分配的结果会使得更多的集装箱需要通过若干次中转换乘才能被输送到终到站，从而增加集装箱旅行时间，降低服务质量。

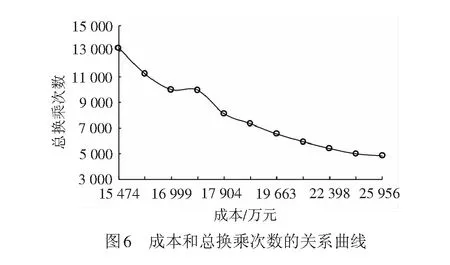
最后，选取总成本和总换乘次数两项数据构建近似帕累托前沿，以表示两者间的博弈关系，见图6。从图6中可以看出，当α从0.7变为0.8时，两点间连线近似为水平线，表明此时成本减少但总换乘次数只小幅增加；当α从0.6变为0.7时，两点间连线斜率最大，意味着此时减少相同成本，总换乘次数增长幅度最大；而对于其他点间的连线，可以看出总换乘次数与成本间保持近似线性关系。

4 结束语

本文提出的新型集装箱系统列车开行方案编制方法综合考虑了货主与铁路企业的利益，且在箱流径路优化阶段优先加入能力约束，确定箱流运输物理径路，从而减小快速集装箱列车开行方案的编制难度。通过案例分析，验证了提出方法的可行性，同时表明了企业利益与货主利益间的博弈关系。论文研究成果对于提高新型集装箱系统运输组织效率具有一定的理论意义。

未来研究中，快速集装箱列车时刻表问题以及开行方案与时刻表协同优化问题将成为研究重点。