动车组高级修计划优化模型及算法研究

武建平， 何君礼, 林柏梁， 王 辉， 张旭辉， 王忠凯

(1. 北京交通大学 交通运输学院，北京 100044； 2. 中国铁路设计集团有限公司 交通运输规划研究院， 天津 300142；3. 中国铁路沈阳局集团有限公司 客运部，辽宁 沈阳 110000; 4. 中国铁道科学研究院集团有限公司 电子计算技术研究所，北京 100081； 5. 中国铁路上海局集团有限公司 车辆部，上海 200071)

高级修计划是动车组运用与检修管理工作的重要组成部分，涵盖三、四、五级检修。由于复杂的检修规程、全年不均衡的客流分布、检修车间有限的检修能力以及长达2～8周的检修耗时(修时)等原因，动车组高级修计划需要以自然年或更长的时间为规划期提前进行编制。编制该计划的主要目的是在合理利用有限检修资源以及遵守既定检修规程的条件下，为计划期内客流长高峰期时期(如春运、暑运等)提供足够的技术状态良好的动车组。该计划是动车组运用计划、动车组二级修计划以及检修基地工作组织的先决条件。

自2008年京津城际铁路开通以来，我国高速铁路取得迅猛发展。按照文献[1]的要求，先期投入运营的动车组在未来几年内会集中进入高级修作业环节。由于高级修修时较长，当该作业发生在客流高峰时期，会因为上线动车组数量不足造成旅客的出行需求无法得到满足，由此带来的不仅是运营收入的损失，还有出行者对铁路运输的满意度下降，而提前检修又会造成检修成本的增加。同时，在检修能力给定条件下，集中送修还会造成修时延长，影响车辆的运用效率。因此，科学地制定出既满足用车需求又尽可能降低检修成本的高级修送修计划是目前高速铁路运输领域亟待解决的一个科学技术难题。

国内外不少专家学者针对相关问题进行了研究，并取得一定成果。Marti等[2-3]以荷兰铁路车辆的预防性检修制度为背景，从整数规划的角度出发，构建了铁路车辆检修计划编制模型。Abbink等[4]以高峰时期能力短缺最小化为目标构建了动车组的运用优化模型，并采用CPLEX进行求解。Alfieri等[5]和 Giacco等[6]针对动车组的定期预防维修问题建立多商品流模型，提前调整运用计划使未来1～3 d内需要检修的动车组及时得到维修。王莹等[7]以动车组可行运用计划为决策变量，以待检动车组检修前的累计运行里程最大化为优化目标，建立动车组检修计划优化模型，并将列生成算法嵌入分枝定界算法进行求解。Li等[8]针对动车组的运用与二级检修计划建立了0-1整数规划模型，考虑了动车组和运行径路之间的匹配关系、动车组的检修要求和动车所的检修能力限制等约束条件。王忠凯[9]构建了动车组运用与检修一体化编制的数学优化模型，针对动车组运用检修计划优化方法，提出带有状态约束的旅行商问题和带拓扑约束的车间调度问题，给出了这两类问题的数学描述，并设计了求解问题的构造图和基于最大最小蚁群优化算法的通用求解方法。以上文献均是针对动车组的运用检修计划编制问题，而专门针对动车组高级修计划问题的研究较少。李燕等[10]提出了一种预测动车组高级修检修量的方法，为高级修计划的编制提供了决策依据。Lin等[11]针对动车组高级修问题，通过设立状态函数构建了0-1整数非线性规划模型，并利用模拟退火算法进行求解。Wu等[12]通过构建时间-状态网络将动车组高级修送修问题转化为网络上的径路选择问题，并构建了相应的数学规划模型与求解策略。在动车组高级修其他相关方面，陈彦[13]、王忠凯等[14]、贾志凯[15]等针对动车组高级修车间工艺流程进行了优化研究。王东屏等[16]、王红等[17]等从单一部件和多部件的维修策略进行了深化研究。到目前为止，针对动车组高级修计划的优化研究仅见于文献[11-12]。

目前，在动车组高级修计划编制的实际工作中仍是借助Excel表，以人工经验编制计划。该方法不仅效率较低，而且易造成动车组过度检修，增加检修成本。在动车组高级修检修量逐年上升的形势下，该方法显然已经不能满足实际的工作需求。在充分借鉴上述研究成果的基础上，本文结合我国动车组高级修计划编制过程中涉及的诸多因素，构建了0-1整数规划模型，并设计了相应的粒子群求解策略，以实现动车组高级修计划的优化。

1 问题描述

动车组的日常检修计划与运用计划存在着很强的耦合关系，所以日常检修计划通常与运用计划协同优化制定。但是动车组的高级修修时较长，在存在用车长高峰时期且检修能力有限的条件下，高级修送修计划需要提前制定。编制动车组高级修计划是以动车组的历史运用数据与检修记录为基础，结合检修规程、不同时期不同车型的用车需求以及有限的检修能力等因素来确定具体的送修时间。由于高级修计划是提前编制的，是动车组运用计划以及日常检修计划的前提条件，所以该计划在编制时无需考虑全年的动车组运用以及日常检修计划，只需将动车组的高级修率(处于高级检修状态的动车组列数占动车组保有量的比率)控制在给定的阈值之下，能为全年的各段时期(尤其是客流长高峰时期)提供预期数量的动车组即可。高级修计划编制完成后，根据高级修计划可以供应的车组数量以及实际的运输需求再实时制定动车组运用计划、日常检修计划以及检修基地的检修生产计划。编制高级修计划需重点考虑以下三方面。

1.1 高级修检修周期与检修等级

铁路动车组运用维修规程中部分动车组高级修检修周期见表1。

表1 CRH系列部分动车组高级修检修周期

由表1可见，四、五级修的检修周期长度分别为三级修检修周期长度的2倍和4倍。此外，动车组相邻两次高级修之间的间隔不能超过一个三级修的检修周期[1]。所以，动车组高级修的检修周期等于该型号动车组的三级修检修周期，只是相邻两次高级修的修程不同。根据这一规律可画出动车组高级修检修等级循环图,见图1。

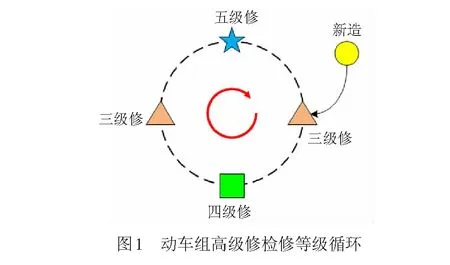
1.2 用车需求

我国铁路客流量主要集中在每年的春运、暑运、国庆节以及各小长假期间，其他时间较少。客流全年分布不均造成了不同时期动车组用车需求的不同。一个质量良好的高级修送修计划须满足各时期的用车需求。结合实际用车需求，本文在不同时期设置不同的高级修率上限来确保各时期的用车需求，如在客流高峰时期设置较低的高级修率，在客流低谷则相反。同时，根据实际需求，各型号动车组的在修列数也不能超过相应的上限值。

1.3 检修能力

本文是以“天”为最小单位时间进行计划的优化，且不涉及具体的检修流程，所以只需考虑各等级高级修每天的在修列数即可。此外，由于检修车间的能力限制，还应考虑一定的送车间隔。

2 优化模型

本文以动车组在本次高级修周期内的总损失里程最少为优化目标，考虑了检修规程、运车全年的用车需求以及检修能力等实际约束条件，建立0-1整数规划模型。由于动车组高级修送修计划每年编制一次，而高级修检修周期一般都大于1年，所以在目标计划期内同一列动车组至多检修一次。基于此本文假设在计划期内动车组至多进行一次高级修作业。而该模型构建的首要基础是生成动车组的备选送修时间集合，即送修时间窗。

2.1 备选送修时间集合生成策略

首先需要推算各动车组的高级修预计到修时间[10]。由于动车组高级修计划的编制不考虑动车组运用以及二级修计划，所以在推算预计到修时间时是以规划期内动车组的每天平均运行里程为依据进行的。推算出每列动车组的预计到修时间后，以其为中心生成动车组的送修时间窗。对于每列动车组来说，其时间窗在以“天”为最小时间单位时是连续的，所以可以用一个时间区间表示。推算动车组高级修预计到修时间需要准备的数据见表2。

此处以某一列动车组为例进行预计到修时间的推算，涉及符号定义见表2。

表2 符号定义

我们可以得到动车组距上次高级修的运行里程

( 1 )

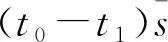
动车组的高级修送修日期推算公式为

( 2 )

式( 2 )中，动车组的预计到修日期以里程周期和时间周期中的先到者为准。在推算出预计到修日期之后，以预计到修日期为中心，检修周期的浮动区间为范围生成动车组高级修备选送修时间集合。具体步骤为

Step1准备动车组集E和空集E′。

Step2从集E中任意取出一组动车e，并按照式( 1 )与式( 2 )推算动车组预计到修时间t。

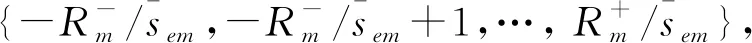
Step6若E为空，转Step7，否则转Step2继续执行Step2到Step6。

Step7令E=E′，输出所有动车组的送修时间集We(e∈E)，算法结束。

有时送修时间窗内的备选时间无法满足模型求解的需要，可适当扩大时间窗，但窗口的扩大会增加模型的求解难度。

2.2 数学优化模型

确定每列动车组的送修时间窗后，定义以下三组0-1决策变量为

模型中使用的集、角标和参数定义见表3。

表3 模型中使用的集、下标和参数定义

模型的目标函数是以动车组的损失里程(检修周期上限与该周期内的实际运行里程之差)最小为优化目标。最小化损失里程，可以增大相邻两次高级修之间的间隔，从而减少检修次数。对于各次高级修的检修成本，本文根据检修等级将其视为定值，不予考虑。因此，最小化损失里程可以实现高级修成本的最小化。模型构造

( 3 )

( 4 )

( 5 )

( 6 )

( 7 )

( 8 )

k∈[WSe,WEe] ∀e∈Em∈Mg∈G

( 9 )

∀g∈Ge∈Em∈M

(10)

k∈[WSe,WEe] ∀e∈Em∈Mg∈G

(11)

(12)

∀e∈Em∈Mg∈Gt∈T

(13)

各约束条件所代表的实际意义如下：式( 4 )保证了每列动车组在时间窗中只能选一个时间送修；式( 5 )保证了在不同时间处于高级修状态的动车组标准列数低于给定的高级修率上限值与保有量之积；式( 6 )保证了不同时间任意车型的在修车列数不超过在修列数的上限值；式( 7 )保证了在计划期内处于检修状态的动车组列数不超过对应等级的最大检修能力；式( 8 )保证了在计划期内检修车间可同时接收动车组的组数；式( 9 )保证了检修的完整性，即一旦检修工作开始就不能停下直到检修结束；式(10)保证了动车组处于高级修状态的范围；式(11)保证了送修间隔连续性；式(12)保证了检修车间处于送修间隔的范围；式(13)是决策变量的取值。

3 求解算法设计

对于配属动车组列数较多的铁路局集团有限公司，数学模型求解的复杂度较高，若应用传统的运筹学最优化方法求解，很难在可接受的时间内得到优化解。对此，本文结合该模型特点，采用具有求解精度高且寻优速度快的粒子群算法[16]进行优化求解。

3.1 模型约束条件的处理

在应用粒子群算法求解之前，需要对模型的约束条件进行处理。式( 4 )、式( 9 )～式(12)是逻辑约束，可以通过设定解的编码规则予以实现，另外4组约束可通过惩罚函数法进行无约束处理，从而可将模型转化为无约束的最优化问题。

对于惩罚系数的取值，一方面需要结合动车组的实际运用情况，另一方面则根据约束的强度不同进行确定。令λ1、λ2、λ3、λ4为式( 5 )～式( 8 )的惩罚系数，其中式( 6 )的约束最强，式( 7 )最弱，惩罚系数的大小关系为λ2>λ1>λ4>λ3。则模型的目标函数可转化为

(14)

3.2 粒子群算法相关策略

(1) 粒子编码方式及初始解生成

每个粒子表示各动车组送修时间的一个整体方案，根据式( 4 )，可将粒子的维度取为动车组的总列数，粒子中各维的取值依次等于对应动车组的送修时间，具体形式

Ti=(ti1,ti2,…,tie,…,ti|E|)

i=1,2,…,Ie∈E

(15)

式中：tie为第i个粒子中第e列动车组的送修时间；I为粒子群规模；|E|为动车组的总列数。

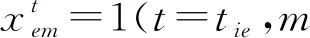
针对任意粒子中的每一维度(动车组e)的取值，通过在[WSe,WEe]内随机选取送修时间来确定，从而产生初始解。

(2) 惯性权重

为了使粒子群算法在进化早期具有较好的搜索能力而在进化后期具有较好的开发能力，本文采用线性时变惯性权重

ω(r)=ωmax-(ωmax-ωmin)r/Rmax

(16)

式中：ω(r)为第r次迭代时惯性权重的取值；ωmax、ωmin分别为惯性权重的最大值、最小值；Rmax为最大迭代次数。

(3) 学习因子

同样，为了使粒子群在前期加强全局搜索，在后期收敛于全局最优，本文通过不断减小自我学习因子和增大社会学习因子来实现，其变化方程

(17)

(18)

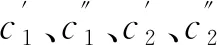
(4) 粒子进化方程

粒子以一定的速度(Vi)进行搜索进化，速度变量表示粒子位置的改变方向与改变量的大小，与粒子具有相同维度，则粒子的位置与速度的改变方程为

Vi(r+1)=ω(r)Vi(r)+c1(r)ξ(r)[Pi(r)-

Ti(r)]+c2(r)η(r)[G(r)-Ti(r)]

(19)

Ti(r+1)=Ti(r)+Vi(r+1)

(20)

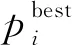
3.3 算法步骤

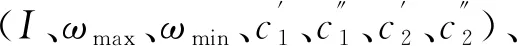
Step2计算各粒子的适应度值。

Step3对于每个粒子，比较其适应度值与其历史最优位置适应度值的大小，如果当前适应度更优，则更新粒子的历史最优位置。

Step4对于每个粒子，比较当前迭代次数的历史最优位置适应度值与全局最优位置适应度值的大小，如果某一粒子的历史最优位置的适应度值更优，则更新全局最优位置。

Step5根据式(12)～式(14)计算惯性权重、自我学习因子与社会学习因子。

Step6根据式(15)、式(16)更新粒子的位置与速度，更新过程中粒子的位置与速度均不允许超出给定的范围，若超出则取为边界值。

Step7r=r+1如果r>Rmax，转Step8，否则，转Step2。

Step8算法结束，输出计算结果。

4 案例分析

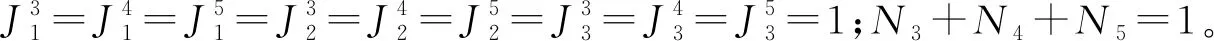
由于动车组实际数据保密而且非常复杂，所以这里只能给出经过加工的数据，即各动车组的送修时间窗。该集合是根据动车组运用与检修历史数据，调用3.1节所述方法所生成。为表示方便，可将备选日期用日期序数来表示(以数据统计日期为第1天)，如2017年1月1日用138表示。动车组的备选送修时间集合，见表4(只列出送修时间备选在计划编制期内的动车组，其中符号M1、M2、M3分别表示CRB1B、CRH1E、CRH380D车型)。

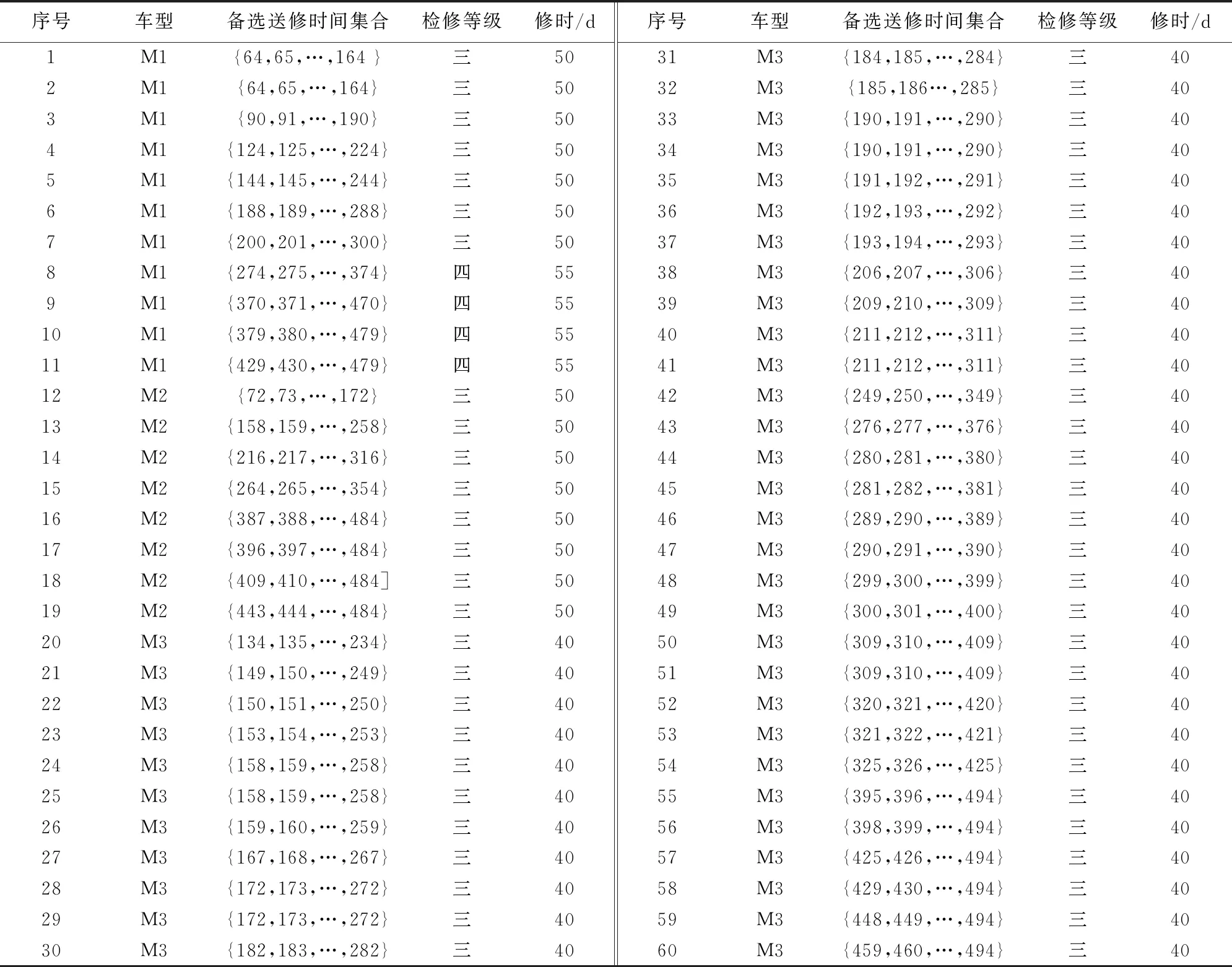
表4 动车组备选送修时间集合

由表4中可知，共有60列动车组在计划编制期内发生高级检修作业，其中送修时间最多的有101个备选日期，最少的只有36个备选日期。

此时，模型的目标函数可下式代替

(21)

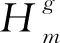
应用Visual Studio 2010开发平台，基于VC++语言，本文实现模型与算法的程序设计，计算环境为Intel处理器，2.00 GHz主频，4.00 GB内存。经试验，计算耗时为10 min左右，达到应用需求。求解迭代过程中的目标函数下降曲线见图2。

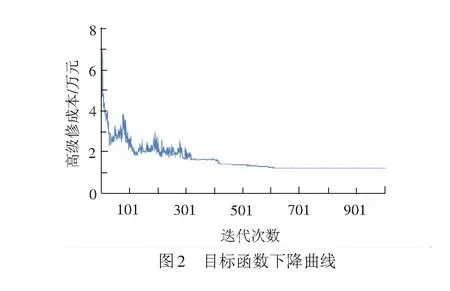
从图2可以看出，在前300次的迭代过程中，算法的搜索能力较强，可有效避免早熟现象的产生；而从第300次到第600次的迭代过程中，算法的开发能力变强，有利于最优解的寻找；最后400次迭代过程目标函数值没有变化，说明无约束问题的近似最优解已经生成。将求解结果进一步调整即可得到原问题的优化方案，调整策略如下：

Step1按照论文中式( 1 )与式( 2 )计算出参与高级修计划编制的动车组预计到修时间。

Step2将得到的松弛问题(近似)最优解中的相同型号动车组高级修送修时间按照Step1计算出的预计到修时间的顺序进行重排序。

Step3在计划期内逆向找到重排序后的方案中不满足原问题约束条件的最晚时间段(称为目标时间段)的起始时间和终止时间，并计算出目标时间段的跨度。

Step4将在目标时间段起始时间送修的动车组的送修时间在送修时间备选集的范围内向后移动，移动的长度是目标时间段跨度、送修时间备选集中最大值与计划送修时间之差两者之中的最小值。

Step5若无法后移，则将在目标时间段内在修的动车组的送修时间在送修时间备选集范围内向前移动。

Step6对调整后的方案按照原问题约束条件进行检查，重复Step3～ Step5，直到调整结果完全满足原问题的约束条件或者调整结果连续两次无改变为止。

最终方案见表5。

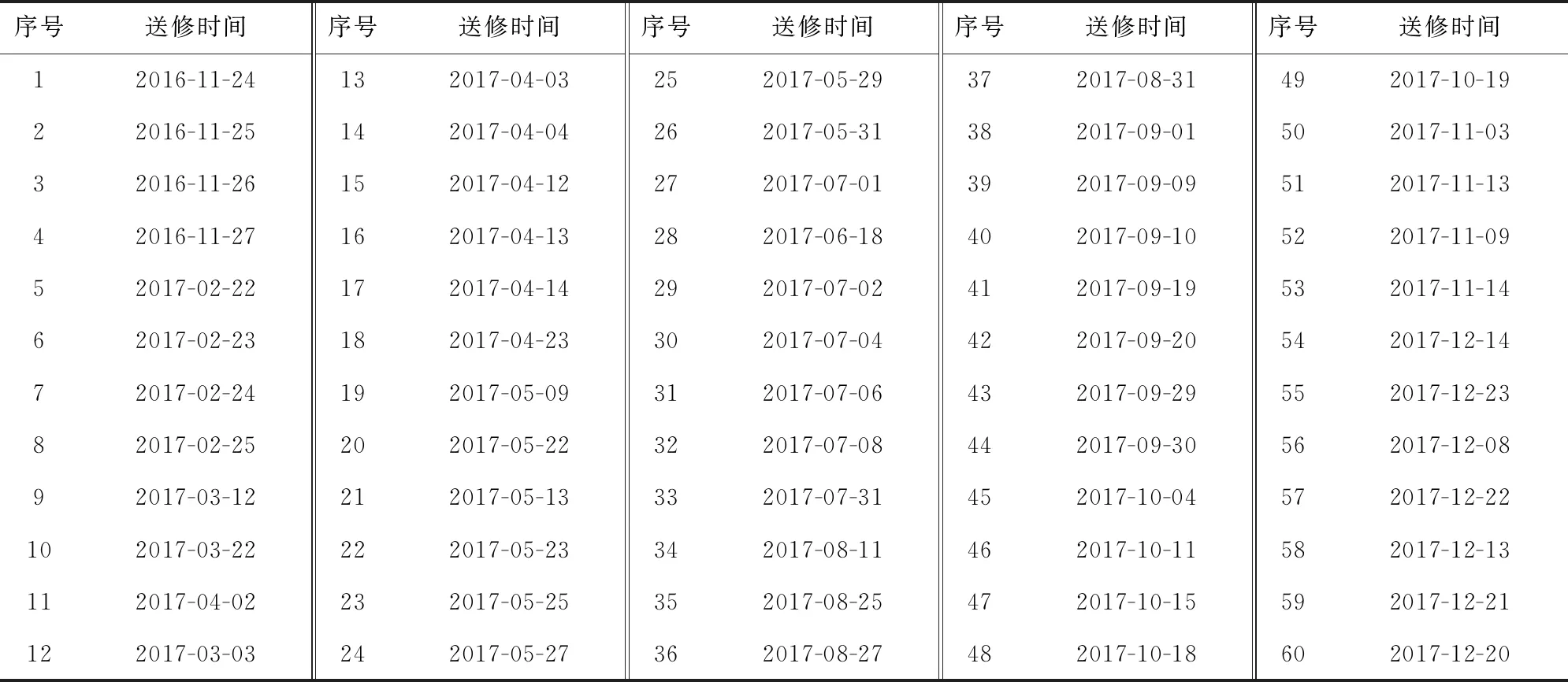
表5 动车组高级修送修时间表

根据优化方案和人工方案绘制高级修率折线图，见图3。

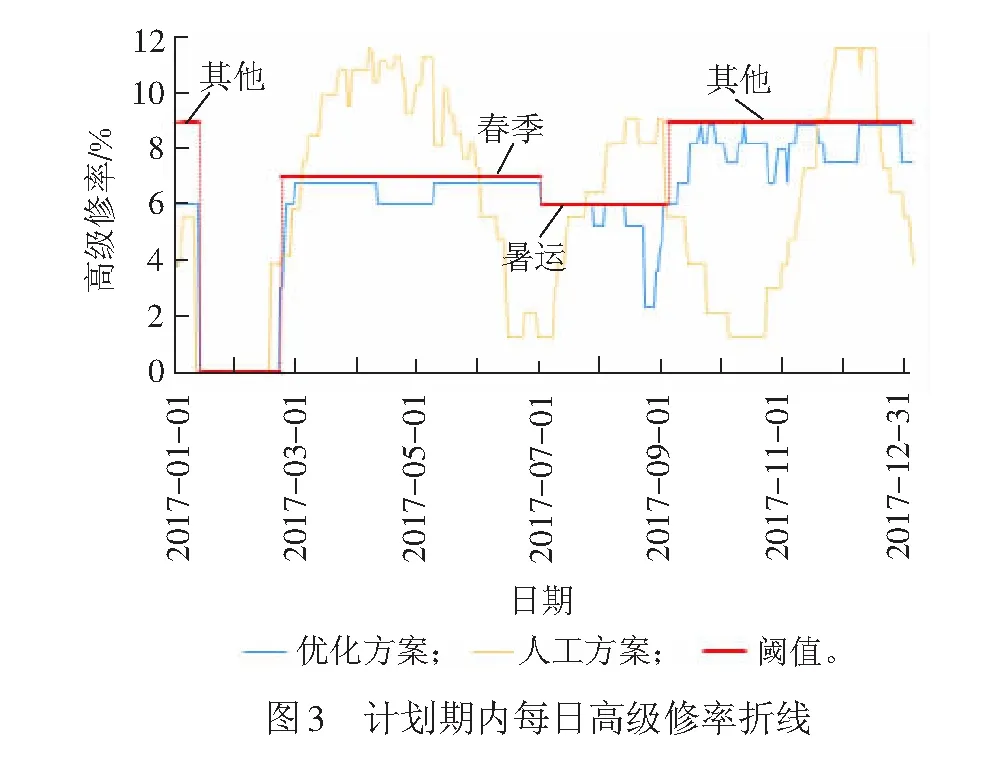
从图3可以看出，优化方案的高级修率在各时期都保持在上限值之下且变化平稳，满足用车需求，在计划执行时可轻微调整即可；而人工方案的高级修率偏离阈值较远且变化幅度大，在计划执行时需要不断的调整。将优化方法与人工编制方案相比，各指标见表6。

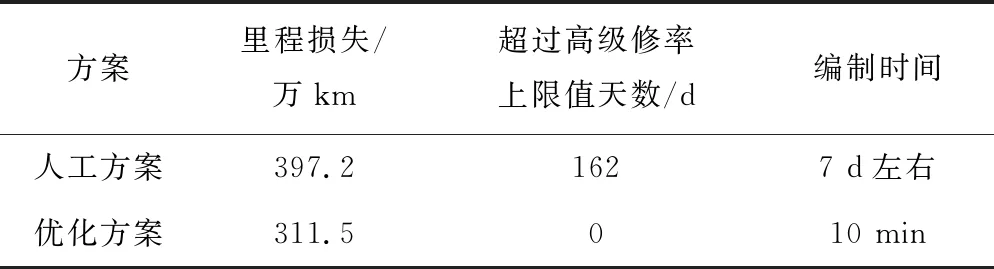
表6 不同方案各项指标对比

由表6可见，与人工方案相比，优化方案在里程损失、超过高级修率上限值天数和编制时间等方面都有优化。其中，损失里程从397.2万km减少到311.5万km，减少了85.7万km，减少百分比为21.58%；超过高级修率上限值天数从162 d降到0 d，可以更好地满足各时期的用车需求；计划编制时间从7 d左右减小到10 min，编制效率大大提升。

5 结束语

本文考虑了动车组高级修的检修周期、不同时期不同车型的用车需求以及检修能力限制等实际约束，以动车组损失里程最少为优化目标建立了0-1整数规划模型，并设计了相应的粒子群求解策略。最后通过案例分析说明了该方法的合理性与有效性。相对于人工编制计划，本文所述方法将动车组的损失里程降低了21.58%，将超过高级修率上限的天数从162 d降为0 d，将计划编制时间从7 d左右缩短到10 min，因此，本文所述方法提高了动车组高级修送修计划编制的质量和效率。但本文只是优化编制了配属于一个路局的动车组高级修送修计划，下一步需要从全路角度出发，优化全路的动车组高级修送修计划。