基于区域极点配置理论的高速列车速度估计

贾 超， 徐洪泽， 王龙生

(1.北京交通大学电子信息工程学院，北京 100044；2.中国铁道科学研究院通信信号研究所，北京 100081)

列车速度是设计列车自动驾驶控制策略，完成最优“速度-距离”曲线精确跟踪的前提。现行列车速度一般通过速度传感器获得，但传感器长期工作在恶劣的环境中，并需要承受由铁轨不平造成的强机械应力，容易产生故障进而引起列车故障，据日本有关方面曾统计，每半年就有9起因速度传感器问题而造成的机车故障[1]。相比之下，无速度传感器技术能够从容易测量的电机定子电压、电流等物理量中辨识出电机转速[2]，进而得到列车速度。这种技术降低了系统故障率，提高了控制单元的可靠性，节约了成本[3]，还可用于列车的速度监控及列车速度传感器故障诊断中[4]。目前，Adtranz公司将该技术应用于Helsinki的城市轻轨上[2]；西门子交通部在Boston和上海地铁三号线上应用了该技术，并与德国鲁尔大学联合开发的应用于更大功率的无速度传感器控制装置在西班牙地铁EMU已经通过测试[3]；日本5000型和8800型动车组也已经应用该技术[5]。

近年来，无速度传感器技术中的自适应速度观测器法(如降阶状态观测器法[6]、扩展卡尔曼滤波法[7]、滑模观测器法[8]、全阶磁链观测法[9-13]等)被广泛用于电机转速辨识中。其中，全阶磁链观测器法的观测精度高，避免了纯积分问题，在极点配置合理的情况下，能够保证误差矢量动态特性渐进稳定和误差矢量快速收敛到零，因此，该方法被大量用于无速度传感器控制技术中[14]。通常，为了使观测器收敛速度比电机模型快，一般将观测器极点配置在电机模型左侧kc倍位置。文献[9]设计了速度自适应磁链观测器，用于辨识感应电机转速，并令kc=1，即观测器极点与电机模型极点一致，这将造成系统在低速区域不稳定，因此，作者在文献[10]中将观测器进行线性化处理并增加了转速项，利用劳斯稳定判据，得到能够保证系统稳定kc的取值范围。文献[11]根据超稳定理论，提出转速估计自适应律，并令kc=1.2。文献[12]利用劳斯稳定判据分析出转速估计系统在低速再生制动区域不稳定，并给出了保证系统稳定的充要条件。文献[13]中，基于该充要条件设计了一种新型磁链观测器，将系统的不稳定区域缩减至一条直线。此外，受温度、集肤效应、磁饱和及电机运行频率等因素的影响，电机参数变化范围较大，这将影响电机转速辨识精度，而定子电阻的不匹配对转速估计精度影响最大[13]，为了提高转速辨识精度，文献[9，11]引入了参数辨识环节，用于辨识电机定子、转子电阻。然而，引入参数辨识环节以减小电机参数对转速辨识精度的影响，增加了系统的复杂程度；同时，精确配置观测器极点限制了观测器的收敛速度，降低了系统的鲁棒性，很难满足工程中多种性能指标需同时满足的实际需求[15]。

本文针对上述两个问题，基于区域极点配置理论，设计了具有一定自由度的全阶磁链观测器增益矩阵，依据Lyapunov稳定性理论推导出电机转速自适应律，提出了高速列车速度估计算法。本文采用区域极点配置理论设计观测器增益矩阵，提高了速度估计系统的鲁棒性。同时，本文所提算法在不增加系统结构复杂性的前提下，能保证存在不确定电机参数的速度估计系统的稳定性及列车速度的估计精度。

1 牵引电机模型

以CRH3型动车组列车为例，该动车组列车配有16台四极三相鼠笼式异步牵引电机。在两相静止坐标系下，以定子电流和定子磁链为状态变量，牵引电机标称模型可以表示为[16]

( 1 )

式中：

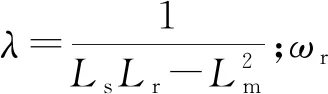
式( 1 )中，系统矩阵Am包含电阻参数Rs、Rr，电感参数Ls、Lr、Lm及转子角速度ωr等参数。而牵引电机在运行过程中，电机参数通常是未知且时变的，同时受温度、集肤效应及磁饱和程度等因素影响，电机参数通常会偏离其标称值。故需要对电机标称模型式( 1 )进行修正，将电机参数在标称值的基础上增加不确定项ΔRs、ΔRr、Δωr、ΔLs、ΔLr及ΔLm。则牵引电机实际模型表示为

( 2 )

式中：

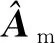
不确定参数矩阵ΔAm为

ΔAm=LMN

( 3 )

式中：L∈Rn×s，N∈Rt×n(s≤n=4，t≤n=4)为不确定性结构矩阵，不确定性系数M属于集合

X={M∈Rs×t|MTM≤It×t}

( 4 )

2 全阶磁链观测器

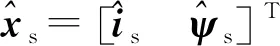
( 5 )

根据式( 5 )和式( 2 )，则实际状态估计误差系统为

( 6 )

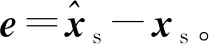
2.1 圆形区域D(c，r)

假设牵引电机模型的所有极点为

si=σi+jΩii=1，2，3，4

( 7 )

将观测器极点配置在电机模型左侧kc倍(kc≥1)位置。同时为了保证观测器在离散化后的稳定性，连续观测器的所有极点均需位于s平面左侧的圆形区域D(c，r)内，该圆形区域设计为

( 8 )

式中：i=1，3；T为采用周期，其取值范围为

( 9 )

由于kc≥1，故

(10)

(11)

式中：T≤Tc。圆形区域D(c，r)见图1。

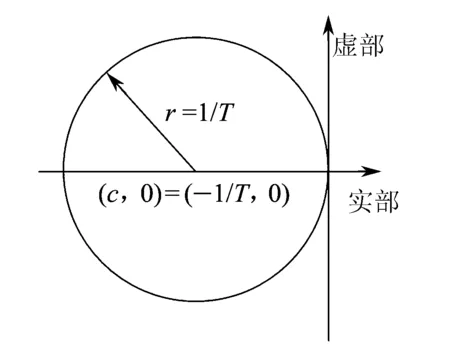
图1 圆形区域D(c，r)

2.2 观测器增益矩阵G

为了简化证明，引入如下记号

Ama=(Am-cI)/rCmr=Cm/r

(12)

(13)

Amae=(Am+GCm-cI)/r

(14)

ΔAmae=ΔAm/r=LrMNr

(15)

现设计反馈观测增益矩阵G使得对于一切容许不确定性M∈X，观测器的所有极点(即实际状态估计误差系统式( 6 )的极点)都被配置在圆形区域D(c，r)内。则G可以表示为

G=[G1G2]T=[g1I+g2Jg3I+g4J]T=

(16)

式中：P∈Rn×n为对称正定矩阵，对于一切不确定性M∈X，满足

(Amae+ΔAmae)TP(Amae+ΔAmae)-P<0

(17)

(18)

式中：R为适维对阵正定矩阵；ε>0[15]。

3 列车速度估计及对电机参数敏感性

3.1 列车速度估计算法

本文所采用的区域极点配置理论对电机参数变化具有较强的鲁棒性，同时电机参数的在线辨识会增加系统的复杂程度和在线计算量，不利于工程应用。所以，本文在进行速度辨识时，不考虑除转速之外其他变化的电机参数，牵引电机全阶磁链观测器可修改为

(19)

式中：

采用四阶龙格-库塔方法对该观测器进行离散化处理，得

(20)

式中：

根据式(19)和式( 1 )，状态估计误差系统为

(21)

定理1如果观测器增益矩阵G(式(16))用于状态估计误差系统(式(21))中，则式(22)成立。

(22)

证明：根据矩阵的Schur补性质，式(17)等价于，存在正定矩阵P∈Rn×n，对于一切不确定性M∈X和ξ∈R2n，使得式(23)成立。

ξ<0

(23)

可以表示为

(24)

对于所有满足[0Cmr]ξ=0的ξ≠0，有

(25)

即

(26)

根据文献[15]引理4，对所有满足[0Cmr]ξ=0的ξ≠0，有

(27)

由文献[15]引理2，对所有满足[0Cmr]ξ=0的ξ≠0，存在ε>0，使得

(28)

再根据文献[15]引理3，存在正定矩阵R-1，使得

(29)

则式(30)成立

(30)

即

(31)

由矩阵的Schur补性质，式(31)蕴含

(32)

则存在正定矩阵Q′，使得

(33)

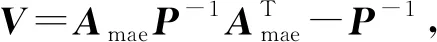
(34)

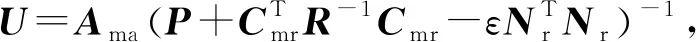
(35)

根据式(12)和式(14)，有

Amae=(Ama+GCmr)

(36)

将式(35)和式(36)代入式(34)的第一项，有

(37)

式(34)的第三项可表示为

(38)

将式(37)和式(38)代入式(34)中，并根据式(18)得

(39)

即

(40)

等价于

(41)

即

(42)

根据文献[15]引理1，存在正定矩阵P∈Rn×n使得式(42)成立，则表示矩阵Am+GCm的所有特征根均位于圆形区域D(c，r)内，即式(43)成立。

eig(Am+GCm)≤0

(43)

故定理1中式(22)成立，证毕。

定义Lyapunov函数为

(44)

式中：λ1为正的常数。

对Lyapunov函数求导，并根据假设1，得

(45)

定理1已证明式(45)右侧第一项为半负定矩阵，当满足

(46)

式(45)右侧最后两项之和为0，即V1>0，dV1/dt≤0，满足Lyapunov稳定性理论，即保证了转速估计系统的稳定性，式(46)即为电机转速辨识自适应律，为满足辨识的快速性，采用比例积分自适应律，表示为

(47)

对式(47)进行离散化处理，得

(48)

式中：

由于列车的速度与电机转速成正比，故可以在获得电机角速度(式(48))的基础上，根据电机角速度与转速的关系计算电机转速，再根据列车速度与电机转速的关系获得列车的估计速度，该过程描述为式(49)，即为列车速度估计律。

(49)

综上所述，高速列车的速度估计算法可描述如下：

算法1 高速列车速度估计算法

Step 2利用传感器测量列车当前时刻k牵引电机定子电流is(k)，定子电压us(k)。

Step 3将不确定参数矩阵ΔAm进行矩阵分解，确定矩阵L、N及不确定系数M；计算电机模型的所有极点，确定采样周期T，计算圆心c、半径r、kmax及圆形区域，并通过式(12)～式(15)分别计算Ama，Cmr，Lr，Nr，Amae，ΔAmae。

Step 4通过式(17)及式(18)，利用LMI工具箱求解正定矩阵P及ε，并根据式(16)计算观测器增益G。

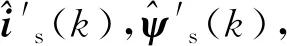
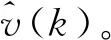
Step 7在下一时刻，即k=k+1时刻，重复Step2到Step6，直至结束。

列车速度估计的总体结构框图见图2。

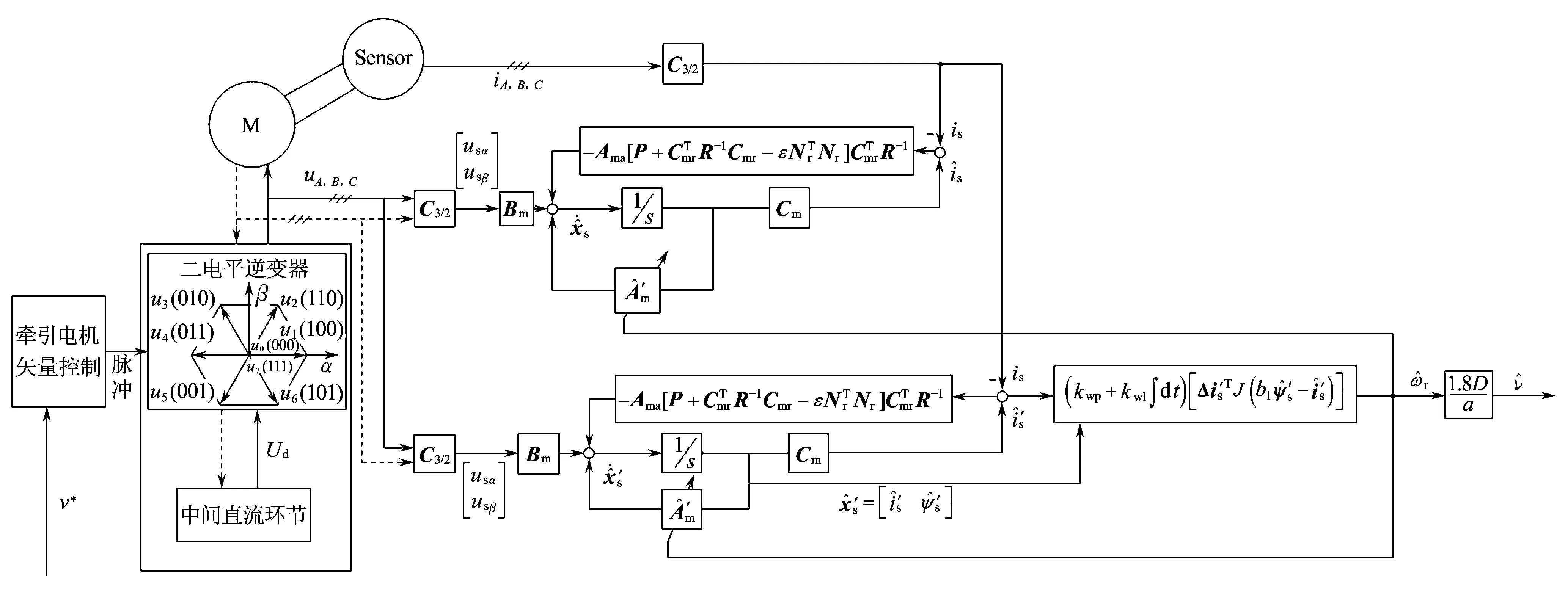
图2 列车速度估计系统总体结构框图

3.2 列车速度估计对电机参数敏感性

为了表达形式简单，在旋转坐标系下，将式( 1 )中状态方程及式( 5 )全阶磁链观测器方程表示为复矢量形式，分别为

(50)

(51)

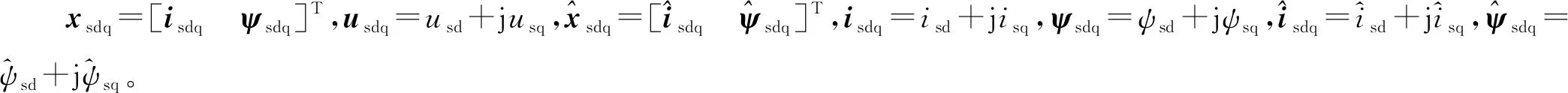
稳态时，可令d/dt(·)=0，推导出定子电流、定子电压及定子磁链矢量的稳态关系分别为

(52)

(53)

(54)

同时，将式(52)、式(53)代入式(51)，可以推导出定子电流观测矢量与定子磁链观测矢量的稳态关系为

(55)

式中：

q1(g2m1-g1n1)

b2=-(g2n1+g1m1)q1-p1(g2m1-g1n1)

m1(g4y1-g3x1)

b4=-(g4x1+g3y1)m1-n1(g4y1-g3x1)

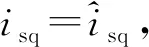
(56)

列车的估计速度因电机参数变化而造成的误差与电机参数的关系为

(57)

式中：v为列车实际速度。

利用Matlab仿真软件，绘制估计速度误差ev随电机的实际转速和负载变化的三维图，利用三维图分析电机参数变化对估计速度误差ev的影响。仿真选用CRH3型列车，列车总质量m=536 t，车轮直径D=0.92 m，列车牵引电机总数Nm=16，齿轮传动比a=2.788，传动效率η=0.975，基本运行阻力系数分别为c0=0.42，cv=0.001 6，ca=0.000 132。该车型的牵引电机参数为：额定功率Pm=560 kW，频率f=138 Hz，定子电阻Rs=0.106 5 Ω，转子电阻Rr=0.066 3 Ω，定子电感Ls=1.31 mH，转子电感Lr=1.93 mH，互感Lm=53.6 mH，极对数np=2。

令电机参数实际值与标称值相对误差为±50%，分别分析定子电阻、转子电阻、定子电感、转子电感及互感对估计速度误差的影响。选择电机转速变化范围为0～500 r/s，负载随列车速度变化而变化，具体为

(58)

式中：TL为牵引电机负载；fb为基本运行阻力，包括滚动阻力和气动阻力，表示为

fb=m(c0+cvv+cav2)

(59)

Am=

M=1×104

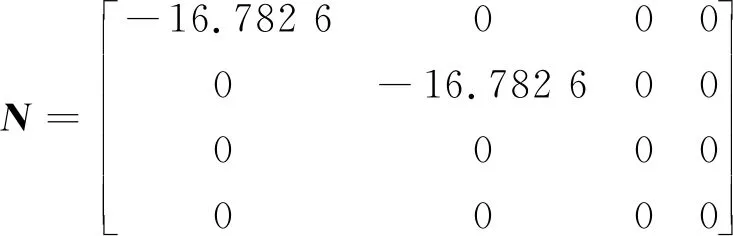
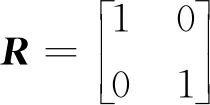
当ωr=1.5p.u.时，电机模型的极点分别为：(-20.59+648.8i)，(-20.59-648.8i)，(-50.42+1.51i)，(-50.42-1.51i)。利用式(10)，可得T≤9.77×10-5，令Tc=8×10-5，k=kmax=1.22，则圆形区域为：圆心为(c=-1.25×104，0)，半径为r=1.25×104m。根据仿真参数，求解对应的线性矩阵不等式式(17)及式(18)，则可得P及ε的可行解

P=

ε=2.35×104

观测器增益矩阵

根据上述参数，可得估计速度误差对定子电阻的敏感性三维图，见图3。其余参数变化对估计速度误差的影响分析过程与该过程一致，此处不再详细赘述，仿真结果见图4～图7。

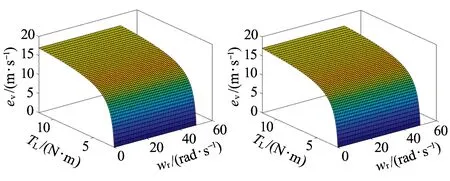
图3 速度估计误差对定子电阻的敏感性三维图

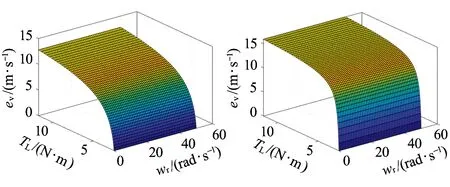
图4 速度估计误差对转子电阻的敏感性三维图

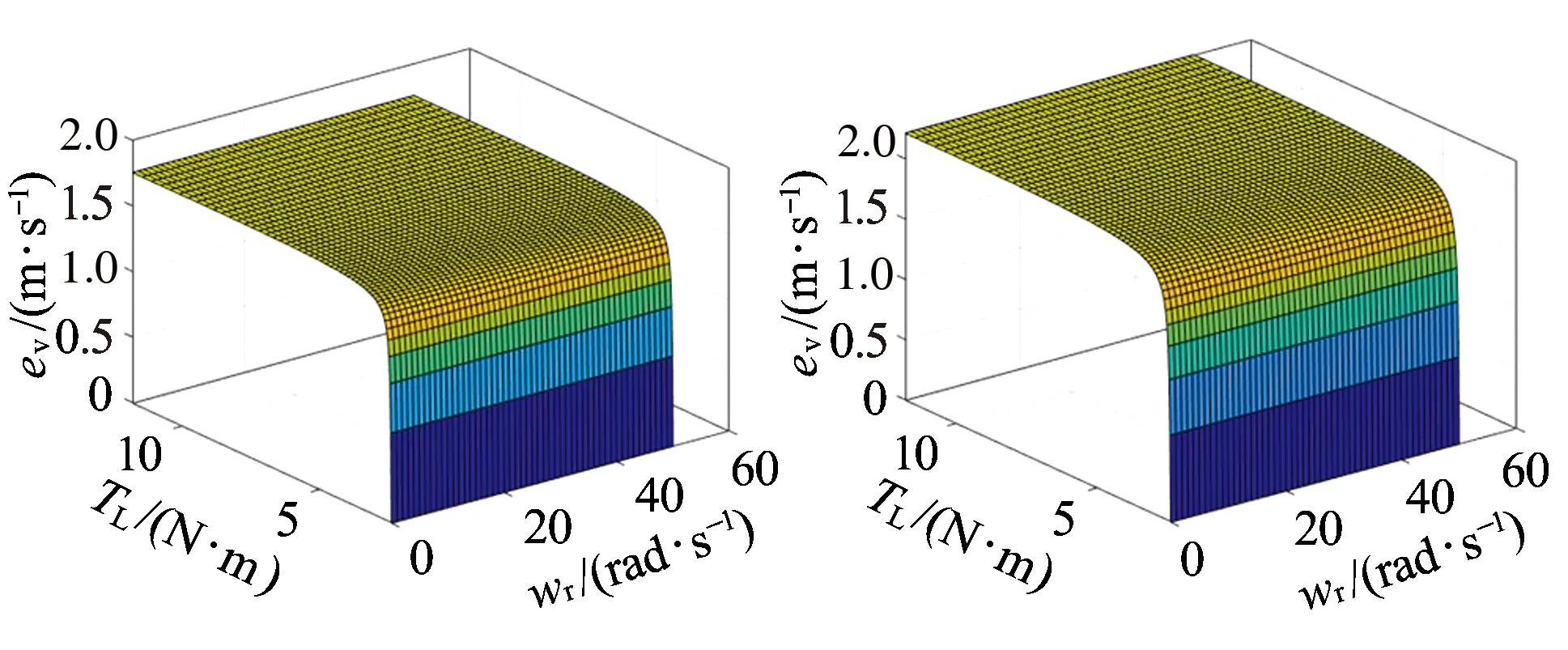
图5 速度估计误差对定子电感的敏感性三维图

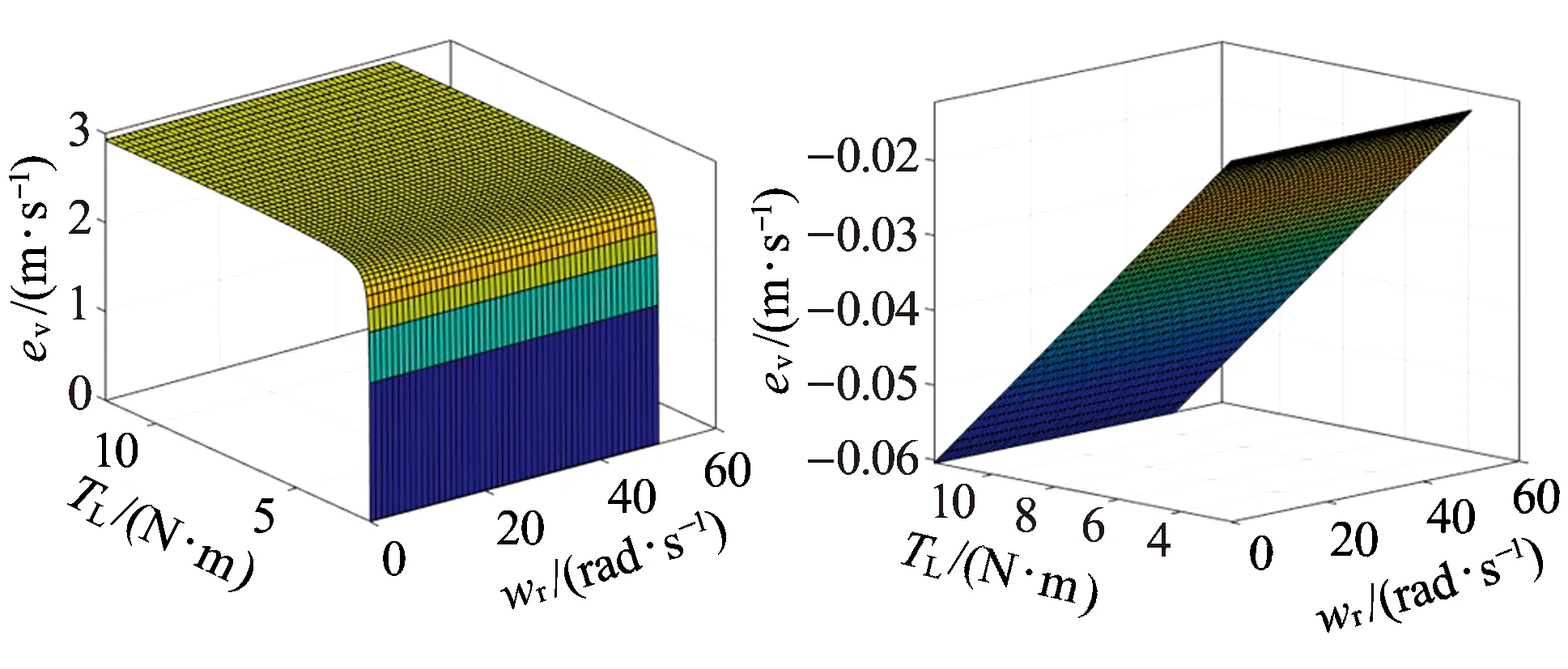
图6 速度估计误差对转子电感的敏感性三维图

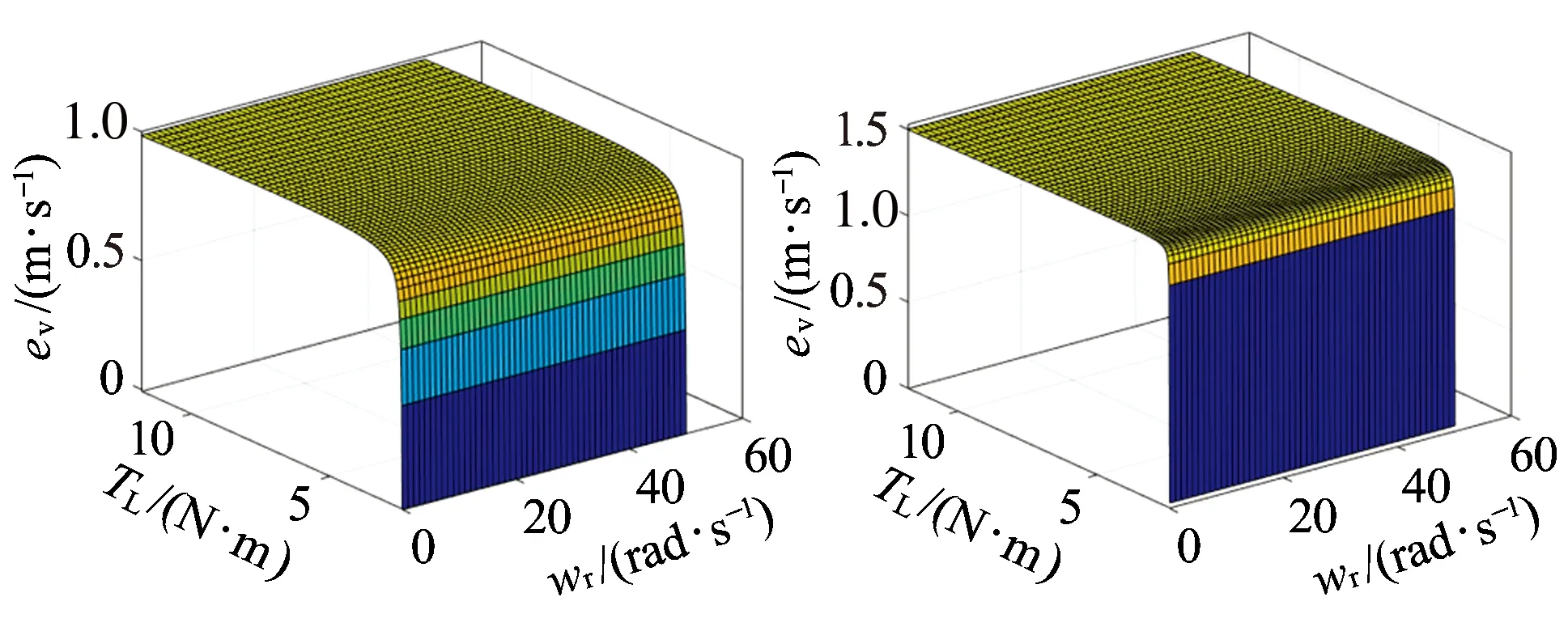
图7 速度估计误差对互感的敏感性三维图

从图3～图7可知，定子电阻变化对估计速度误差影响最大，转子电阻次之，这是因为定子磁链观测值与定子电阻直接相关，其他电机参数只会对定子电流观测值产生影响，侧面影响列车速度估计值。当转速一定时，随着负载的增大，估计速度误差值越大。此外，除转子电感外，其余几个电机参数的变化均会造成速度的估计值小于速度的实际值。

4 数值仿真

仿真具体参数见3.2节中参数，从3.2节所获结论可知，定子电阻变化对估计速度误差影响最大，转子电阻次之。故本节分别选择定、转子实际值小于标称值和大于标称值两个算例来证明本文所提列车速度估计算法的有效性。同时令列车的期望速度为：15 m/s(0～1 s)，70 m/s(1～2 s)，30 m/s(2～3 s)，3 m/s(3～4 s)。

4.1 算例1

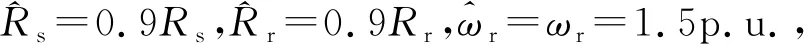
N=103×

当ωr=1.5p.u.时，电机模型的极点分别为：(-18.6+649.5i)，(-18.6-649.5i)，(-30.2+0.815i)，(-30.2-0.815i)。利用式(10)，可得T≤8.81×10-5，令Tc=8×10-5，则k≤1.1，取k=kmax=1.1。根据式(11)可得圆形区域D(c，r)：圆心为(c=-1.25×104，0)，半径为r=1.25×104m(图8黑色曲线)。从图8可知，当转速ωr从0变化到1.5p.u.时，观测器的所有极点均在圆形区域内。

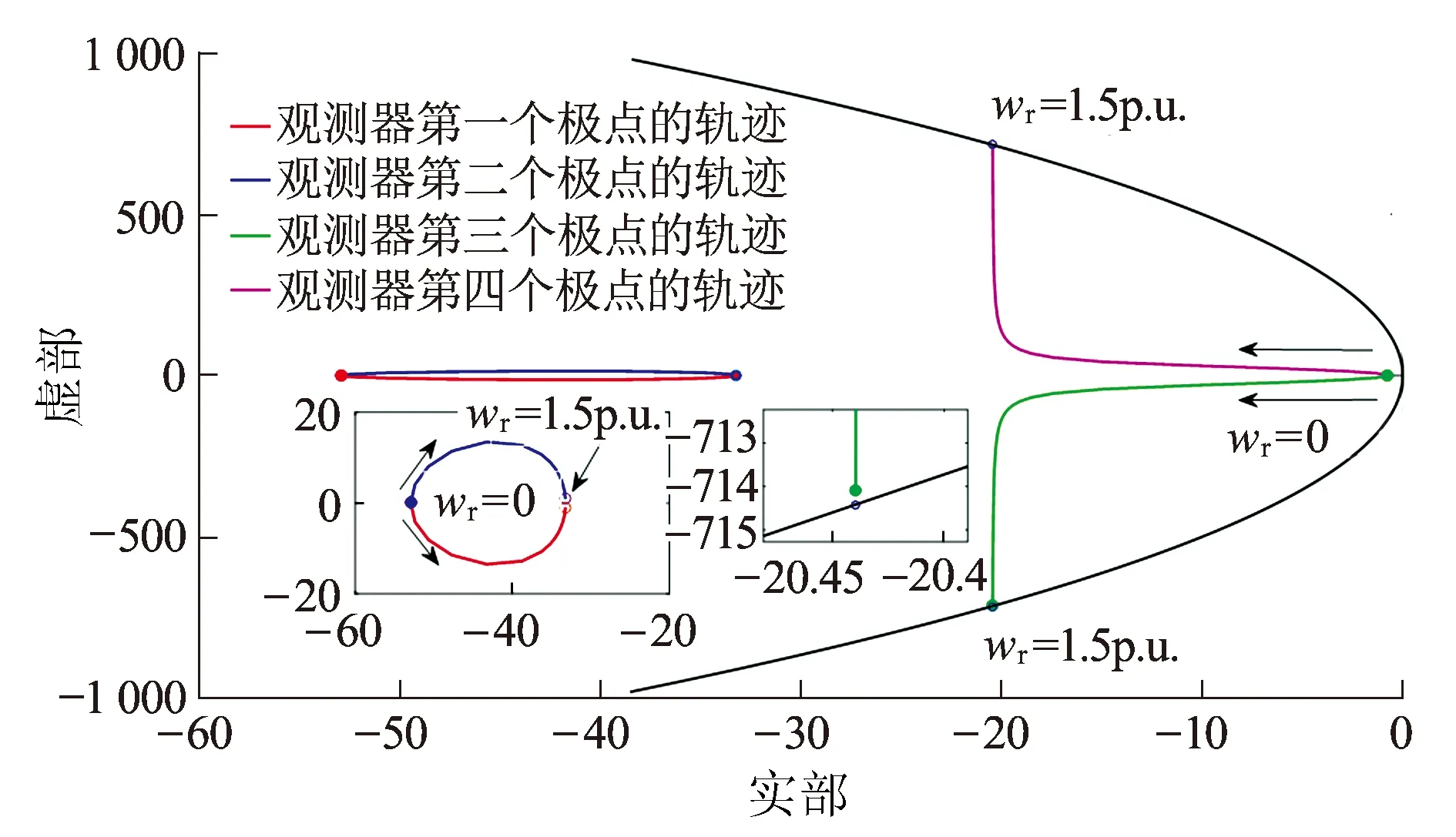
图8 观测器极点轨迹及圆形区域D(c，r)

根据仿真参数，求解对应的线性矩阵不等式，则可得P及ε的可行解为

P=10-6×

ε=2.62×10-11

仿真结果见图9，从图中可知，即使电机定子电阻、转子电阻存在10%的偏差，列车的估计速度与实际速度基本一致。

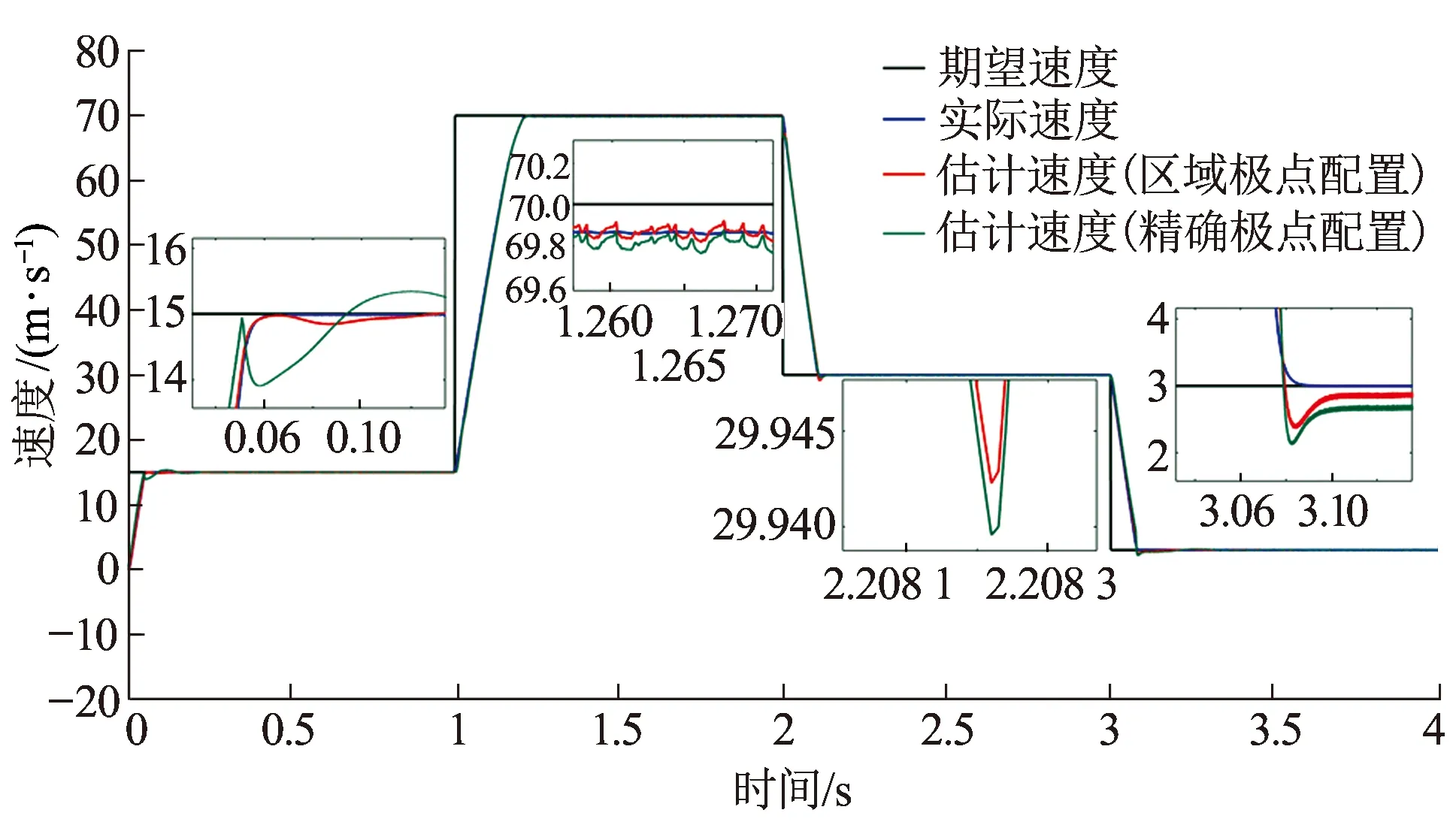
图9 算例1列车估计速度曲线

图10 算例1列车实际速度与估计速度偏差曲线

列车的实际速度与采用两种方法估计出的列车速度的偏差曲线见图10，偏差的平均值见表1，及各个时间段速度偏差满足|ev|≤0.1 m/s时所需时间。从图10及表1可知，本文所提算法(采用区域极点配置法)估计出的列车速度与传统的精确极点配置法估计出的速度相比，前者更接近列车实际速度。且在每一个时间段，经过0.3 s后，速度估计值均能够收敛至实际值，这表明转速估计系统是稳定的。此外，本文所提算法估计的列车速度偏差值满足|ev|≤0.1 m/s的时间与传统方法相比，前者时间更短。

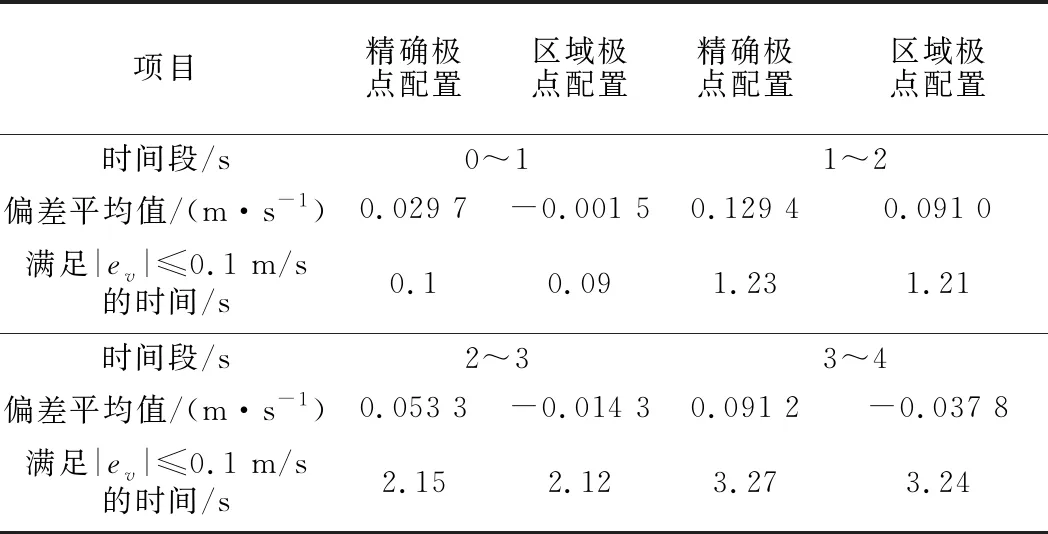
表1 算例1列车实际速度与估计速度的偏差值

算例1中电机的极点及观测器的极点见图11，从图11中可以看出，所有的观测器极点均在圆形区域内。

图11 算例1电机模型极点与观测器极点

4.2 算例2

ΔAm=

N=103×

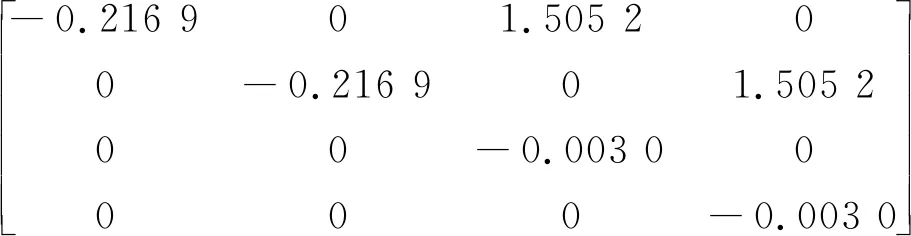
经过计算可得T≤1.47×10-4，令Tc=1×10-4，k=kmax=1.47，则圆形区域为：圆心为(c=-1×104，0)，半径为r=1×104m。线性矩阵不等式的可行解为

P=10-6×

仿真结果见图12，在电机定子、转子电阻偏离原始值50%的情况下，速度估计值与速度实际值基本一致。

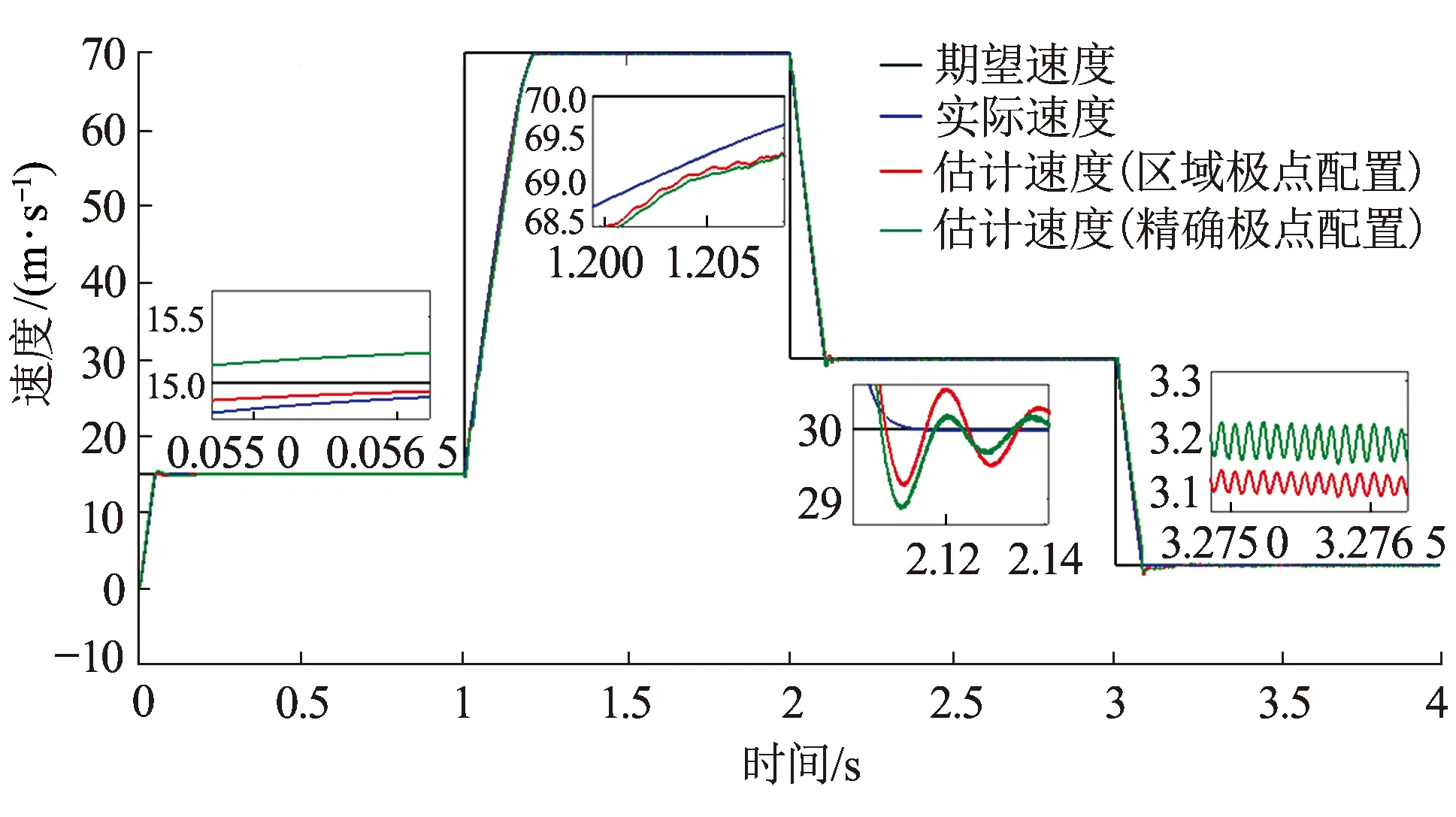
图12 算例2列车估计速度曲线

列车的实际速度与采用两种方法估计的列车速度的偏差曲线见图13，偏差的平均值见表2，及各个时间段，速度偏差满足|e|≤0.1 m/s时所需时间。从图13及表2可知，本文所提算法估计出的列车速度更接近列车实际速度。在每一个时间段，经过0.4 s后，速度估计值均能够收敛至实际值，这表明转速估计系统是稳定的。同时，本文所提算法估计的列车速度偏差值满足|ev|≤0.1 m/s的时间更短，尤其在时间段1～2 s和时间段2～3 s更为明显，这表明精确极点配置法在列车中、高速运行时，列车速度估计值收敛至实际值时间较长，且偏差相对较大，而本文所使用的方法在0.2 s后便能够满足与列车实际速度的偏差小于等于0.1 m/s。即本文所提算法鲁棒性更强，收敛速度更快。

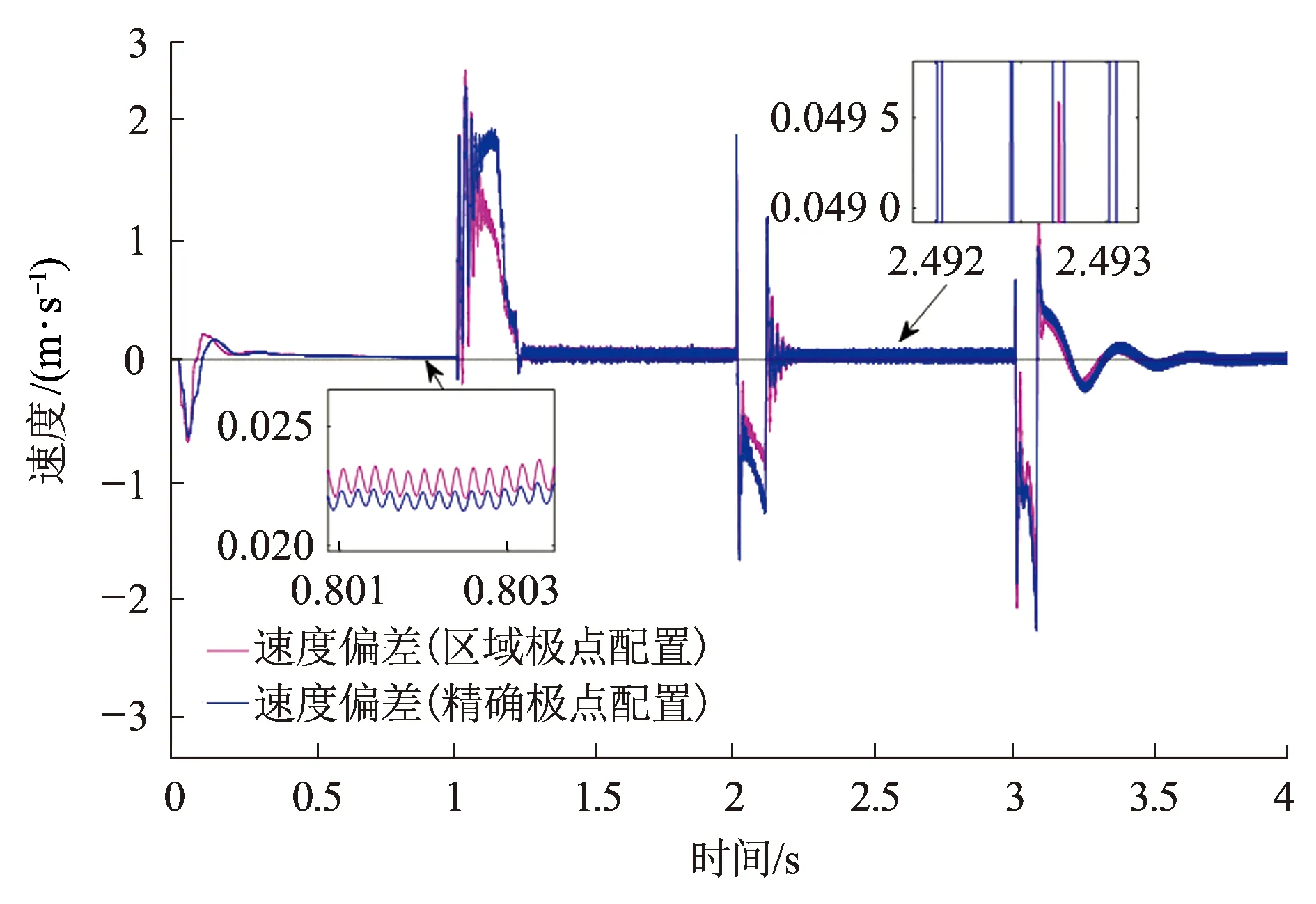
图13 算例2列车实际速度与估计速度偏差曲线

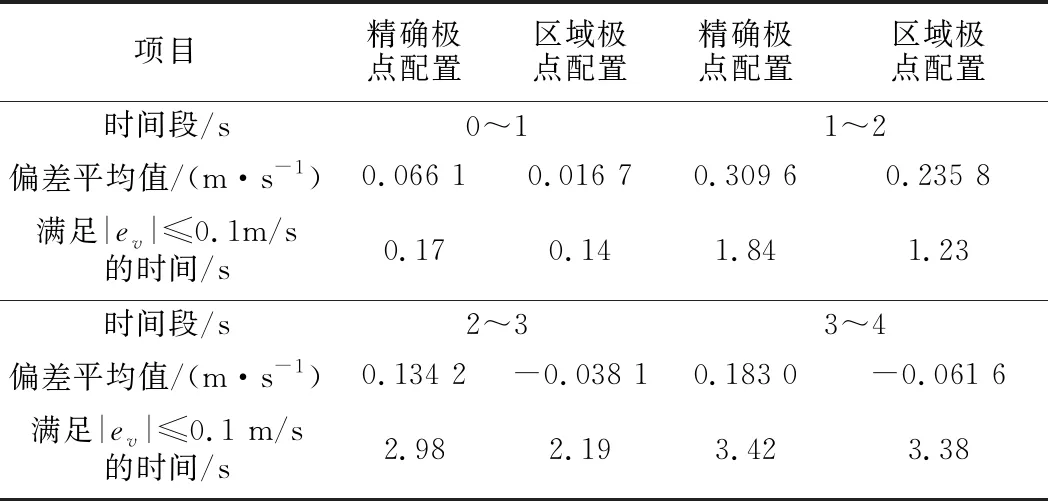
项目精确极点配置区域极点配置精确极点配置区域极点配置时间段/s0～11～2偏差平均值/(m·s-1)0.066 10.016 70.309 60.235 8满足|ev|≤0.1m/s的时间/s0.170.141.841.23时间段/s2～33～4偏差平均值/(m·s-1)0.134 2-0.038 10.183 0-0.061 6满足|ev|≤0.1 m/s的时间/s2.982.193.423.38

算例2中电机的极点及观测器的极点见图14，可以看出，所有的极点均在圆形区域内。

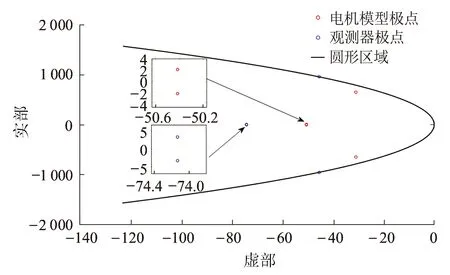
图14 算例2电机模型极点与观测器极点

从图9、图10、图12和图13可知，即使定子、转子电阻存在偏差的情况下，速度估计值均能收敛到速度实际值，从而验证了速度估计算法的有效性。且在电机定子、转子电阻偏差为50%时，本文所提算法仍能准确地估计出列车的速度，这表明本文所提算法具有较强的鲁棒性。此外，比较表1跟表2可知，定子电阻、转子电阻的实际值与理论值偏差越大，最后的速度估计误差就越大，满足速度偏差值|ev|≤0.1 m/s的时间更长。同时，与精确极点配置法相比，本文所提算法收敛速度更快，鲁棒性更强，估计出的列车速度与实际速度偏差更小。

5 结束语

本文采用无速度传感器技术的全阶磁链观测器法，基于区域极点配置理论，提出了高速列车速度估计算法，并给出了估计速度对电机参数变化的敏感性分析，分析结果为定子电阻变化对列车速度估计值影响最大，转子电阻次之。进而从定子、转子电阻取两组不同值的情况下进行仿真，并与传统精确极点配置法进行对比，验证了本文所提算法的有效性。结果表明，两种情况下，列车速度估计值均收敛于实际值，且在电机参数存在较大偏差的情况下，仍能准确估计出列车的速度，具有较强的鲁棒性，与传统精确极点配置法相比，本文所提算法鲁棒性更强，收敛速度更快。同时，本文所提算法能在不增加系统结构复杂性的前提下，保证存在不确定电机参数的列车速度估计系统的稳定性及列车估计速度的精度，可以降低系统的故障率，提高系统的可靠性及可维护性。