基于改进多色集合的动车组转向架系统故障传播模型研究

林 帅， 王艳辉， 贾利民， 李 阳

(1. 北京交通大学 轨道交通控制与安全国家重点实验室， 北京 100044；2. 北京交通大学 北京市城市交通信息智能感知与服务工程技术研究中心， 北京 100044; 3. 北京交通大学 交通运输学院，北京 100044)

动车组转向架系统作为高速列车的重要组成部分，是耦合高度复杂、功能丰富、运行控制能力强大的复杂机电系统[1]。鉴于系统中部件间紧密耦合与协调工作机制，任意部件失效不仅会引起该部件自身故障，并且会通过部件间相互依赖的关系影响其他部件的运行状态，进而导致整个系统出现异常。因此，从部件的故障传播分析入手，研究面向全局系统故障扩散过程对于保障高速列车系统安全稳定运行具有重要的现实意义[2]。

现有的关于系统故障传播建模及分析方法大致可分成两类：

(1) 基于定性知识模型的方法。以由专家经验或故障数据所获取的定性描述和反映机理的深层次知识为基础，建立相应故障关联关系模型反映系统中故障因果关系及相互影响过程(如故障树[3-4]、失效模式影响和危害度分析法[5]、Petri网[6-7]、贝叶斯[8]、有向图[9-11]等)。该类方法是目前系统故障传播动力学行为研究中最常用的方法，但其致命缺陷在于所获取的作为构建故障传播模型基础的“知识”，通常人为影响因素较大，且模型完备性难以验证，建模过程与计算度复杂；其次模型中往往只针对部件主要失效模式进行概率设计，忽略部件多种失效模式间的相关性影响以及系统拓扑结构对故障传播的影响。

(2) 基于拓扑网络模型的方法。以系统拓扑结构为基础建立相应的表征系统全局拓扑结构的网络模型，按照分步扩散的原则结合网络理论提出故障扩散强度[12-14]，研究故障在网络中的传播过程，最后采用蚁群等算法计算整个网络中扩散能力最强的故障传播路径。它克服了以“经验知识”建模存在的缺陷，考虑了系统拓扑对故障传播的影响，但忽略了不同失效模式对故障传播广度和深度的影响以及部件间的功能依赖关系，并且该模型仅能分析整个网络中高风险路径，对不同部件失效可能的传播路径及相应路径的发生概率却无法获得。

针对上述基于拓扑网络模型的故障传播建模存在的问题，本文首先基于网络理论构建可用于描述动车组转向架系统内部耦合关系的全局拓扑网络模型，并以此为基础结合分步扩散机制提出由节点综合重要度和故障模式所确定的节点故障传播强度，研究单节点的故障传播过程。鉴于单节点故障传播并不能反映出系统故障扩散的随机性、不确定性以及复杂性，借鉴多色集合理论在进行矩阵间运算的优势，将原有多色集合理论中元素间仅有的0-1关系扩展至由概率所表征的耦合关系，提出基于节点故障扩散强度和改进多色集合理论的针对系统级的故障传播模型。最后应用于CRHX型动车组动车转向架系统的系统故障传播分析结果表明，该方法能够有效地找出系统中任意部件失效所有可能的传播路径及相应的发生概率，从而为系统故障维修与安全性分析提供理论支撑。

1 相关理论

1.1 系统全局拓扑网络模型

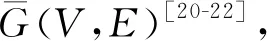
( 1 )

式中：V为网络中节点集合；vi∈V为网络中的节点；E为网络中边集合；eij∈E为网络中的边；f(V)为节点属性集合；f(E)为边属性集合；Fv为节点功能测度集；Tv是节点拓扑测度集；FM为故障模式集；Fe是边功能测度集。

1.2 多色集合理论

多色集合理论[26-27]是由俄罗斯Pavlov教授于1976年提出的一种新型系统理论和信息处理数学工具。其核心思想是使用多色集合理论表示性质的统一标准数学模型进行系统仿真，且这些性质不取决于仿真对象的内容。

传统集合A={a1,…,ai,…,an}中，ai∈A所不同的仅仅还是元素的名字，尽管这些元素是不同的，但他们的任何其他性质在形式上并没有表示出来。多色集合理论则是在传统集合的基础上，对整体集合A和各元素涂上一些不同的颜色，用来表示研究对象及其所包含的元素的性质。

若颜色集合F(ai)={f1,…,fi,…,fk}为元素ai的个人着色，其中fk为元素ai的第k个颜色，F(A)=(F1,…,Fi,…,Fk)为集合A的统一着色，Fk为多色集合的第k个统一颜色。多色集合理论中，应用布尔矩阵A×F(a)描述集合所有元素及其属性之间的关系，即

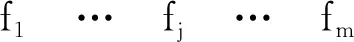
( 2 )

若集合A中的一个或多个元素ai∈A同时存在时统一颜色fj才存在，那么这些元素ai∈A组成的集合称为统一颜色Fj的个体，记为A(Fj)={ai,…,aj}，‖A(Fj)‖0为集合A中非零元素的个数。

鉴于篇幅限制，这里只介绍本文所用到的相关多色集合理论，更多的关于多色集合理论的研究请参考文献[26-27]。

2 节点故障扩散强度研究

转向架系统作为一个高度耦合的有机整体，任意部件的微小故障都有可能引起故障的传播最终导致系统功能失效。因此从微观角度研究节点故障扩散过程对于全局系统的故障传播是十分必要的。

2.1 节点综合重要度计算方法

重要度通常是用于度量系统部件/单元状态变化对系统性能的影响程度。传统的重要度如可靠性重要度、结构重要度、寿命重要度等[15-23]，仅考虑的是部件功能重要性，忽略了拓扑结构对部件关键程度的影响。因此，本文从维持全局系统结构和正常功能相结合的角度提出基于Choquet积分[24-25]的综合重要度FTI综合衡量部件对系统的影响。部件重要性的影响因素有很多种，各因素间并不是完全独立，相比于传统的黎曼积分，Choquet积分在融合多影响因素的过程中考虑了各影响因素间的耦合关系。其具体构建步骤为

Step1构建动车组转向架系统全局拓扑网络模型G(V,E,f(V),f(E))，确定节点和边的属性测度集中的元素。

Step2计算Step1中所确定的节点拓扑测度集Tv，包括度di、介数bi、紧密度ci等；节点功能测度集Fv，包括故障概率λi、平均无故障时间MTBFi等；以及边功能测度集Fe，包括连接强度stij、故障传播概率pij等。

Step3在原有节点拓扑测度定义的基础上，利用Choquet积分融合节点和边功能测度扩展原有定义形成节点广义重要性测度，其普适性数学表达式为

i=1,…,mt=1,…,N

( 3 )

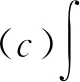
其中,

Step4再次利用Choquet积分将所构建的多种广义重要性测度聚合构建节点FTI，即若节点vi的广义重要性测度集GIMi={Ii1,Ii2,…,Iim}，其中Iim为节点vi的第m个广义重要性测度，则节点vi的FTIi为

( 4 )

式中：Iij为部件vi的第j个广义重要性测度值；μ(Ii)为各评价测度的权重且Ii=(Ii1,…,Ii(N))，Ii1≤…≤Ii(N)；m为广义重要性测度的个数。

2.2 节点故障扩散强度

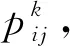
( 5 )

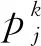
3 基于改进多色集合的系统故障传播模型

上文中研究了基于单节点的故障扩散过程，但对于动车组转向架系统而言，故障传播过程具有随机性与不确定性，传播路径的选择也具有多样性与复杂性。因此，本节从全局系统角度提出基于改进多色集合的针对系统级的故障传播模型。

3.1 改进多色集合理论

与传统的集合论相比，多色集合的属性模型能够方便地描绘转向架系统中各种特征和特征间的相互关系；与Petri网相比，其为矩阵间的运算，计算机编程实现难度降低，普适性更强。而系统故障传播具有并发性、多样性与随机性，以矩阵间运算描述传播过程具有显著优势，因此这里选取多色集合理论用于表征系统级的故障传播过程。

多色集合理论中，通常用0-1布尔矩阵表征个人颜色与统一颜色的关系。但实际上个人颜色也是不同的，因此对其进行改进，若个人颜色fi影响到统一颜色Fj的存在，则cij为个人颜色fi的取值，即

‖cij‖F(a),F(A)=〈F(a)×F(A)〉=

( 6 )

在故障传播过程中，受复杂多变的运行工况影响，一个节点的故障导致网络中其他节点故障往往具有一定的概率性，不能用0或1表示。因此改进后的多色集合理论更适合于故障传播动力学行为的研究。

3.2 故障传播模型构建

3.2.1 故障模式相关矩阵

部件的故障模式在一定程度上反映了部件失效的程度，严重的故障模式将增加故障扩散强度。不同部件的不同故障模式之间存在相互关联关系，本文采用表1所示的5个等级自然语言值表示故障相关度[18]。

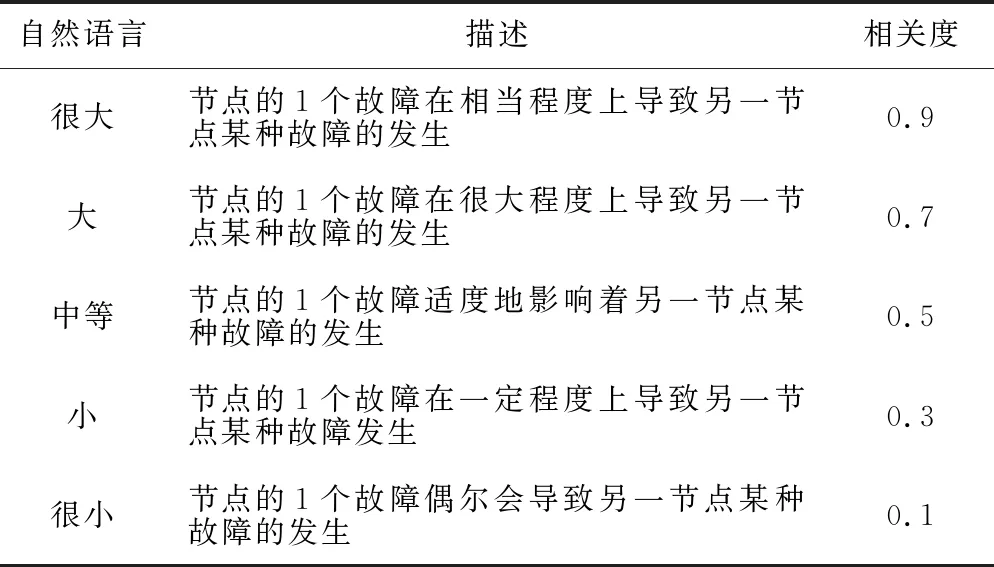
表1 故障模式相关矩阵评分标准

由表1可得到动车组转向架系统全局拓扑网络中各节点的故障模式相关矩阵为

( 7 )

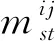
3.2.2 故障传播模型

为了清晰、简洁地表示系统的故障传播机理，这里利用在描述矩阵间运算具有优势的改进多色集合理论推理系统级故障传播可能的路径及各路径的发生概率。借鉴文献[28]首先定义2个特殊算子：

(1) 直乘算子＊。若A=[aij]m×n，b为n维列向量，则C=A＊b=[aijbi]m×n。

(2) 乘法算子⊗。若A=[aij]m×n，b为n维行向量，则C=A⊗b=[aijbj]m×n。

依据式( 5 )将其用矩阵形式描述，则k步扩散后，故障传播模型为

Mk=[M(i)]k=Mk-1(i)+

{wpPk(i)+wsTk(i)}⊗Fk(i)

( 8 )

其中,

Pk(i)=〈V,A((Rk-1(i)p(E))＊p(V))〉T

Tk(i)=〈A(Rk(i)),I〉

Fk(i)=

i=1,…,‖Rk-1‖0j=1,…,‖Rk‖0

式中：Mk为第k步传播后系统故障路径集；[M(i)]k为第k步传播后第i条路径上各节点状态；Rk(i)仅为第k步传播时第i条路径上发生故障的节点状态；A[(Rk-1(i)p(E))＊p(V)]为第k步传播时第i条路径上故障的节点集合；Tk(i)为第k步传播时第i条路径上故障节点的综合重要度；Fk(i)为第k步传播时第i条路径上故障节点最可能发生的故障模式；D(Rk-1(i))为表示第k-1步传播后第i条路径上故障节点的编号；fmDk-1,u为第k-1步传播时节点Dk-1的第u种故障模式。

若从能量的角度来看，部件自身故障前内部不断有能量的累积，能量密度不断增大，当累积的能量超过该部件的最大容量时故障即发生。这里给出故障传播停止的2个阈值条件：

(1) 节点之间的故障扩散强度随传播路径长度的增大成数量级减小，当扩散强度低于10-8时，则该节点处于安全状态[29]，可认为故障不再继续扩散；

(2) 若A((Rk-1(i)p(E))＊p(V))⊂A((Rk-2(i)p(E))＊p(V))，则故障传播停止。这里不考虑故障累加的情况，即已经发生故障的节点不会发生二次故障。

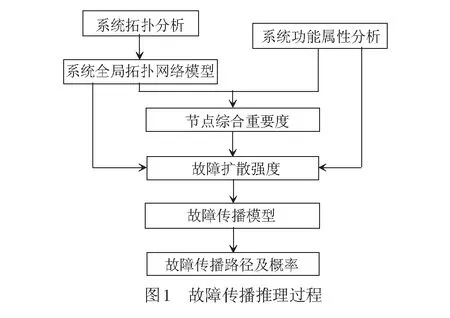
由系统故障传播模型式( 8 )，结合故障传播停止阈值可推理得到系统中任意部件故障后所有可能的故障路径以及该路径发生的概率，具体推理流程见图1。

4 动车组转向架系统故障传播分析

4.1 相关数据

为了验证所提出的基于改进多色集合的系统故障传播模型，以CRHX型动车组动车的转向架系统(这里将所有安装在转向架上的部件均视为转向架系统的一部分，如加速度传感器等)为例分析该模型的有效性。所需的实验验证数据来自某列车公司自2008年1月至2014年12月某CRHX型动车组故障处理的数据记录，其中转向架系统的故障记录共计1 918条，其数据记录见表2。

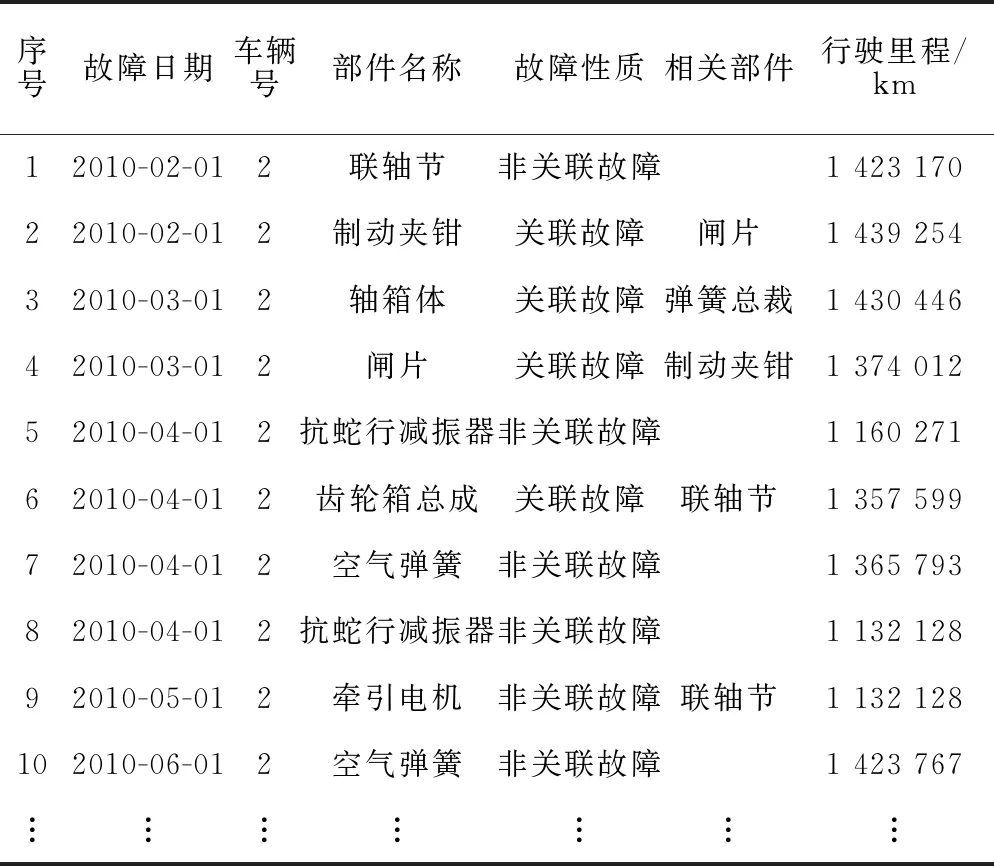
表2 转向架系统故障数据记录

首先在对动车的转向架结构充分调研的基础上，依据1.1节提出的方法构建图2所示的转向架系统全局拓扑网络，其中表3为模型中对应的部件明细。

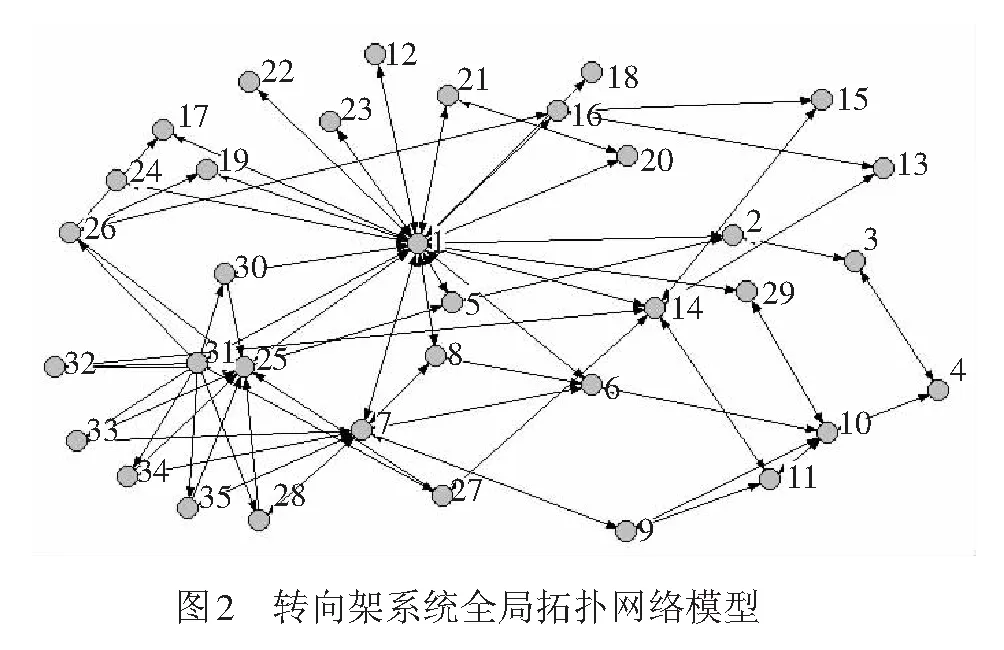
表3 转向架系统部件

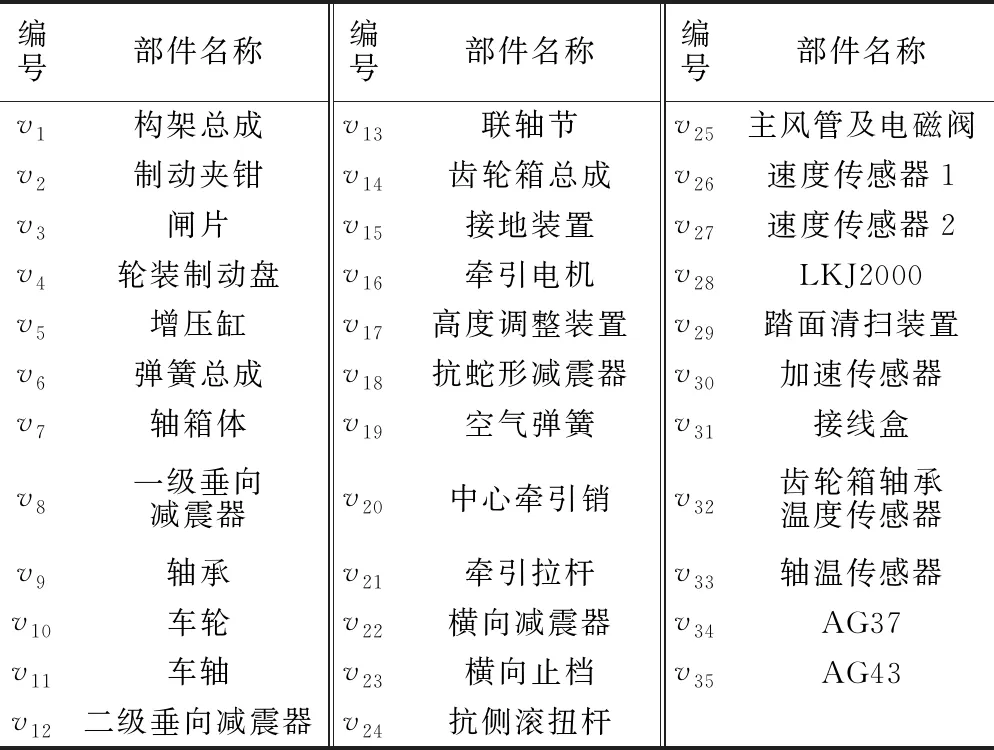
编号部件名称编号部件名称编号部件名称v1构架总成v13联轴节v25主风管及电磁阀v2制动夹钳v14齿轮箱总成v26速度传感器1v3闸片v15接地装置v27速度传感器2v4轮装制动盘v16牵引电机v28LKJ2000v5增压缸v17高度调整装置v29踏面清扫装置v6弹簧总成v18抗蛇形减震器v30加速传感器v7轴箱体v19空气弹簧v31接线盒v8一级垂向减震器v20中心牵引销v32齿轮箱轴承温度传感器v9轴承v21牵引拉杆v33轴温传感器v10车轮v22横向减震器v34AG37v11车轴v23横向止档v35AG43v12二级垂向减震器v24抗侧滚扭杆

结合转向架系统故障数据(见表3)以及关键部件的影响要素，得到转向架系统全局拓扑网络模型

G(V,E,f(V),f(E))

( 9 )

式中：Fv={μi,MTBFi}；Tv={bi,ci,di}；Fe={λij,pij,stij}

FM11FM12…FM1,35

FM35,1FM35,2…FM35,35

鉴于篇幅限制，这里不再详细的说明基于故障数据(见表3)和上述网络模型(见图2)的节点和边属性的计算过程及结果。

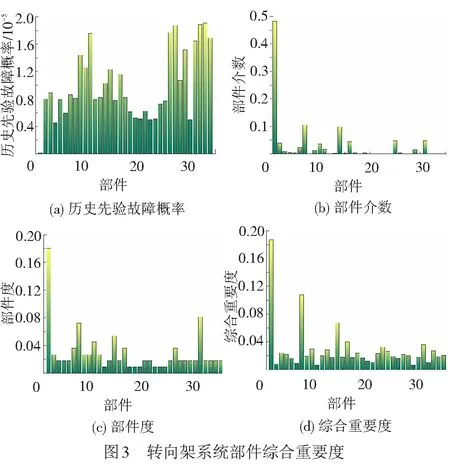
依据2.1节中综合重要度计算方法，利用Marichal熵理论和Shapley值[30]确定式( 3 )、式( 4 )中的权重μ，得到图3所示转向架系统中部件综合重要度排序为：构架总成>轴箱体>齿轮箱总成；由故障概率确定的部件重要性依次为：构架总成>轮装制动盘>接线盒；节点度的排序结果为：构架总成>接线盒>轴箱体；节点介数的分析结果为：构架总成>轴箱体>齿轮箱总成。可以看出4种测度在最关键部件的辨识结果是一致的，均为构架总成，但是其余部件的重要性有所差异；节点介数与综合重要度的前3个部件的辨识结果虽然相同，但从图3中可以明显看出综合重要度的辨识精度更高。历史先验故障概率、介数和度均为单一测度的关键部件识别，由于其关注侧重点不同且存在一定的随机性和不确定性导致辨识结果的差异性较大，而综合重要度则是从拓扑和功能重要性2个方面综合分析节点在系统中的重要程度，考虑的影响因素更全面，并且在一定程度上克服了单一测度辨识存在的不确定性影响。

4.2 转向架系统故障传播分析

系统故障传播模型式( 8 )中，ws、wp是节点故障传播影响因素的权重。若取权重ws=wp=0.5，则以FTI较高的节点v1、v7、v14和FTI较低的节点v2、v3、v16分别为故障源，依次计算转向架系统所有可能的故障传播路径及相应的路径发生概率(见图4、表4)。从表3中可以看出，节点v1发生故障后并未有传播路径发生，这是由于本文所提出的系统故障传播模型是以历史先验故障数据为基础的，作为转向架系统中最关键的骨架部件，构架总成几乎未发生过可能导致故障传播的故障模式，一旦其发生能够引发传播的严重故障对整个转向架系统的安全性影响是致命的，因此其在设计制造阶段的性能较高，在实际运行环境下的发生故障概率也较低。

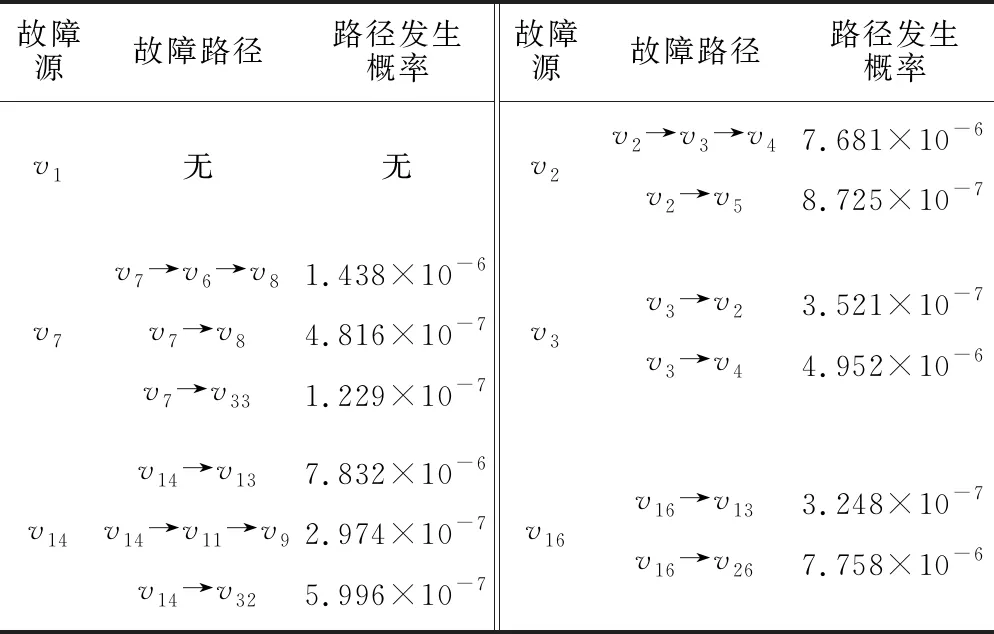
表4 故障传播推理结果信息(ws=wp=0.5)

图4给出了v7、v14、v2和v3故障后可能的传播路径图，不同颜色的线表示不同的传播路径。

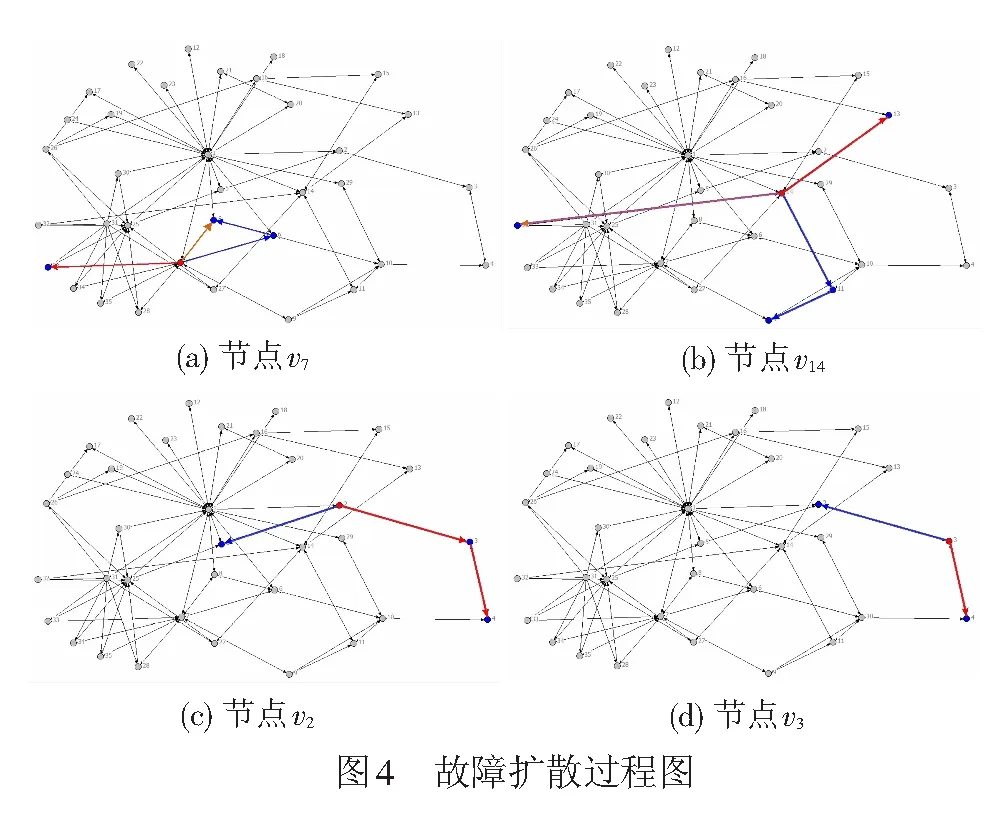
图5给出了参数ws(wp=1-ws)变化时各节点故障后最长的扩散步数。可以看出随着节点FTI在故障扩散强度中所占的权重增加，故障扩散的步数在降低，说明重要节点失效导致故障扩散深度降低，但对系统破坏程度增加，对系统安全性影响较大。这与本文之前所提出的关键节点失效将增加故障扩散强度是一致的。

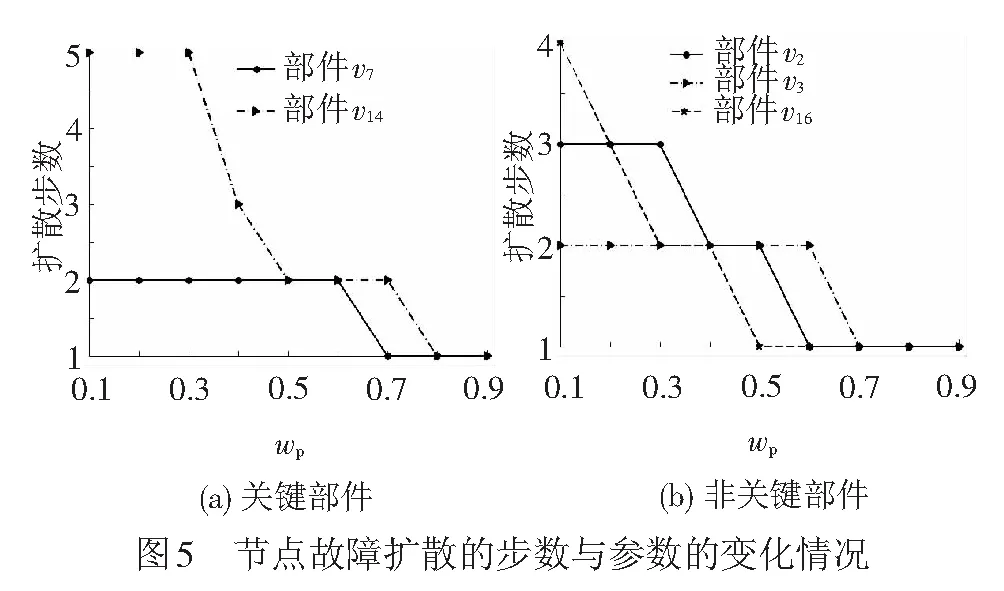
4.3 结果讨论

为了进一步说明本文所提出的系统故障传播模型的有效性，将与文献[2]、文献[28]所提出的方法以及由故障数据推理出的路径进行比较分析。文献[2]提出的利用蚁群算法求解的故障传播模型计算出转向架系统的高风险故障传播路径为v2→v3→v4→v10→v9。

从表5中可以看出，本文所提出的方法能够给出部件故障后多种可能的传播路径，而文献[28]仅能获得一条最有可能的传播路径，文献[2]也只能计算出整个系统中最高风险的单一路径。鉴于转向架系统故障传播影响因素的多样性，路径的选择和传播的深度也是不同的，仅给出单一传播路径对于系统安全性分析以及维修是不利的，而基于改进多色集合的系统故障传播模型可同时获得该部件故障所有可能的传播路径，有助于维修人员依据现场实际情况快速查找故障部件，降低经济损失。

表5同时也给出了由所记录的故障数据(见表2)推理得到的节点故障传播路径，可以看出故障数据推理得出的传播路径也具有多样性。通过对比发现，本文所提出的故障传播模型的计算结果与由故障数据推理得出的路径一致程度最高。

表5 故障传播结果比较

5 结论

本文在总结现有的故障传播建模分析方法及其优缺点的基础上，提出基于改进多色集合的系统故障传播模型，其主要包括：

(1) 以复杂网络理论为基础，结合系统功能属性建立了系统全局拓扑网络模型作为分析系统故障传播的基础。

(2) 综合考虑部件拓扑和功能双重属性，提出了基于Choquet积分的节点综合重要度计算方法。

(3) 以建立的全局拓扑网络模型为基础，提出了由节点综合重要度和故障模式所确定的节点扩散强度。

(4) 以节点扩散强度为基础，构建了基于改进多色集合的系统故障传播模型。以动车组转向架系统为例的研究结果表明，本文所提出的系统故障传播模型能够有效地分析系统中各节点故障后所有可能的故障传播路径以及相应各路径的发生概率。所构建的系统故障传播模型是以历史先验数据为研究基础，随着故障数据的积累，其分析结果也更加精确。另外，模型中并未考虑多因一果、共因失效等故障模式对系统故障传播的影响，在后续的研究中可考虑加入故障模式类型的影响。