钢中奥氏体晶粒长大规律
2019-08-16刘文月
刘文月 任 毅 王 爽 张 帅 高 红
(1.海洋装备用金属材料及其应用国家重点实验室,辽宁 鞍山 114009; 2.鞍钢集团钢铁研究院,辽宁 鞍山 114009)
Fe- C平衡相图中,温度超过727 ℃,在整个钢的成分范围内都可能存在奥氏体。向Fe- C二元合金中,添加不同种类的合金元素,可以改变奥氏体存在的温度区间与成分范围[1]。奥氏体晶粒长大规律符合Avrami法则,即晶粒尺寸是温度的幂指数函数,是时间的抛物线函数[2- 3]。
奥氏体晶粒的长大不是没有限制的,具有一个极限尺寸,Zener认为该尺寸由钉扎粒子的尺寸和数量决定[4- 6]。奥氏体晶粒长大过程中,会出现正常长大与异常长大两种现象。正常长大过程中,最大晶粒尺寸约为平均尺寸的2.5倍[7];异常长大过程中,仅有少数晶粒尺寸急剧增加,最大尺寸一般为平均尺寸的6倍以上,有时可达十几倍[8]。奥氏体晶粒的异常长大,也被称为二次再结晶[9]。
细化奥氏体晶粒,可以显著改善钢材的力学性能。在奥氏体单相区,对奥氏体施加一定量的塑性变形使之发生再结晶从而细化晶粒,是现代钢铁产品获得优异性能的常规工艺。无论是原奥氏体晶粒还是完成再结晶后的奥氏体晶粒,都具有相同的长大规律。了解奥氏体晶粒的长大规律,对控制钢材的最终性能具有重要意义。
现有预测晶粒尺寸的数学公式皆为经验公式,存在需要通过试验或模拟计算才能确定的未知常数,因此,需要进一步寻找更理想的模型来定量计算奥氏体晶粒尺寸。本文仅评述奥氏体正常长大过程中影响晶粒尺寸的因素、晶粒尺寸计算常用公式与晶粒尺寸确定方法等,尝试获得钢中奥氏体长大的定性与定量规律。
1 晶粒长大基本规律
奥氏体晶粒长大受Fe、C原子的扩散速率控制,其长大规律有如下定性认识[9]:1)晶粒长大是通过晶界移动而不是相邻晶粒合并的方式;2)晶界移动是不连续的,移动速率与方向都会发生改变;3)同一个晶粒的晶界可以向不同的方向移动,即部分晶界增加晶粒尺寸的同时,也允许另一部分晶界减小该晶粒的尺寸;4)晶界移动方向通常指向其曲率中心;5)二维晶界夹角的稳定数值为120°,非此角度晶界通过晶界弯曲与移动达到此稳定值;6)溶质原子与第二相粒子具有改变晶界移动速度的作用。
晶粒长大是分阶段的,不同阶段有不同的长大机制。Simpson等[10]在纯Pb、Cd及Pb基、Cd基低合金中,观察到了晶粒的四阶段生长模式。在奥氏体晶粒的等温生长过程中[11],晶粒生长一般都以具有最低激活能的方式首先生长;温度越低,激活能越小的生长机制持续时间越长;然后随着温度升高依次过渡到激活能更高的生长机制;高温时激活能低的生长机制很快完成而失去作用。高振英等[12]研究了中碳钢奥氏体晶粒的4种生长机制:1)Fe原子位错扩散控制机制;2)Fe原子位错、界面扩散控制的混合机制;3)界面扩散控制机制;4)Fe原子体扩散控制机制。
2 影响晶粒长大的因素
影响奥氏体晶粒长大的因素众多,主要有材料类型、温度、时间、长大机制、溶质原子数量与尺寸、钉扎粒子数量与尺寸及温度梯度等。晶粒的等温长大过程可以不考虑温度梯度的影响。而在非等温长大过程中,温度梯度对晶粒生长的影响较大。定量描述奥氏体晶粒长大规律,特别是区分各个影响因素对晶粒长大的作用,比较困难。1948年,Beck等首次给出了计算晶粒尺寸的经验公式[7,13]:
(1)
式中:D为平均晶粒尺寸,μm;k为与材料和温度有关的系数;t为保温时间,s;k0为材料常数;Q为激活能,J/mol;R为气体常数,8.314 J/(mol·K);T为绝对温度,K。
从Beck方程中可以看出,晶粒尺寸除了与材料有关,还与温度、时间和激活能有关。温度、时间对晶粒尺寸的影响满足Avrmi方程。激活能对晶粒尺寸的影响是一个综合性概念[14],它包含了溶质原子、钉扎粒子、长大机制、温度梯度等诸多因素的影响。
不同溶质原子对奥氏体晶粒长大的影响不同[1,8,15- 17],如表1所示。Moon等[2]、Lee等[16]的研究结果证实了Mo、Cr、Ni对奥氏体晶粒长大的抑制作用,提供了C、Mn抑制奥氏体晶粒长大的例证。

表1 溶质原子对奥氏体晶粒长大的作用[8,15]Table 1 Effect of solute atoms on austenite grain growth [8,15]
除溶质拖曳外,粒子钉扎是影响晶粒长大的最重要因素,可以用Zener方程[5,18]来描述:
(2)
(3)
式中:Rc为临界晶粒尺寸;r为粒子尺寸;f为粒子体积分数;K为Zener模型试验解析解系数;δ为指数常数;FZ为粒子钉扎力;KZ为Zener系数,γ为界面能。
由Zener方程可见,材料的临界晶粒尺寸Rc由材料中第二相粒子(包括夹杂物)的尺寸r和体积分数f决定[5]。因此,第二相粒子尺寸越小,数量越多,粒子钉扎力FZ越大,则材料的平均晶粒尺寸越小[19]。
Zener方程描述的粒子钉轧力,会随着温度、时间的变化因粒子尺寸与数量的变化而变化[1,19- 21]。随着温度的升高,粒子会发生析出、长大和溶解等一系列变化。钉扎粒子数量与尺寸的变化,导致在不同温度区间和时间段内的粒子钉扎力大小不同,这是Zener方程中系数K与指数δ取值多变(表2)的一个原因[1,5]。
粒子的溶解温度可以用固溶度积公式计算[26]:
(4)
式中:KS为平衡常数;X为微合金元素的质量分数,%;Y为碳或氮的质量分数,%;C1、C2为常数。

表2 不同指数δ取值时Zener模型试验解析解系数K的取值[1,5]Table 2 Analytical solutions of factor K in Zener model test with different exponential δ values[1,5]
*当钉扎粒子为TiN共格粒子时,K取值为2.10
由于试验和推导的基础条件不同,对于同一种粒子所得到的固溶度积公式也不同[22](见表3)。在Nb的质量分数为0.021%的合金中[23],因Nb/TiN之间的交互作用,不同温度下Nb固溶量的计算值是试验值的十几倍,甚至数十倍以上(见表4)。
除了公式本身的缺陷外,取样或制样不当也会给结果带来误差。1956年,Beck首先报道了晶粒长大过程中的“板厚效应”[7],即当晶粒长大到一定尺寸时,其长大速度会因试样尺寸过小而减小。若出现这种情况,会造成激活能的计算值严重偏大。 为了避免这种情况, 建议试样的最小截面尺寸至少为试验后平均晶粒尺寸的十倍。另外,为了消除观测误差,可通过冷加工的方式将样品表面去掉一部分,以消除试验过程对试样表面的影响,如脱碳、氧化等。如果样品尺寸允许,建议至少去掉2 mm。

表3 Nb溶解温度计算公式[22]Table 3 Formula for calculating Nb dissolution temperature[22]

表4 Nb的质量分数为0.021%的合金中Nb固溶量的计算值与试验值[23]Table 4 Calculated and experimental contents of solid solution Nb in alloys with 0.021% Nb by mass[23]
在奥氏体晶粒的非等温长大过程中,除了以上影响因素,还有其特有的影响因素。钢中奥氏体晶粒的非等温长大主要发生在铸造、热轧与焊接等过程中。与晶粒等温长大相比,非等温长大由于温度场的存在而具有不同的特征(见表5)[4]。

表5 非等温过程晶粒长大特征[4]Table 5 Characteristics of grain growth during non- isothermal processes[4]
3 常用的描述奥氏体晶粒长大的经验公式
为了描述方便,本文将与奥氏体晶粒长大相关的数学公式中所采用的符号做了统一。
Sellars等[24]引入了初始晶粒尺寸的影响,将Beck方程(式(1))做了等价改写(式(4)),改写后的形式已被广泛接受[1,5,7]。近年来,研究人员[25]联立Beck模型与Sellars模型,获得了第3种形式的Beck- Sellars模型(式(5))。
(5)
式中:Dt为t时刻平均晶粒尺寸;D0为起始时刻平均晶粒尺寸;n、n′为与材料、温度有关的指数;k为与材料、温度有关的系数;t为保温时间。
Beck、Sellars与Beck- Sellars 3种模型都存在与材料和温度有关的未知常量,为求得这些常量,需获得材料在不同温度和保温时间条件下的平均晶粒尺寸,然后对试验结果回归分析,求得这些未知常量的试验解,最终得出计算平均晶粒尺寸的经验公式。任何满足Avrami方程的晶粒长大模式,都可用这些模型来描述[1,13]。
在实际应用中,Beck、Sellars与Beck- Sellars 3种模型公式都需要做一定的变换才能使用。为了区分材料与试验温度的影响,将参数k、M改写为Arrhenius方程的形式(式(6)、式(7) )。对式(1)求导数,得到晶粒长大速度式(8);式(9)是晶粒长大速度的另一种表现形式,联立这两个方程,可得m与n之间的关系式(式10)。考虑Zener钉扎力的影响,可得式(11)。式(1)、式(5)、式(8) 和式(11)都是较为典型的晶粒尺寸表达形式,其典型取值如表6所示。
(6)
(7)
(8)
(9)
(10)
(11)
式中:k、M为与材料、温度有关的系数;k0、M0为与材料有关的系数;n、m为与材料、温度有关的指数;Q为激活能,J/mol;R为气体常数,8.314 J/(mol·K);T为绝对温度,K;D为平均晶粒尺寸;ν为晶界迁移速率;ΔF为晶界驱动力;γ为晶界表面能;r为粒子尺寸;f为粒子体积分数;KZ为Zener系数。
式(6)~式(11)没有考虑应变、应变速率对奥氏体晶粒尺寸的影响,因此,再结晶晶粒尺寸Ddrx的计算,通常使用Zener- Hollomon参数[18,26]来构造(式(12)、式(13)),它们分别是Sellars幂指数模型[18,24,27]与Sekine半对数模型,前者获得了广泛的试验支持。
Ddrx=cZ-nd
(12)
Ddrx=lgaZ-b
(13)
式中:Ddrx为再结晶平均晶粒尺寸;nd、a、b、c为常数;Z为Zener- Hollomon参数,s-1。
获得Ddrx首先要确定Z参数,Z参数的确定需测得材料在不同温度和应变速率下的应力- 应变曲线,然后对曲线进行拟合得到Z参数中未知的试验常数,再对Z参数与晶粒尺寸Ddrx进行拟合,确定Sellars幂指数模型与Sekine半对数模型中的未知试验常数,即可获得晶粒尺寸Ddrx与Z参数之间的函数关系。Sellars幂指数模型是用于计算动态再结晶晶粒尺寸的使用最广泛的经验公式,表6给出了模型中系数c与指数-nd的一些取值实例。
Z参数有3种形式[24],分别适用于不同的应力范围,式(14)适用于整个应力范围,式(15) 适用于低应力范围(ασ<0.8),式(16) 适用于高应力范围(ασ>1.2)。


表6 描述奥氏体晶粒长大的经验模型试验解Table 6 Experimental results on empirical models describing austenite grain growth
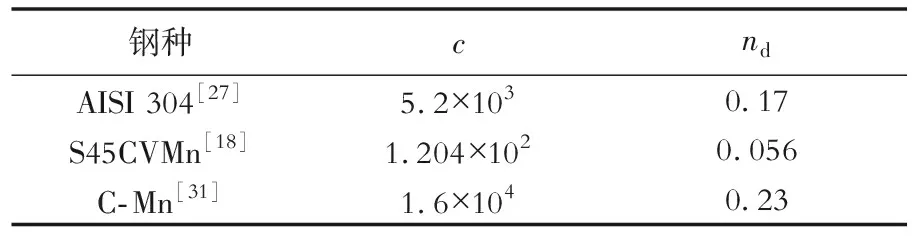
表7 Sellars幂指数模型中D- Z关系式试验解Table 7 Experimental relationship between D and Z in the Sellars power exponent model
获得Z参数的可计算形式后,可将材料的应变与峰值应力描述为式(20)、(21),通过热变形试验获得试验拟合解后,即可建立该材料高温变形的本构方程,用于描述材料在再结晶阶段的应力- 应变关系。结合式(12)、式(13)、式(20)与式(21)即可获得奥氏体再结晶晶粒尺寸。
(14)
Z=A1σq1
(15)
Z=A2exp(βσ)
(16)
(17)
(18)
β=α·q1
(19)
ε=A′Zq′
(20)
σp=A″Zq″
(21)

4 结语
奥氏体晶粒长大遵循扩散控制机制,其晶粒尺寸是温度的幂指数函数,是时间的抛物线函数。钢中奥氏体晶粒长大是分阶段的,不同阶段有不同的控制机制,表现为Fe、C原子扩散方式的改变。晶粒尺寸除了与溶质原子有关,还与温度、时间和激活能有关,另外第二相粒子对晶粒的长大速度也有一定影响。为了定量描述这些影响因素,建立了一系列的经验公式。公式中含有与温度和时间相关的试验常数,需要进行一系列的试验来确定。虽然理论计算或计算机模拟可以在一定程度上确定钢中奥氏体的晶粒尺寸,但是具有很大的局限性。而应用最广泛的经验公式具有不可预测的缺点。因此,开发出具有可预测的计算公式或者使用广泛的模拟计算方法,是今后奥氏体晶粒定量化研究的方向。
