基于概率假设密度滤波的水下多目标被动跟踪
2019-08-16李钢虎李亚安王春玮
王 芳,李钢虎,李亚安,张 雪,王春玮
(西北工业大学 航海学院,陕西 西安 710072)
0 引 言
概率假设密度(PHD)滤波是一种基于随机有限集理论的多目标贝叶斯滤波,对多目标跟踪过程中的目标随机出现、分裂、消失、漏检和虚警杂波等现象有着严格的数学描述,它代表着多目标跟踪技术的一个新方向[1]。通常,实现递推传递概率假设密度函数的多目标跟踪算法比较困难,Vo 等利用粒子滤波技术给出了PHD 滤波器的近似实现形式[2],简称为PFPHD 滤波算法,这就加快了PHD 滤波的工程应用。
文献[3]中将势分布概率假设密度滤波(CPHD)应用于水下多目标跟踪,并针对传感器量测的不确定性,在CPHD 滤波的框架下引入量测的幅值信息,增加数据关联的可靠性。文献[4]探究了基于多波束前视声呐数据的2 种不同多目标跟踪方法,一种方法是给每个目标分配卡尔曼滤波器,通过设定量测门限和数据关联技术进行目标跟踪,另一种是应用PF-PHD 滤波算法结合数据关联技术的目标状态估计。仿真表明PHD 滤波器比传统卡尔曼滤波方法更优越。文献[5]利用声信号得到目标的距离测量信息,采用蒙特卡罗方法实现的PHD 滤波器成功地跟踪3 个水下自主航行器(AUV)。文献[6]通过单一的水下传感器获得目标位置量测信息,针对杂波存在时,通常的跟踪算法仅依赖当前的位置观测,故使用高斯混合概率假设密度(PHD)前向-后向平滑算法,它是利用多个量测数据对滤波值进行平滑,进而减小目标估计的位置误差。结果表明在高密度杂波的水下环境中该算法表现良好。
目前大部分文献侧重研究目标的主动跟踪,实际上,被动跟踪在某些方面更具应用价值。本文采用PFPHD 滤波算法对监测区域内目标进行跟踪,并利用双被动声呐[7]来获得目标的方位角信息。
1 双被动声呐系统观测模型
假设二维监测区域内有多个目标,采用匀速运动(CV)模型模拟每个目标的位置变化情况。采样时间为 T , 其中一个目标 k时刻的状态矢量表示为包括目标分别在 x,y方向上位置和速度。那么,任意目标的状态方程可表示为:

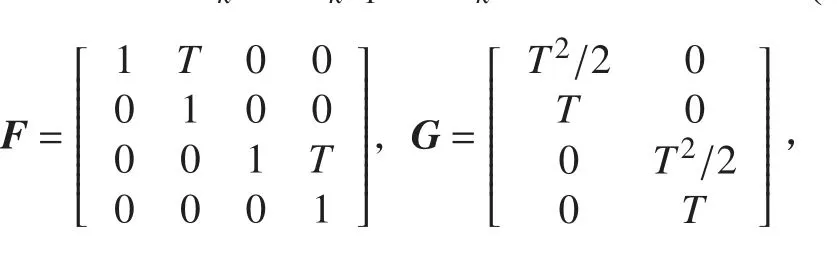
其中,
假设观测平台上装备有仅得到目标角度观测信息的2 部被动声呐基阵,等效于雷达跟踪中的2 个测向传感器,那么这里传感器个数为2,接下来文中描述的单个传感器均指单被动声呐基阵,并且假设被跟踪目标与声呐设备在一个平面上,以便研究算法特性。令为第 s 个传感器的位置。则对于第 s个被动传感器,可以得到目标的方位角:
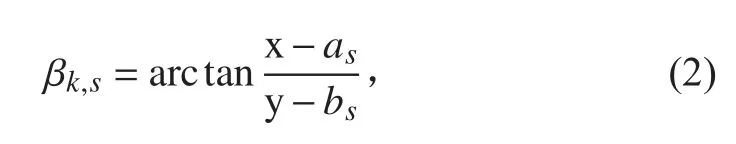
则对于第 s个传感器量测方程:
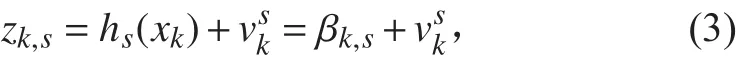
2 概率假设密度(PHD)滤波
2.1 随机集(RFS)的多目标模型
多目标跟踪中当每一时刻目标数、杂波或虚警个数不同时,状态空间和量测空间的维数也会随之变化,此时目标跟踪的模型应表示为各个目标状态和量测的集合。基于随机集理论的跟踪模型有着坚实的数学基础,能准确地描述多目标跟踪中目标产生、消失、衍生等现象。


2.2 PHD 滤波原理
针对多目标跟踪中Bayes 公式难求解的问题,Mahler 提出了概率假设密度(PHD)滤波近似实现多目标Bayes 滤波器,PHD 滤波通过递推多目标后验密度的一阶统计矩来降低计算复杂度。
滤波预测方程:
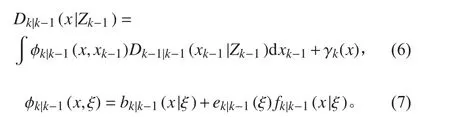
PHD 滤波更新方程:

对式(8)中的P H D 函数 的积分,即为,然后对取整得到目标数的估计值。进一步由 的个峰值点所在位置,得到 时刻个目标的状态向量。
2.3 多目标跟踪的PF-PHD 滤波
PF-PHD 滤波是利用一系列离散的带权重的样本近似相应的PHD 函数,通过聚类算法提取目标的状态估计,当粒子数目达到一定程度,PF-PHD 滤波逼近Bayes 最优估计,文献[2] 详细介绍了粒子滤波实现PHD 滤波的原理及具体步骤。
传统的PHD 滤波器的应用前提是单传感器,对于多传感器的情况,也有相应的算法提出,比如一种利用所有传感器的量测更新PHD 的迭代更新近似算法[8],以及Mahler 提出的一种乘积形式的多传感器PHD 滤波算法[9],这些算法的共同缺点是计算复杂度大。本文根据文献[10],采用集中式融合策略,在第k 时刻,将各个传感器的观测统一送至数据融合中心,假定量测数据已完成配准及关联,这样就可以将多传感器问题转化为单传感器问题,进一步简化多目标跟踪算法。
3 仿真实验
考虑二维监测区域范围为[-3000 m,3000 m] ×[-3000 m,3000 m],进入监测区域的目标都作匀速直线运动且航速约40 kn,即,利用双传感器进行纯方位角跟踪。仿真中采样间隔 T =5s,总步长为60,目标检测概率, 目标存活概率 e=0.99,杂波数服从泊松分布且杂波在跟踪场景内在 [-π,π]上服从均匀分布,新生目标强度函数的高斯分量权值均为0.1,不考虑目标的衍生。采用OSPA 距离作为多目标跟踪的评价指标,侧重评价目标跟踪的距离误差,因此OSPA 距离参数设为:。初始粒子数为500,每个实验均进行50 次Monte Carlo 仿真。
1)实验1 单目标跟踪
假设监测区域内只有一个目标,沿横坐标 x 方向航行,航速为40 kn。为研究目标和两传感器连线初始链距(简称目标初始链距)、双站距离对算法跟踪性能的影响,将目标初始链距记为,两传感器间距记为S ,单位为 m ,令 S,D=500:500:6 000,即初始距离为 500 m 且以5 00 m的步长变化。
仿真中单个目标在 k=1 时刻出现, k=60时刻消失,位置单位为 m,速度单位为 m/s,假设目标初始状态为=[-3 000,20,(D-3 000),0]T,两传感器位置坐 标 分 别 为 (-3 000,-3 000), (S-3 000,-3 000)。目 标状态噪声方差矩阵 Q=diag[0.01,0.01],测量角度方差,不考虑杂波的干扰。新生目标强度函 数 为 γk(x|r)=0.1×, 协 方 差 矩 阵=diag[100,4,100,4]。
二维搜索得到的结果是当两传感器间距和目标初始链距以 500 m 步长同时从 500 m 变化到 6 000 m时,单目标位置估计的均方根误差变化情况。从得到数据初步判断,在某一传感器间距大小一定时,随目标初始链距增大,则目标估计的均方根误差总体呈上升趋势,算法的估计性能下降;同理,固定某一初始链距大小,目标估计的均方根误差随着传感器间距增大而总体呈下降趋势。这一直观结果与文献[7]吻合。假设单目标位置估计的均方根误差在 10 m内是可以接受的,那么,当且 S时,算法的性能更优越,这就表明二维搜索能够有效确定参数的最佳取值范围。
进一步分析数据标准差,判断目标估计均方根误差对参数变化的敏感程度。固定每一个传感器间距S 的值,对变量目标初始链距 D求其标准差,同样固定每一个目标初始链距 D 的值,计算变量传感器间距 S的标准差,数据标准差变化显示在图1。根据图1,当传感器间距变化时,目标初始链距对应的均方根误差的标准差一直在1 0 m以上,而且不断增大,相比之下,当目标初始链距变化,传感器间距对应的均方误差的标准差有超过 80%的 值在1 0 m以下。这就表明目标估计的均方根误差对于目标初始链距的改变更敏感,因此,利用2 个传感器进行目标跟踪时,可以首先确定出合适的传感器间距。
图2 表示目标估计均方根误差均值随传感器间距变化情况,其中均值指的是各初始链距对应均方根误差的均值。将实验2 和实验3 的传感器间距设置为3 000 m,此时图2 中曲线趋向平稳。
2)实验2 多目标编队航行的场景
假设目标编队航行,各目标的间距为 DIS ,单位为 m,目标速度设为40 kn,沿横坐标 x 方向航行,为保证在正确估计目标数情况下研究目标间距对算法的影响,故将目标数目设置成随时间变化。
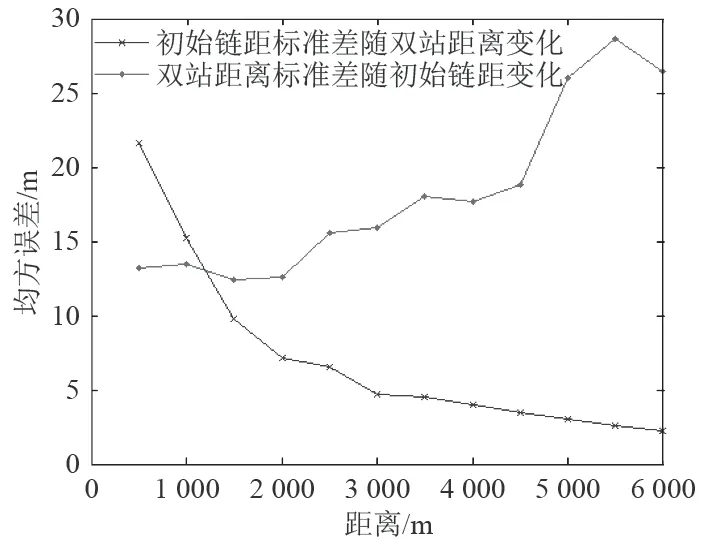
图 1 数据标准差变化Fig. 1 Standard deviation of data

图 2 均方根误差均值变化Fig. 2 Mean value of root mean square error
假设监测区域内存在3 个目标,位置单位为 ,速度单位为 。目标1 初始状态为 ,目标2 初始状态为 ;目标3 初始状态为 ,取各目标间距,分别进行实验仿真。其中各目标出现和消失的时刻与实验一相同。2 个传感器位置分别为 , 。状态噪声方差矩阵 ,测量角度方差为。杂波数服从 的泊松分布,则虚警PHD 为 。新生目标强度函数为:,协方差矩阵与实验1 相同。
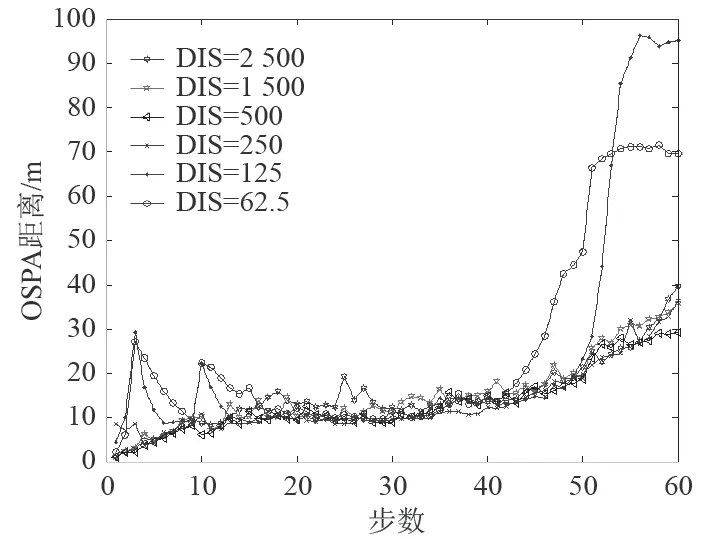
图 3 不同 DIS取值下的OSPA 距离Fig. 3 OSPA distance under different DIS values
3)实验3 航迹交叉的场景
假设监测区域内存在3 个目标,位置单位为 m,速度单位为m /s。 目标1初始状态=[-2500,18,1000,0]T,目标2 初始状态=[2 000,-15,2 000,-12]T,目标3 初始状态为=[-2 000,18,2 000,-14]T,其中各目标出现和消失的时刻与实验1 相同。两传感器位置、虚警PHD 和新生目标强度函数与实验2 相同。考虑实际情况,假设目标状态噪声方差矩阵Q =diag[0.04,0.04],测量角度误差从1°变化到3°。
由图4~图6 知,当目标航迹发生交叉时,量测角度误差保持在2°以下时,采用PF-PHD 算法能够对监测区域内每时刻存在的目标进行跟踪,且目标跟踪精度很高。对于角度量测误差超过一定范围时,在航迹交叉点和交叉区域内目标跟踪偏离程度高,效果很差,因此算法对于声呐基阵的测向精度有一定要求。
4 结 语

图 4 目标位置估计Fig. 4 Target position estimate
本文研究了基于概率假设密度滤波的水下多目标m m/s x1,1=[-3000,20,0,0]TTDIS =2 500,1500,500,250,125,62.5(-3 000,-3000) (0,-3 000)Q=diag[0.01,0.01]σ2v=(1×π/180)2r=5κk(y)=r/(2π)2+跟踪技术,针对算法中两声呐距离和目标初始链距2 个重要参数取值的问题,提出的二维搜索法能够有效指导实际目标跟踪中算法的参数选取,并且通过数据分析得出单目标跟踪的精度对于目标初始链距的变化比两声呐间距变化更敏感这一重要结论。同时,对于多目标编队航行和航迹交叉情况,仿真结果表明算法的高效性和稳定性。
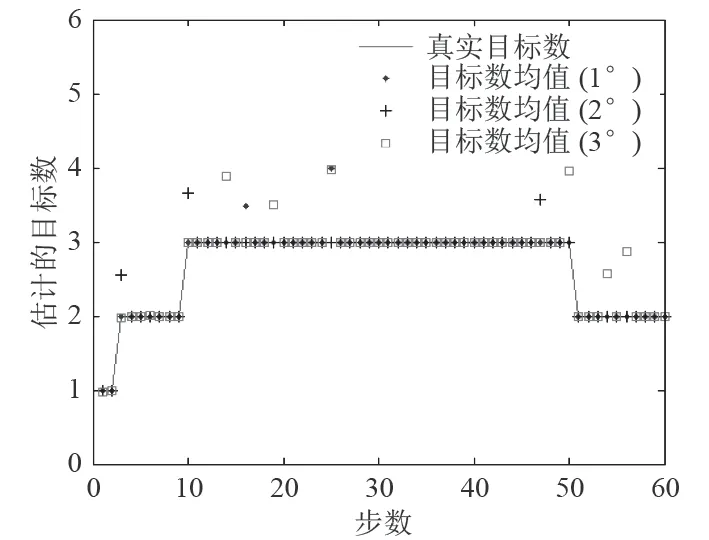
图 5 目标数估计Fig. 5 Target number estimate

图 6 OSPA 距离Fig. 6 OSPA distance
