基于ADS的传输线时域分析实验

潘玉剑，罗国清

(杭州电子科技大学 电子信息学院，杭州 310018)

0 引 言

学生在学习微波技术基础或微波电路等微波相关课程之前，已经学过电路分析以及模拟电路等低频电路课程。但与这些低频电路课程不同的是，微波相关课程第一次提出了传输线的概念，以及与之相关的反射以及传输线阻抗匹配。从课堂学习状况来看，学生对反射以及传输线阻抗匹配概念的理解大都停留在数学公式的层面，并且产生了不少疑问，比如“低频是否也有反射”“为什么低频电路不考虑传输线阻抗匹配”等。

虽然这些问题可以从数学公式层面予以解答，但单纯公式难以让学生领悟到其物理内涵。为了让学生对反射及传输线阻抗匹配有深入的理解，可以考虑搭建物理实验平台，利用仪器来进行实验教学。但在微波频段，仪器大都比较昂贵，且演示波的反射的操作较繁琐，教学成本较大。对此有不少学者提出利用相关软件仿真进行虚拟实验教学[1-4]。对于传输线的实验教学，文献[5]中提出了利用先进设计系统 (Advanced Design System,ADS)软件来演示传输线各种条件下的电压、电流分布及阻抗变化。但该实验实质是对数学公式的可视化操作，并未涉及时域分析，无法反映物理本质。为了触及传输线反射及匹配的物理本质，需要进行时域分析，观察电路同一位置不同时间点的电压波形的变化。对于电路的时域分析，除了有ADS软件可以利用，还有PSpice[6-7]，Multisim[8-9]等软件。但是ADS主要是一款微波仿真软件[10-13]，偏向于微波信号的仿真，对于微波类相关课程是较优的选择。对于时域仿真，可以利用ADS软件自带的瞬态仿真 (Transient Simulation)组件来完成。

本文基于ADS软件设计了传输线时域分析的教学实验。首先，利用传输线时域多次反射的观点，理论上推导出通用传输线模型不同时间点的电压波形，为实验奠定理论基础；其次，基于ADS设计出传输线终端短路和开路的实验，使学生可以直接观察电压及其反射的时域波形；最后，基于ADS设计出传输线阻抗匹配实验，让学生能够从时域感受并理解传输线匹配的重要性。该实验教学能让学生学习到传输线反射及匹配的物理本质。

1 理论分析

理论分析之前需要建立相关模型。首先，我们定义一个通用传输线模型，如图1所示。

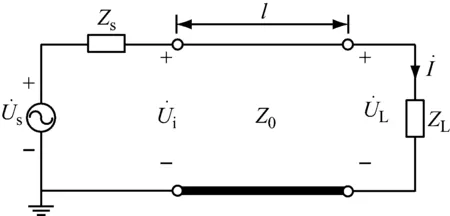
图1 通用传输线模型

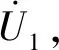
(1)

假设信号由传输线到负载以及由传输线返回到源阻抗的反射系数分别为ρL与ρS，根据传输线反射系数知识可知:

(2)

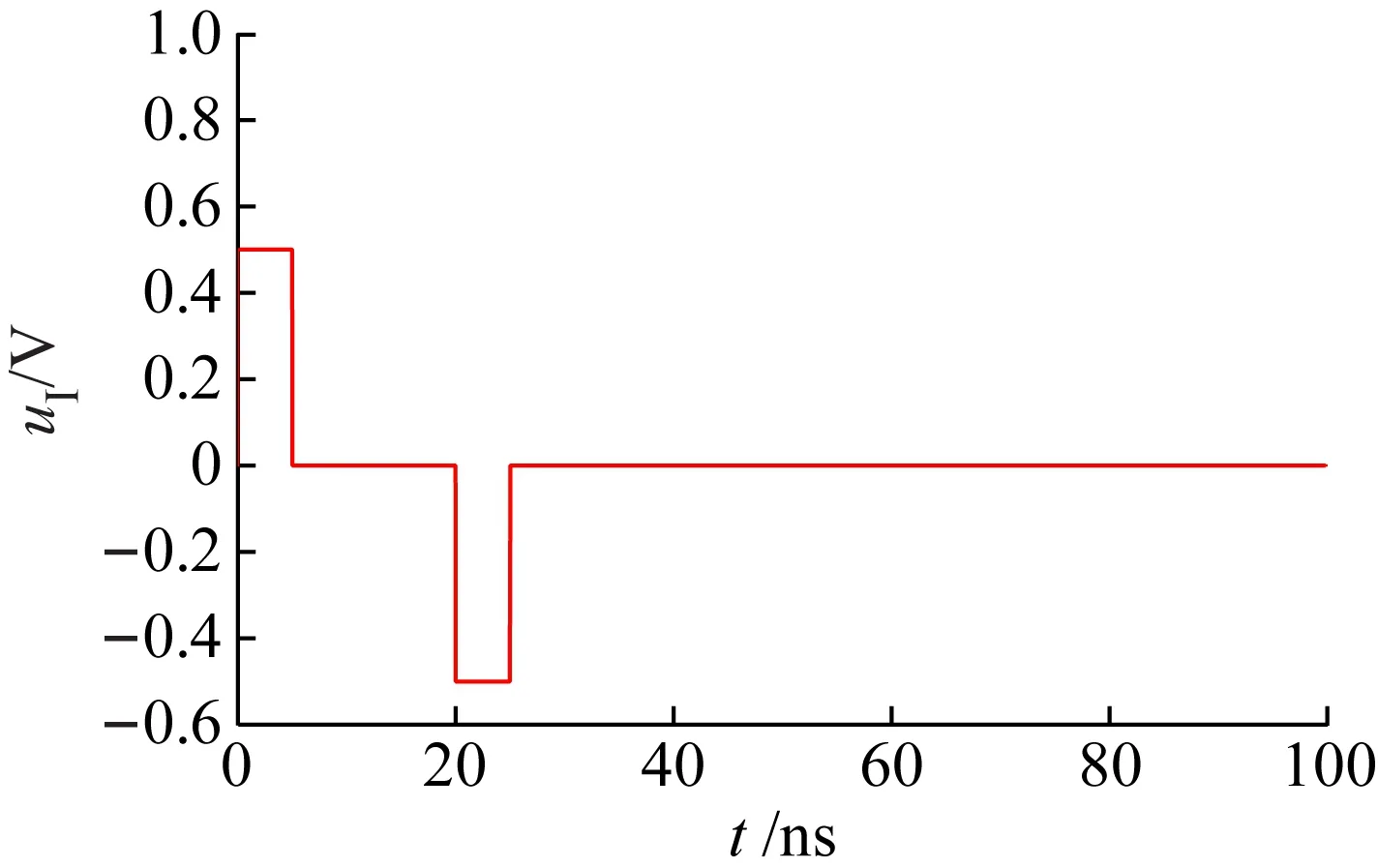
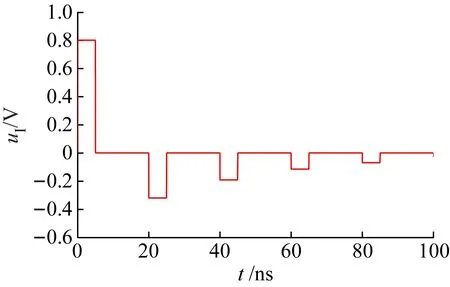
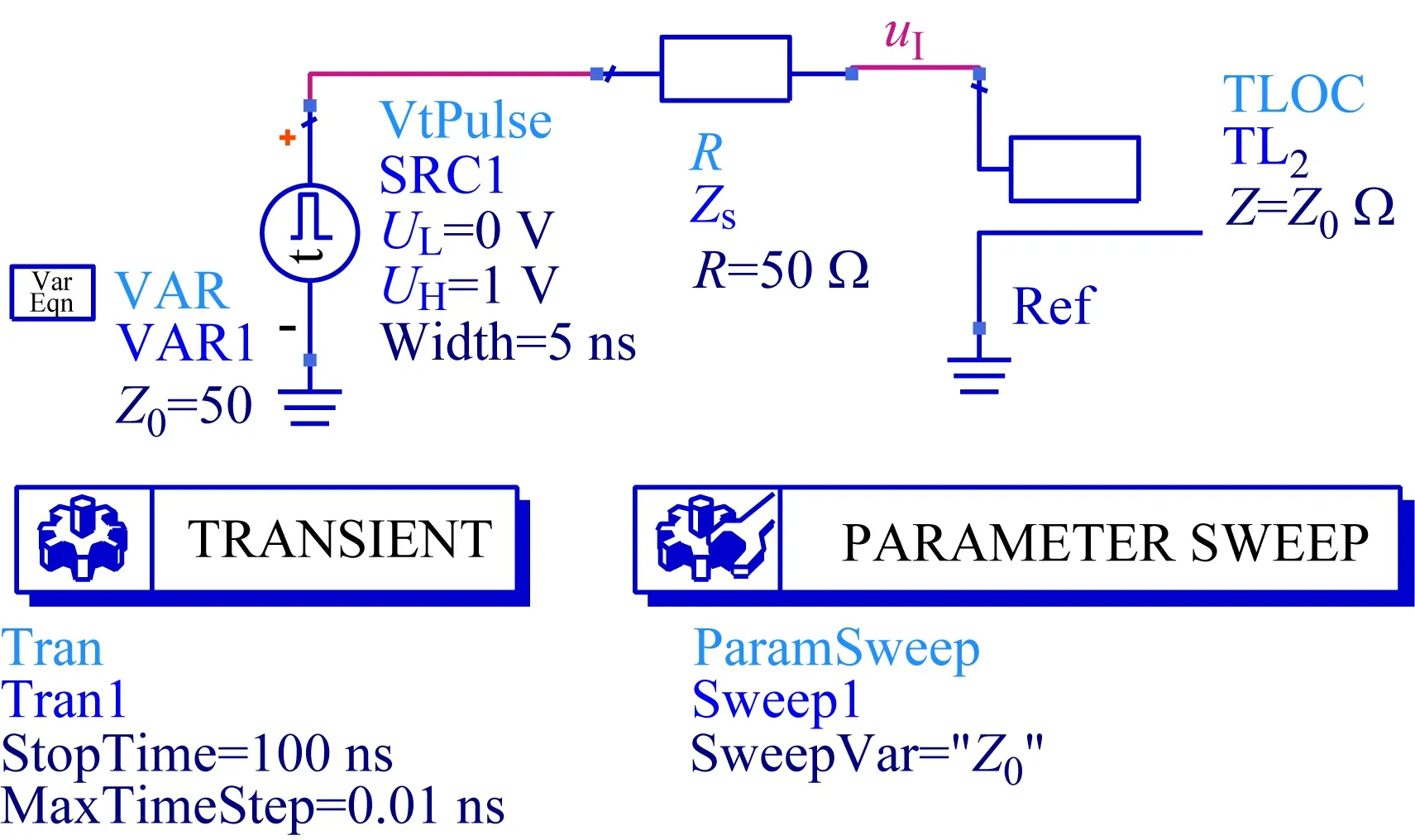
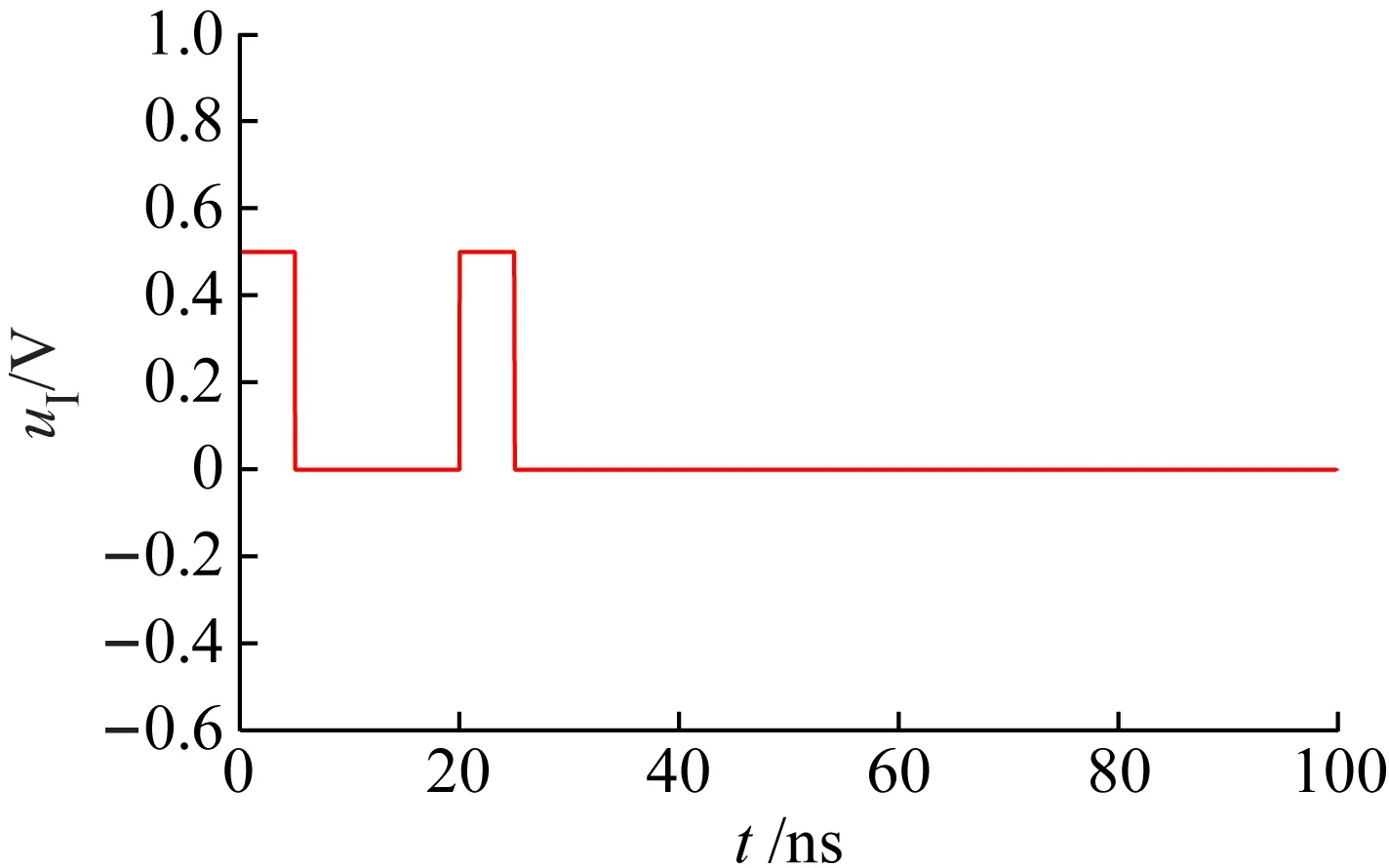
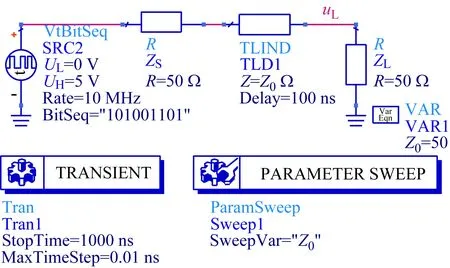
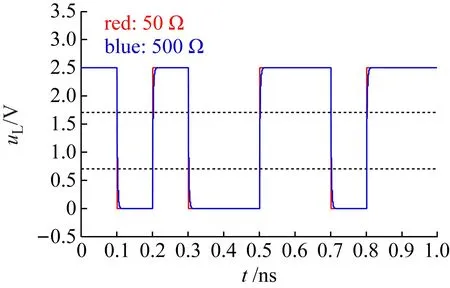
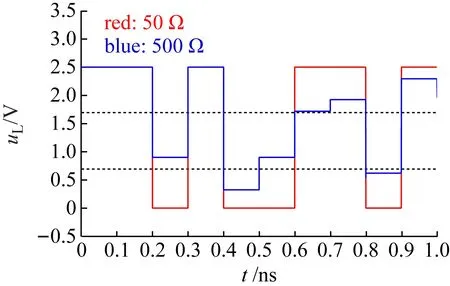
再假设电压信号刚达到传输线输入端的时刻为t=0，传输线信号时延为T，则当0≤t

(3)

当T≤t<3T时，信号经过一次负载反射后与原信号进行了叠加，所以有

(4)

式中：γ=α+jβ；α为衰减因子；β为相位常数。当3T≤t<5T时，前述信号，即式(4)的信号，经过了一次负载反射和一次源反射后与自身进行了叠加，得到

(5)

当5T≤t<7T时，前述信号，即式(5)的信号，经过了一次负载反射和一次源反射后与式(4)进行了叠加，得到

(6)

以此类推，当(2n+1)T≤t<(2n+3)T时，可以得到

(7)

式中，n可理解为信号从传输线到源端并反射的次数。

(8)

上式正是低频电路中的电压分配公式，最终的负载电压与传输线特性阻抗Z0无关。以上是用时域多次反射的观点解释了“为何低频电路不用考虑传输线阻抗匹配”。但需要注意的是这里的低频是相对于传输线长度l大小来衡量的，当传输线长度l很大时，低频信号就不是缓变的，从而等效成高频信号，此时就需要考虑传输线阻抗匹配。以上分析结果同样可从传输线输入阻抗公式得出，传输线输入端的阻抗可写为[14-15]

(9)

当l很小时，传输线输入阻抗可近似为ZI≈ZL，而与传输线特性无关，即不用考虑传输线阻抗匹配。但是单纯式(9)难以让学生领悟其物理内涵。

2 ADS建模仿真实验

在学生从时域多次反射角度在理论层面理解了传输线反射与传输线阻抗匹配后，可以设置基于ADS的时域仿真实验，让其从实验层面直观感受并加深理解。对于时域仿真，采用ADS的瞬态仿真组件，并设计了3个实验，分别是传输线终端短路时域分析实验、传输线终端开路时域分析实验以及传输线阻抗匹配时域分析实验。需要注意的是，为了简化实验教学，仿真中采用的传输线皆为无耗传输线。

2.1 传输线终端短路时域分析

在ADS中建立如图2所示的原理图。其中SRC1为时域脉冲源，脉冲幅度设置为1 V，脉冲宽度设置为5 ns。ZS为源阻抗，设为50 Ω。TL1为终端短路传输线，其特性阻抗Z0分别设置为50 Ω与200 Ω，传输线时延T设置为10 ns。图中放置了瞬态仿真器(TRANSIENT)，并利用参数扫描器(PARAMETER SWEEP)实现对50 Ω与200 Ω的特性阻抗进行同时仿真。图中uI为传输线输入端口的电压，是仿真时需要观察对象。

图2 传输线终端短路时域分析原理图

仿真结果如图3所示。图3(a)为特性阻抗为50 Ω的传输线输入端的电压时域波形。第1个脉冲为第1次进入传输线的波形，其幅度为0.5 V，符合式(1)的结果。第2个脉冲为经过终端短路点反射的电压，与第1个脉冲间隔时间2T=20 ns，由于短路对应的反射系数ρL=-1，所以波形出现了电压翻转，变为-0.5。最终由于源阻抗与传输线阻抗匹配，返回源阻抗的波不再被反射。图3(b)为特性阻抗为200 Ω传输线输入端的电压时域波形。由于传输线阻抗为200，所以第1个脉冲的电压变为1×200/(200+50)=0.8 V。第2个脉冲为第1个脉冲经过一个短路点反射与其经过一个短路点反射再一个源阻抗反射后叠加的波形，电压为(1+ρS)×ρL×0.8=-1.32 V。此后经源阻抗反射的脉冲继续向终端传播并继续在两端之间反射，周而复始。在这过程中幅度逐渐减小直至为0 V，进而停止反射。

(a)50 Ω特性阻抗

(b)200 Ω特性阻抗

2.2 传输线终端开路时域分析

在ADS中建立如图4所示的原理图，与图2不同的是，终端短路TL1变为终端开路结构TL2。其余参数与图2相同。

仿真结果如图5所示。图5(a)为特性阻抗为50 Ω的传输线输入端的电压时域波形。与短路情形不同的是，第2个脉冲的幅度为0.5 V，这是由于开路时的终端反射系数ρL=1。由于源阻抗与传输线匹配，第2个脉冲后不再有发射波。图5(b)中，由于源阻抗为200 Ω，与传输线不匹配，故第2个脉冲后还继续出现反射波，其分析与图3(b)类似，此处不再重复。

图4 传输线终端开路时域分析原理图

2.3 传输线阻抗匹配时域分析

在ADS中建立如图6所示的原理图。这里SRC2表示一个二进制信号源，“1”用高电平5 V表示，“0”用低电平0 V表示。源阻抗ZS为50 Ω，TLD1为理想传输线，终端负载阻抗ZL为50 Ω。实验中分别改变二进制码bit、码率Rt、传输线特性阻抗Z0以及时延T，观察图中负载电压uL对应的二进制码传输正确性。

(a)50 Ω特性阻抗

(b)200 Ω特性阻抗

图6 传输线阻抗时域分析原理图

仿真结果如图7所示。图7(a)对应二进制“101001101”，码率10 Mb/s，时延1 ns的仿真结果。其中红色曲线表示传输线特性阻抗为50 Ω，蓝色为500 Ω。假定负载端以2.5 V LVCMOS电平标准来判定二进制数值[16]，两条虚线分别对应高低电平门限。可以发现，在此条件下，传输线匹配与否对波形影响很轻微，二进制不会发生误码。该结果说明一般情况下，低频信号不需考虑传输线阻抗匹配。

图7(b)在图7(a)的基础上增加了传输线时延，由1 ns改为100 ns，此时传输线长度为30 m。在如此长的延时上，即使是低频，发现不匹配相对于匹配对二进制码正确性影响很大。根据2.5 V LVCMOS电平标准，500 Ω传输线接收到的二进制码为“1Z10Z1101”，其中“Z”表示不符合电平标准而定义为高阻态，即有2 bit的二进制码传输错误。如果考虑噪声影响，误码率将会更高。此处的误码主要由传输线不匹配导致的反射造成，这也说明了低频是存在反射的。

图7(c)在图7(a)的基础上改变码率为1 000 Mb/s，改变二进制码为“011100101”，而其余条件不变。在如此高的频率上，即使时延很短，我们发现不匹配相对于匹配对二进制码正确性影响同样很大。根据2.5 V LVCMOS电平标准，500 Ω传输线接收到的二进制码为“0ZZ10Z101”，即有3 bit的二进制传输错误。如果考虑噪声影响，误码率同样将会更高。

(a)Bits:101001101,Rt=10 Mb/s,T=1 ns

(b)Bits:101001101,Rt=10 Mb/s,T=100 ns

(c)Bits:011100101,Rt=1 000 Mb/s,T=1 ns

实验表明，在低频短时延条件下，不需考虑传输线阻抗匹配。但在低频长时延或者高频条件下，必须要考虑传输线阻抗匹配。是否需要考虑传输线阻抗匹配的核心在于信号在所考虑的时延跨度上相位变化是否足够小或者是否属于缓变信号。

3 结 语

本文基于ADS软件设计了传输线时域分析的实验教学方法。首先，利用传输线时域多次反射的观点，理论上推导出通用传输线模型在不同时间点的输出电压波形，为实验奠定理论基础；其次，基于ADS设计出传输线终端短路和开路的实验，使学生可以直接观察电压及其反射的时域波形；最后，基于ADS设计出传输线阻抗匹配实验，让学生能够从时域感受并理解传输线匹配的重要性。该实验教学提供了一种让学生能够掌握传输线反射现象与传输线阻抗匹配知识的物理本质的实验教学方法。