指数运算中常用的方法与技巧
2019-08-14杜红全
杜红全
(甘肃省康县教育局教研室 746500)
在指数运算中,若能根据题目的结构特征选择适当的方法,则可以简化运算.下面举例说明.
一、利用整体代换
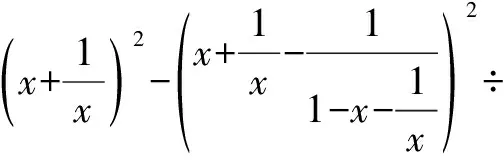
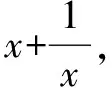
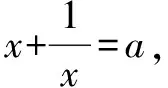
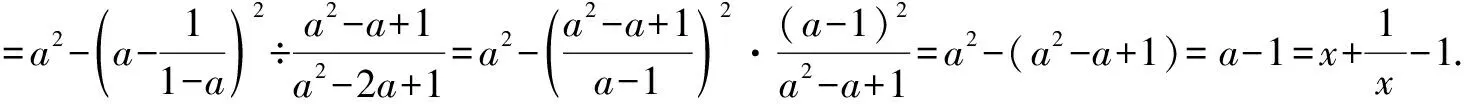
二、把小数化为分数、把带分数化为假分数
若底数(或指数)是小数时,则可化为分数;若底数是带分数时,则可化为假分数.
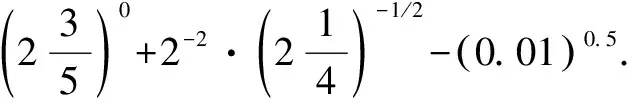
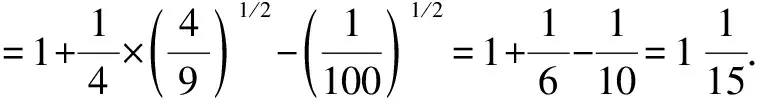
三、利用或
在指数运算中,把指数式进行因式分解或约分,可以使运算简化.
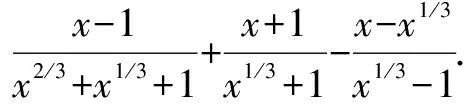
分析根据本题特点,应注意到
x-1=(x1/3)3-13=(x1/3-1)(x2/3+x1/3+1),
x+1=(x1/3)3+13=(x1/3+1)(x2/3-x1/3+1),
x-x1/3=x1/3[(x1/3)2-1]=x1/3(x1/3+1)(x1/3-1).
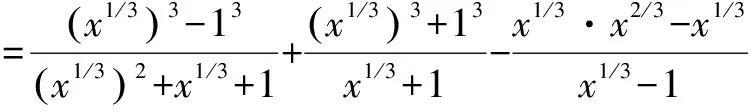
=x1/3-1+x2/3-x1/3+1-x2/3-x1/3=-x1/3.
评注解此类问题,还要注意运用指数运算中的乘法公式:
(a1/2+b1/2)(a1/2-b1/2)=a-b;(a1/2±b1/2)2=a±2a1/2b1/2+b;
(a1/3±b1/3)(a2/3∓a1/3b1/3+b2/3)=a±b.
四、利用根式与分数指数幂的互化
若底数是根式时,一般将根式统一写成分数指数幂的形式,然后进行运算化简;有时也可根据式子的结构特点把分数指数幂化为根式较为方便.
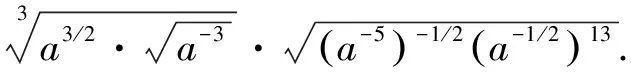
解原式=(a3/2·a3/2)1/3·[(a-5)-1/2·(a-1/2)13]1/2=(a0)1/3·(a5/2·a-13/2)1/2=(a-4)1/2=a-2.
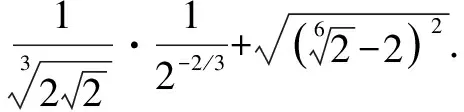
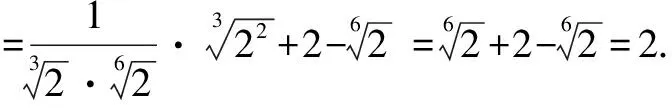
五、利用ap·a-p=1(a≠0,p是正整数)
在指数运算中,若灵活运用ap·a-p=1进行代换,则可以化难为易.
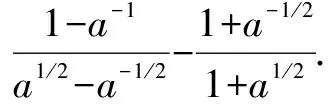
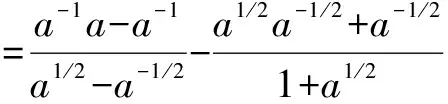
=a-1/2-a-1/2=0.
六、利用乘法公式
学习了负整数指数幂和分数指数幂以后,应习惯对负整数指数幂和分数指数幂直接应用乘法公式来计算,例如a-2-b-2=(a-1-b-1)(a-1+b-1),a2-2+a-2=(a-a-1)2,a-b=(a1/2+b1/2)(a1/2-b1/2)等.
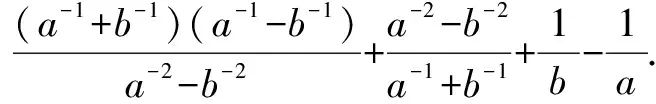
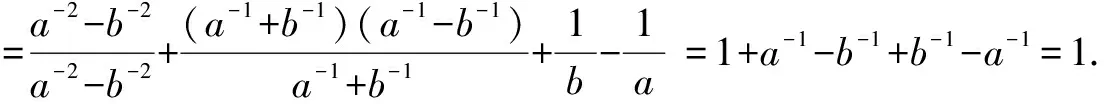
七、利用
利用这个性质,颠倒底数的分子分母的位置,直接把负指数化为正指数,反之亦然.
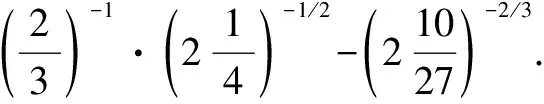
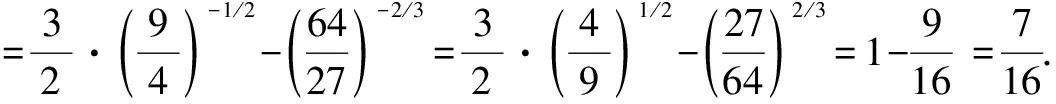
八、利用换元法
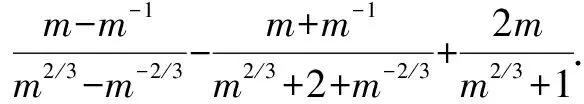
解设m1/3=x,m-1/3=y,则xy=1.