天车升沉补偿装置摆臂长度优化设计

张彩莹，郑万里，牟新明,李 欢，罗 强

(宝鸡石油机械有限责任公司 研究院成都分院，成都 610000)

海洋钻探作业中，由于外界风、浪的作用，会导致钻井船/平台发生周期性的摇摆、平移等运动，这些运动中，以升沉运动对钻探或其他海上作业影响最大。钻井过程中，钻头要求保持相对恒定的钻压；隔水管与水下BOP的对接过程中，也要求缓慢接近。升沉补偿装置的作用即是对钻井船/平台的升沉运动进行补偿，尽可能减小管串底部载荷和位移的变化，是海洋油气及勘探作业中的关键设备[1-4]。

升沉补偿装置包括天车升沉补偿装置、游车升沉补偿装置、绞车升沉补偿装置以及快绳/死绳升沉补偿装置。受井架内空间的限制，游车升沉补偿难以实现大载荷补偿；绞车升沉补偿及快绳/死绳升沉补偿装置的钢丝绳磨损严重，工作条件恶劣；在高级别海洋钻井平台中，天车升沉补偿装置应用较为广泛[5-13]。

天车升沉补偿装置安装在井架顶端，不占用平台作业空间，补偿载荷大、补偿精度高，主要有摇摆臂式(如图1)及补偿轮式2种形式[14]。吕岩等[15]人分析认为，因为摇摆臂结构形式可最大限度避免钢丝绳在浮动滑轮上的滑动磨损，优于补偿轮式天车升沉补偿装置。天车升沉补偿装置摇摆臂的设计参数很大程度上会影响最终升沉补偿装置的结构形式和质量。合理的结构是设备长期安全稳定运行的保证，尽可能地减轻海洋平台井架顶部质量对增加平台可变载荷、保障极限工况安全具有重要意义。本文旨在通过对天车升沉补偿装置摆臂机构进行力学分析，建立相应的力学模型。通过算例分析，提出天车升沉补偿装置摆臂设计参数的优化设计方向。

图1 摇摆臂式天车补偿装置

1 计算模型

内绕式摇摆臂天车升沉补偿装置由摆臂总成、浮动天车(补偿轮总成)、导向轮、天车架等组成，该装置的两个极限位置如图2所示。与外绕式摇摆臂天车升沉补偿装置相比，其导向轮外伸幅度较小，结构更为紧凑，对于位于浮动式高耸结构顶端的设备来说，有利于减小结构质量和风载。理想状态下，相对于补偿系统提起的钻杆或隔水管底部，浮动天车(补偿轮总成)为零位移；相对于钻井船/平台，天车架和导向轮为零位移；浮动天车与天车架的相对运动和海床与钻井船/平台的相对运动关系一致。通过摆臂的打开和收缩，在绞车和死绳端之间绳长不变的条件下，可实现浮动天车与天车架间垂直方向的相对运动。

a下极限位置(锁紧位置)

b上极限位置

对图2所示的天车升沉补偿装置进行简化。以导向轮与补偿轮的相对位置、摆臂杆的长度、浮动天车的运动位置为参数，得到以摆臂机构准静态力学分析如图3所示。滑轮轴、轴承及滑轮总重力与钢丝绳拉力相比为小量，计算时省略。

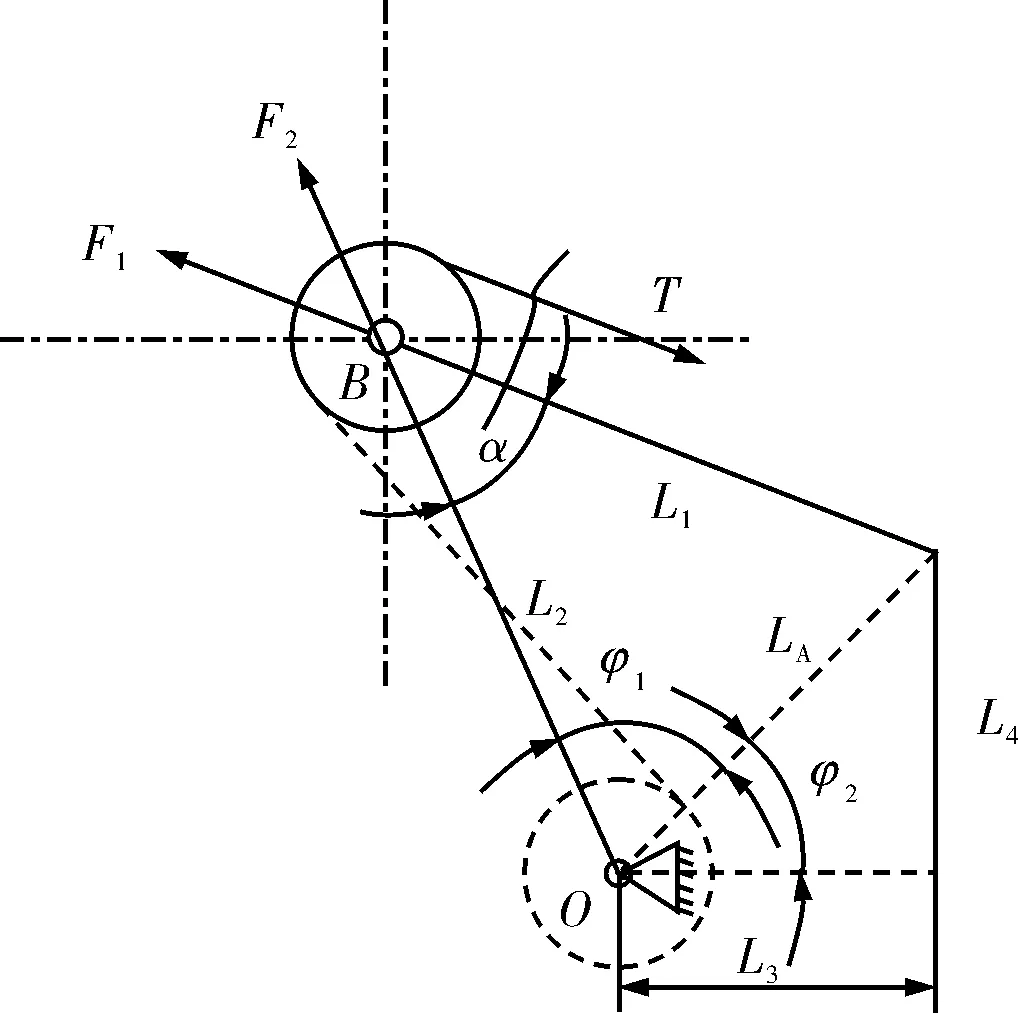
a 下摆杆及力矩平衡b 中间节点力平衡

c 导向轮节点力平衡

从图3可以看出，导向轮、补偿轮以及中间滑轮组成了一个两条边长度确定的三角形，L3长度为初始设计值，L4随浮动天车的运动在一个确定的范围内变化；补偿装置摆臂系统由2个可确定求解的三角形构成。通过力的平衡以及力矩平衡，根据已知参数可求解摆杆上的力F1、F2，导向轮支座反力RR，摆臂打开角度α，以及作用在中间滑轮轴承上的力Fb。

由图3可得：

(1)

(2)

(3)

式中：α为摆臂打开角度，rad；β为两个距离确定的圆切线与圆心连接线之间的夹角，rad。

摆臂关键几何参数确定后，隔离下摆杆，根据力矩平衡求解F1可得：

F1=T·R+T·(R+L2·sinα)/(L2·sinα)

(4)

隔离中间节点，根据节点平衡计算F2可得：

F2=T·sin(α-β)/sinα

(5)

隔离导向轮节点，根据节点平衡计算支座反力RR:

(6)

(7)

其中：φT=φ1+φ2+β。

式中：φ1为上、下摆臂形成的三角形在导向轮处的夹角；φ2为导向轮、补偿轮连线与水平方向的夹角，[0, π/2]；φT为导向轮上部钢丝绳上张力与水平方向的夹角，[π/2, π]，T为快绳拉力，kN。

2 优化算例

900 t天车升沉补偿装置最大补偿载荷为4 500 kN，采用7×8绳系，钢丝绳在主滑轮上缠绕半径R=862.5 mm。升沉补偿行程为7 620 mm(25英寸)。快绳效率系数依照API RP 9B，取值为0.685[16]。

补偿工作状态下，结构额定载荷为4 500 kN，快绳拉力为：

假设快绳拉力在整个补偿过程中为恒定值。L3设计值取2.4 m，L4在下极限位置设计值取1.6 m，L1、L2基本设计值取5 m，极限长度取7.4 m。在L1、L2长度变化时，可得到浮动天车在任何位置摆臂以及轴承上的作用力变化趋势，如图4～5所示。

图4 上摆杆长度变化对各关键部件受力影响

从图4可以看出：①当补偿轮由锁紧位置上升至最高位置的过程中，作用在上摆杆上的力变化幅度较小，作用在中间轴承的力变化较大，先缓慢降低再迅速增大，最大达到1 600 kN；上摆杆中的载荷明显大于下摆杆。②上摆杆长度的初始增长明显降低了各部件的应力水平，当L1=6.6 m时，整个浮动天车运动过程中，作用于中间轴承上的力减小至1 200 kN水平，但是当L1从6.6 m开始继续增长时，在浮动天车下极限位置附近 中间轴承及导向轮轴承载荷有明显增长，即上摆杆继续加长的有利效果消失，不利效果开始出现。③无论上摆杆长度如何变化，整个浮动天车运动过程中，作用在上摆杆上的力始终大于下摆杆，二者最接近时，上摆杆中载荷约等于下摆杆中的两倍；中部轴承载荷明显大于导向轮轴承，二者之间关系也接近两倍。

从图5可以看出，下摆杆长度的增加同样可以明显降低各部件的载荷水平，且在下摆杆增长至7.4 m的长度时，作用于中间轴承上的力达到最小，仅为1 100 kN，相对于初始1 600 kN降幅达到30%以上，更优于上摆杆增长的效果；下摆杆L2=7.4 m时，导向轮轴承上的力在整个浮动过程中变化率很小，较为稳定；上摆杆和下摆杆二者载荷最接近时，上摆杆上的载荷约为下摆杆的二倍。

3 结论

1) 以摆臂的长度为主变化参数，对内绕式摇摆臂天车升沉补偿装置进行了建模和实例分析，得到了上摆臂、下摆臂、中间轴承、导向轮轴承上载荷随浮动天车位置的变化趋势。所提供的建模方法可供未来天车升沉补偿装置设计参考。

2) 相对于上、下摆杆等长的设计方案，上摆杆或下摆杆单独加长均有利于减小摆杆、轴承中的载荷；且下摆杆长度增加对于减小各部件内载荷的效果更加明显。

3) 上摆杆中的载荷明显大于下摆杆中的载荷，在浮动天车浮动的全范围里，上摆杆内载荷最小值约为下摆杆内最大值的两倍。

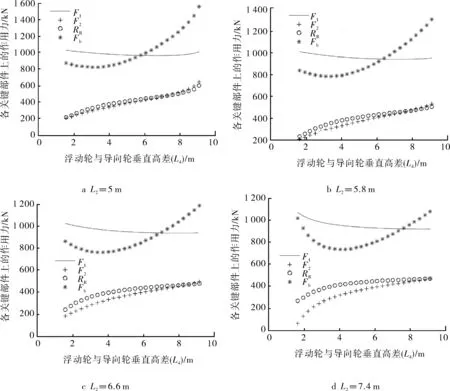
图5 下摆杆长度变化对各关键部件受力影响

4) 在摆杆设计时，由于轴承安装位置限制，上、下摆杆截面抗弯刚度不同，而抗弯刚度和杆长均为影响摆杆受压稳定性的关键参数。摆臂机构可设计为上臂相对短粗、下臂相对细长的结构，可最大程度达到各部件结构应力的均一化，提高材料利用率，减轻设备质量。