基于排队论的鼠浪湖铁矿石码头泊位布局优化研究

汪士寒，张丽娜

(1.宁波财经学院国际经济贸易学院，浙江宁波 315175；2.浙江海洋大学港航与交通运输工程学院，浙江舟山 316022)

科学合理的码头泊位数量布局是提升港口竞争力的一个重要方面，泊位数过剩会造成岸线资源浪费和费用成本上升，泊位数不足会导致到港船舶靠泊等待时间过长使港口失去市场吸引力。鼠浪湖码头占有全国可靠泊40万t级矿石船的7个泊位中的2个，是世界第一大港宁波舟山港的铁矿石集疏运系统中最重要的码头，也是国内最大的铁矿石中转码头和国家最重要的铁矿石储备中转基地之一。但随着铁矿石吞吐量的日益增长，码头泊位数量配置问题凸显。笔者根据码头吞吐量的近期实际和远期预测，利用排队论模型，在岸线资源容量、航道通航能力上限之下，以港、船双方发生和损失的综合费用最小为目标，对鼠浪湖码头泊位数量布局优化问题进行研究，以期为鼠浪湖铁矿石码头的规划发展提供科学依据。

1 研究思路与分布检验

1.1 研究原理与思路

船舶到港分布是一种典型的随机分布，泊位是服务机构中的服务台，船舶和泊位构成了一个排队系统。船舶到港后排队靠泊接受服务属于排队论中描述的排队现象的一种，确定码头的最优泊位数适用排队模型。

港口排队服务系统中，不同的输入过程、排队规则和服务机构适用不同的模型，符合港口服务系统的模型主要有M/M/S和M/Ek/S。在等待制的排队规则下，当船舶到港和占泊服务时间服从泊松分布和负指数分布时，适用M/M/S模型；当船舶到港和服务时间服从泊松分布和K阶爱尔朗分布时，适用M/Ek/S模型[1-2]。

等待制规则：不考虑因其他因素使船舶中途退出的情况，船舶排队队长无限制，泊位对于待泊船舶采用先到先服务原则，泊位一有空闲，船舶立即前去停靠，并且在港的每艘船舶早晚都会服务到。

港口系统的排队规则属于等待制，因此本文在判别鼠浪湖码头船舶到港与占泊时间的分布属性的基础上选用适用的模型，根据码头吞吐量的近期实际和远期预测，在综合费用最小的目标和资源限制的约束下，得到鼠浪湖码头泊位近期与远期的最佳数量配置。

1.2 码头设施与资源

1.2.1 码头泊位与基础设施

宁波舟山港鼠浪湖码头2016年建成投入营运，目前在营泊位5个，其中2个30～40万t级，1个10万t级和2个5万t级(详见表1)。码头现有5台卸船机和2台装船机，卸船机额定能力3 000 t·h-1，装船机额定能力为 7 500 t·h-1。

表1 鼠浪湖码头泊位情况Tab.1 Berth situation at Shulanghu wharf

1.2.2 航道现状与通航能力上限

鼠浪湖码头位于蛇移门水道东部，其所用航道有南、北向主航道及其支航道，航道水深25.1 m，可满足进出本码头船舶安全航行要求(详见表2)。

表2 鼠浪湖码头蛇移门航道情况一览表Tab.2 A list of the status quo of Sheyimen waterway at Shulanghu wharf

1.2.3 岸线资源上限

根据舟山市港航管理局《舟山港域码头设施与资源报告》，鼠浪湖岛拥有岸线16.03 km，其中水深25 m以上岸线1.8 km，可建(30～40)万t级泊位4～5个；水深15 m以上岸线1.9 km，可建10万t级左右泊位5～6个；另有5万t级以下泊位8个左右的建设空间。

1.3 分布检验

多年来国内外大量资料和学者研究证实船舶到港和服务时间服从泊松分布和负指数分布[3-4]。为严密起见，这里根据船舶的到港信息用χ2检验来验证该港口船舶到港和占泊服务时间服从泊松分布和负指数分布。

式中，g 为样本总体 X 实数轴上所取得等距区间数(-∞，t1)，(t1，t2)，……(tg-1，+∞)；n 为到达港口的船舶数；fi表示频数，即样本中 x1，x2，x3，…，xn 发生在第 i段区间的个数(i=1，2，3，…，g)，其对应的频率是 fi/n；pi是频率fi/n将发生在第i段区间上相应的概率，其对应的理论频数为Fi=npi[5]。

用n(t)表示在时间间隔t内到达船舶的数量，则当船舶到达符合泊松分布时，在时间间隔t内到达n(t)艘船舶的概率P可以表示为：

式中：λ表示平均到达率，即单位时间间隔内平均到达的船舶数。μ表示单位时间间隔内单个泊位完成装卸服务的船舶数，即泊位的平均服务率。

鼠浪湖码头是以铁矿石运输为主的装卸中转码头，实际可利用装卸作业的泊位有5个。2018年鼠浪湖码头到港的铁矿石船舶共1 224艘，船舶平均装卸量40 866 t·艘-1。

据码头所在地港航气象统计，鼠浪湖码头建成以来虽然遇到的台风等天气较多，但无大破坏力的极其恶劣天气，港口营运天数为365 d，这样船舶日平均到达率λ=1 224/365=3.353 4艘·d-1。

根据鼠浪湖码头统计数据计算得出单个泊位的平均装卸一艘次船的时间为1.17 d，则μ=1/1.17=0.85艘次·d-1。统计1 d内实际到达船舶的经验频数fi(i=0，1，2，3…10)，由此计算出1 d内船舶到达的经验频率。根据公式(2)求得符合泊松分布一天内到港船舶 1，2，3，…，9，10 艘的理论频率 pi(i=1，2，3….10)，再求出相应的理论频数Fi。计算结果如表3所示。

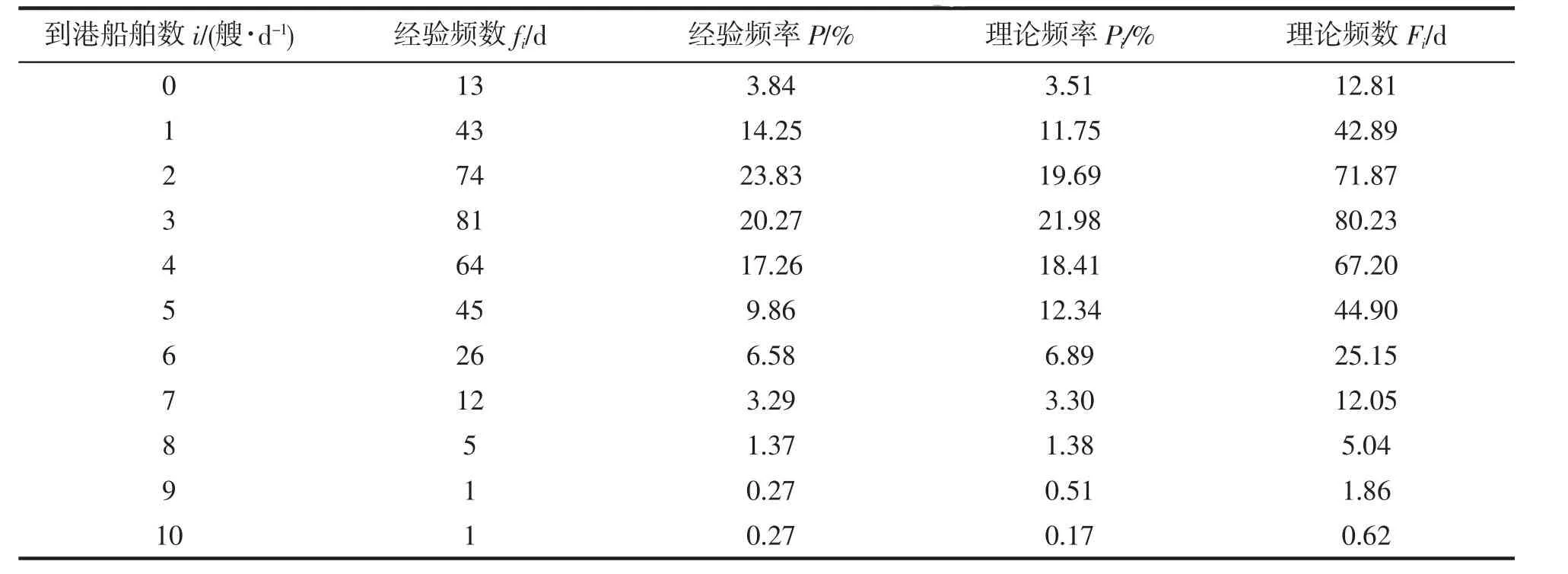
表3 各个参数计算结果Tab.3 Calculation results of each parameter

根据表3数据运用χ2检验来判断鼠浪湖码头船舶到港是否服从泊松分布。

(1)建立原假设H0：船舶到港服从泊松分布。

(2)将表中数据代入公式(1)(g=9组，将理论频数≤5的合并为一组)，求得χ2=2.70

自由度 v=9-2=7，取 α=0.05，查 χ2分布表得 χ20.05=14.067

(3)得出结果χ20.05≥χ2，可知原假设成立，鼠浪湖码头船舶到港服从泊松分布。且实际到港的船舶相继达到的时间间隔相互独立，占用泊位服务时间服从负指数分布。

2 基本模型

分布检验证明输入过程和服务时间服从泊松分布与负指数分布，适用M/M/S模型。

2.1 排队模型

设泊位数为S，在平均到达率λ不变时，当到达船数n＜S时，系统的平均服务效率μ会随着到达船数的增加而发生改变μ、2μ、3μ……(S-1)μ，当到达船数n≥S时，最多有S艘船舶接受服务，n-S艘船舶待泊，平均服务效率保持临界值Sμ不变[6]。

图1 M/M/S排队系统的状态转移图Fig.1 State transition diagram of M/M/S queuing system

如图1所示，从状态(1)转移为状态(0)表示当系统中只有一艘船舶接受服务并离开的转移率为μP1，从状态(2)转移到状态(1)表示系统中有两艘船在泊位接受服务，其中一艘船接受服务完毕离开的转移率为2μP2，以此类推得到稳态状态下系统的方程组：

用递推法求解方程得稳态状态下无船在港的概率P0[7]

《菜根谭》中有言：冷眼观人，冷耳听语，冷情当感，冷心思理。处世“冷”一点，遇事“静”一点，才不会赶走好运气。

有n艘船在港的概率Pn·S

2.2 费用模型

本研究优化目标涉及相关费用，推算费用模型如下：

式中，Tb为泊位年总费用；Ts为船舶在港年总费用；T为船、港年总费用；cb为泊位日均营运费用；cs为船舶日均在港待泊费用；Cb为泊位年闲置费用；Cs为船舶年待泊损失费用；ρs为泊位数为S的泊位利用率；N为365 d。

3 优化计算

3.1 近期优化

鼠浪湖码头当前有关数据：单个泊位的平均装卸时间是1.17 d·艘-1；单个服务台的平均服务率μ=0.85；日均到达率λ=3.35艘·d-1；cb可近似估算为投建泊位的成本和港内动力照明费用、码头设施修理费用、设施折旧费用等部分的花费均摊到单个泊位的费用总和[8]，经综合加权取平均值得cb=21.20万元；根据实际到港船型的平均情况调研与计算得cs=26.48万元。应用前述的模型，计算得到相关数据如表4和表5所示。

表4 M/M/S模型最优泊位数计算结果Tab.4 Optimal berth number calculation results by M/M/S model

表5 不同泊位数产生的泊位闲置损失费和船舶待泊损失费用计算结果Tab.5 Calculation results of berth idle loss and berth waiting loss incurred by different

由表4和表5可以看出泊位数越多，Ts和Cs越低，但Tb和Cb越高，因此，码头在规划泊位时不能盲目建设，要科学规划泊位数。

由表4和表5可知，当泊位数S=6时，发生在港、船双方的综合费用T的值最小，双方的综合损失费用也最小。因此，当前鼠浪湖码头需要增加1个泊位，这样效益最佳，一年可降低费用6 347.42万元。根据未来铁矿石船型大型化趋势，鼠浪湖码头近期可增加1个(10～30)万t级的泊位。

3.2 远期优化

远期优化需要对鼠浪湖码头的远期吞吐量进行预测。由于鼠浪湖码头营运的时间不久，无法得到足够的铁矿石吞吐量数据样本来进行预测，这里拟根据整个舟山港域铁矿石吞吐量预测及近几年鼠浪湖码头吞吐量占比分析推算鼠浪湖码头铁矿石的吞吐量预测值。

根据舟山港域铁矿石码头2006-2018年铁矿石吞吐量数据，利用二次指数平滑预测和灰度预测所构建的组合模型，在假定未来几年内经济结构与需求趋势不发生较大改变的前提下，预测舟山港域铁矿石2025年吞吐量约为22 743万t(篇幅限制，详细预测过程略)。

鼠浪湖铁矿石码头自2016年建成营运以来，由于其定位与硬件条件，其吞吐量在整个舟山港域铁矿石吞吐量的占比快速增加(表6)。而这几年中，港域内内其他铁矿石码头占比则主要在下降。

表6 2016-2018年鼠浪湖码头铁矿石吞吐量占比Tab.6 Proportion of iron ore throughput of Shulanghu wharf in 2016-2018

根据鼠浪湖码头从2016年投运至今的历年吞吐量与其它矿石码头历年吞吐能力的平衡分析，考虑码头现有岸线与航道资源容量上限，结合专家评估意见和政府规划，推算2025年鼠浪湖码头的铁矿石吞吐量将占舟山港域总吞吐量35%左右，约为7 960万t。

3.2.2 远期优化计算

已知当前泊位的年设计通过能力为5 200万t·a-1，预测2025年的铁矿石吞吐量为7 960万t，产生2 800万t左右的能力缺口，因此需要增加泊位。设每台装卸机械的装卸效率依然是3000 t·h-1，船舶在本港的平均装卸量参照2018年的40 866 t·艘-1，营运期N=365 d，此时的船舶到达率λ=5.34艘·d-1，以S=7，8，9，10，11来进行测算，计算结果如表7、表8所示。

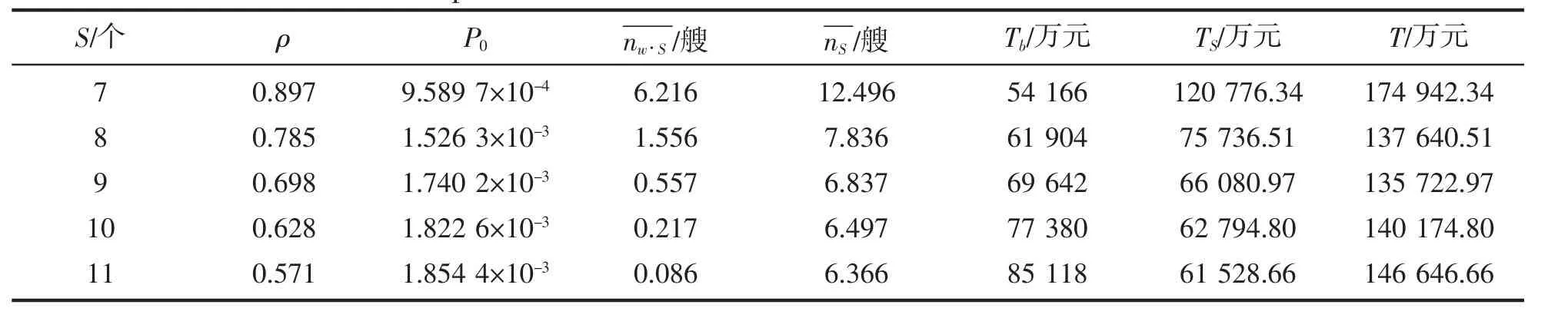
表7 M/M/S模型最优泊位数计算结果Tab.7 Optimal berth number calculation results by M/M/S model

表8 不同泊位数产生的泊位闲置损失费和船舶待泊损失费用计算结果Tab.8 Calculation results of berth idle loss and berth waiting loss incurred by different berths

结合表7、表8中的计算结果可以看出，当泊位数S=9时，发生在船、港双方的综合费用T和船、港方综合损失费用Cb、Cs最小，鉴于现有泊位为5个，因此需要增加4个泊位。

根据未来铁矿石船型大型化趋势，远期可考虑增加4个10～30万t级的泊位，泊位年设计吞吐能力达到 8 000 万 t。

4 结论

(1)鼠浪湖铁矿石码头排队系统中，船舶到港和占用泊位服务时间服从泊松分布和负指数分布，适用M/M/S模型。

(2)以综合费用最小为优化目标，经优化计算，当前鼠浪湖码头泊位数量布局不能满足要求，需要增加1个泊位，这样每年可节省6 347.42万元，使本港的效益最大化。综合考虑未来铁矿石船型大型化趋势，鼠浪湖码头近期可考虑增加1个(10～30)万t级的泊位。

(3)在假定未来几年舟山港域腹地经济结构和需求趋势不发生较大变化的情况下，预测2025年舟山港域铁矿石吞吐量为约为22 743万t，鼠浪湖码头的铁矿石吞吐量将占舟山港域总吞吐量35%左右，约为7 960 万 t。

(4)按上述预测值，鼠浪湖码头未来(2025年前)泊位数量布局需要进一步优化，在综合费用最小原则下其泊位数量为9个。根据鼠浪湖码头吞吐量预测以及铁矿石运输船型分析，2025年之前需增加4个(10～30)万t级的泊位，码头年设计吞吐能力需达到8 000万t，以满足对铁矿石运输的要求。