单线铁路隧道地震作用下台阶法支护的动力响应分析

李仁强

摘要：在地震高烈度区隧道设计都会按照规范要求考虑地震作用的影响，然而常常会忽略施工过程中地震作用对隧道施工安全的影响。因而，论文以单线铁路隧道台阶法施工为例，通过弹塑性数值分析，获得台阶法施工过程的关键施工步。在此基础之上，考虑关键施工步阶段发生地震，对该阶段进行动力分析。结果表明，台阶法施工中，下台阶开挖为关键施工步;围岩的拱顶下沉受地震影响较大，边墙的水平位移受地震影响相对较小;上台阶初期支护应力受地震影响较大，但是最大拉应力约为2.2MPa，最大压应力没有超过16 MPa。考虑地震作用下的应力较未考虑地震作用时大，因此，在高烈度地震区的隧道设计和施工均应考虑地震对隧道施工安全的影响。

Abstract： The tunnel design in the high-intensity seismic zone generally considers the impact of seismic action according to the normative requirements. However， the impact of seismic action on tunnel construction safety is often neglected. Through the elastoplastic numerical analysis， the key construction steps of the Benching Tunnelling method are obtained. On this basis， assume that the earthquake happened in the key construction step， and carry out dynamic analysis on this step The results show that in the Benching Tunnelling method， the key stage is the excavation of the lower step. The subsidence of the arch of the surrounding rock is greatly affected by the earthquake， and the horizontal displacement of the side wall is born affected By the earthquake; the support stress of the upper step in the initial stage is greatly affected by the earthquake， but the maximum tensile stress is approximately 2.2 MPa， and the maximum compressive stress does not exceed 16 MPa. Since the stress under earthquake is larger than the stress without an earthquake， the tunnel design and construction in the high-intensity seismic zone should consider the impact of an earthquake on tunnel construction safety.

關键词：地震;软质板岩;大变形;台阶法

Key words： earthquake;soft slate;large deformation;benching tunnelling method

中图分类号：U455                                         文献标识码：A                                  文章编号：1006-4311（2019）17-0127-07

0  引言

地震对隧道结构的损害较地面结构小，对于高地应力软弱岩体隧道施工，隧道变形控制原则应以应力释放与支护抗力相结合为基础[1-2]。对不同边界的隧道模型进行动力计算表明，围岩应力值受边界取值范围影响小，围岩位移值受底边界取值范围影响大;并且地震动力计算边界取较大宽度时，围岩应力及位移受边界取值范围影响可以忽略[3]。蒋树屏等[4]根据大量震害资料的调查分析发现，地下结构埋置深度对其地震破坏程度影响很大。李林等[5]通过振动台模型试验及数值计算分析表明偏压隧道有较不利的内力值分布与较大峰值。梁建文等[6]采用黏弹性边界方法和地震动输入等效节点力方法，建立地铁隧道地震响应分析问题的模型。刘妮娜等[7]通过振动台模型试验表明扩大断面的马蹄形隧道结构中拱腰部位的应变增值最大，拱顶部位次之，底板的应变增值相比最小。Haitao Zhu等[8]研究表明隧道周围不同位置土体在竖向地震作用下具有较大的相对位移。王国波等[9]基于土体-隧道群相互作用的分析表明，隧道半径、埋深和空间间距对场地土和隧道的地震响应显著。崔光耀等[10]通过建立三维有限差分数值模拟和现场震害分析表明震害主要发生在软硬围岩交接处，主要影响因数为强制位移，地震惯性力次之。地震对隧道结构的影响已有大量的研究，但隧道施工过程中考虑地震作用的研究成果还不完善。本文依托杰德秀一号隧道通过建立数值模型，探究地震作用下台阶法关键施工步的围岩支护动力响应。

1  依托工程概况

杰德秀1#隧道位于青藏高原东南部雅鲁藏布江左侧山南地区贡嘎县，进口里程为DK59+860，出口里程为DK61+550，全长1690m，最大埋深约190m。根据《中国地震动参数区划分图》（GB18306-2001图A1，1/400万）（含GB I8306—2001《中国地震动参数规划图》国家标准第I号修改单）及《川藏铁路拉萨至林芝段工程沿线断裂活动性评价及地震动参数区划报告（修改稿）》（国家地震局地质研究所2013年4月），地震动峰值加速度为0.15g;动反应谱特征周期值为0.65s。

分析断面掌子面围岩为绢质板岩、石英砂岩互层，层间有少量黄色粉土物质，层间结合较差，岩石节理裂隙发育，有掉块及小规模坍塌发生。支护参数为：预留沉降量为10cm，初支为厚度25cm的C25喷混凝土，采用I18型钢拱架，每榀间距0.8米，拱墙采用Ф22组合中空锚杆L-5m，二衬厚度45cm，C35钢筋混凝土;仰拱衬砌厚度45cm，C35钢筋混凝土，仰拱填充采用C20混凝土。

2  台阶法关键施工步序分析

2.1 计算参数和模型

围岩及支护的计算参数参照新建铁路川藏线拉萨至林芝段施工图等资料，根据参考文献[11]的研究成果，在计算中将系统锚杆支护区域的岩体的弹性模量、粘聚力及摩擦角提高30%作为其加固效果，本文主要通过弹塑性分析来获得台阶法关键施工步序，计算所需的参数见表1。

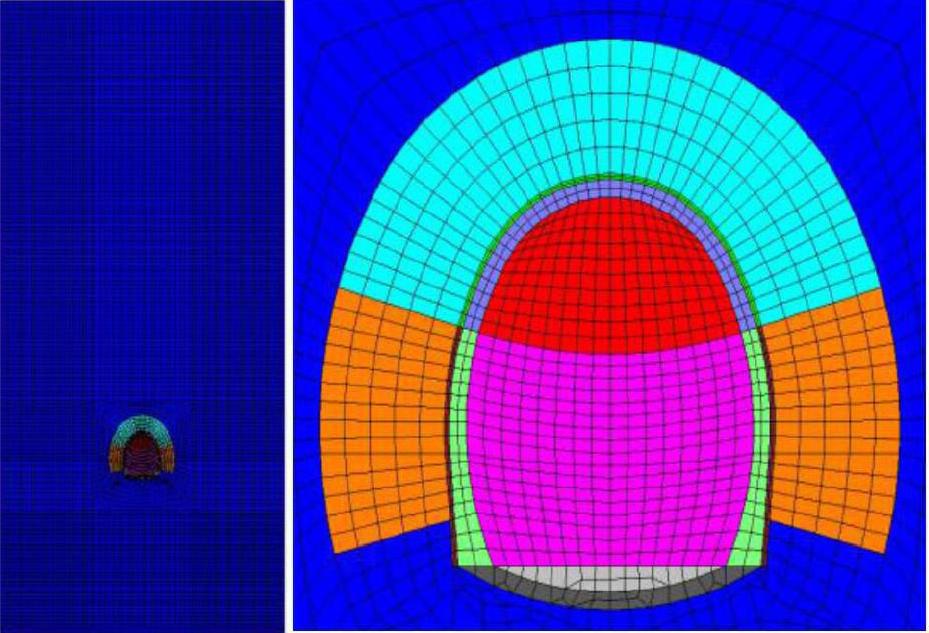
该断面埋深84.5m，模型顶部取至地表，左、右及下边界都取三倍洞径。整个模型大小为120m（高）×65m（宽），13556个单元，27574个节点。围岩、加固区、喷射混凝土及二衬均采用实体单元。边界条件：顶部为自由边界，底部施加竖向约束，前后左右均施加法向水平约束，计算模型如图1。

2.2 分析步骤

依托工程为单线隧道，采用台阶法施工，分析步骤一共八步（见表2）。计算中仅考虑重力作用下的初始应力，上台阶初期支护和下台阶初期支护包括喷射混凝土、锚杆施作和架设工字钢。

2.3 结果分析

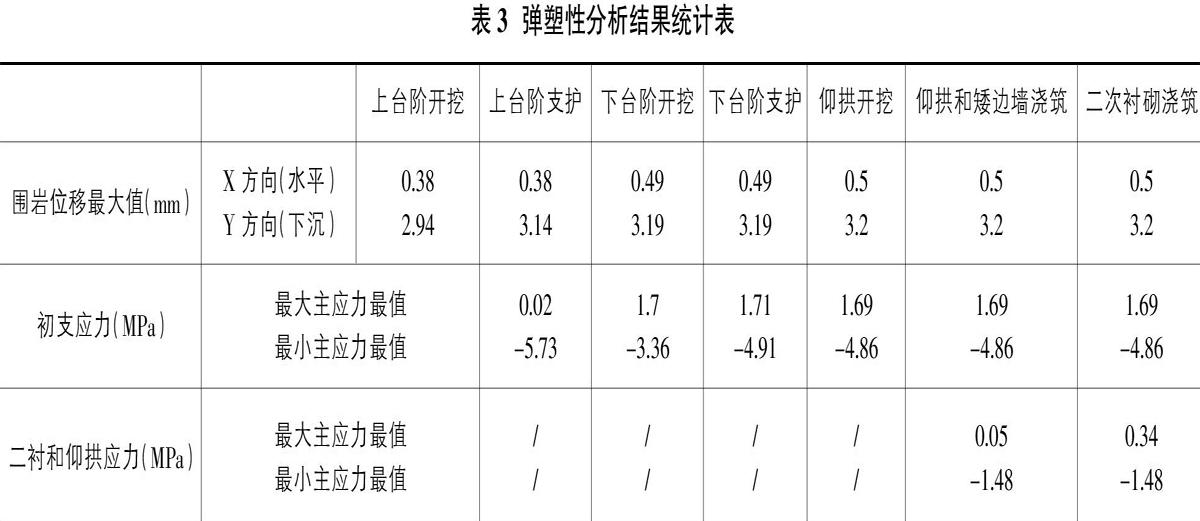
通过弹塑性数值分析，获得了各施工阶段的围岩位移、初期支护应力、仰拱应力及二次衬砌应力（见表3）。由表3可知，下台阶开挖后，围岩的最大水平位移和拱顶沉降分别为0.49mm和3.19mm。初期支护的最大主应力1.7MPa。在二次衬砌没有完成之前，围岩变形和初期支护第一主应力都非常接近施工过程的最大值，因此下台阶开挖是台阶法施工过程中安全控制的关键施工步。

3  地震作用下围岩及支护响应

3.1 地震分析边界条件

上述分析表明单线隧道使用台阶法施工时，无论是围岩变形还是初期支护的受力状态表明下台阶开挖都是最危险的一个施工阶段。因而对最危险阶段进行地震动力分析，对施工过程中遭遇地震时，分析结果对类似工程具有较强的指导作用。本文研究采用时程分析法，地震曲线采用EL CENTRO波（见图2）。首先将原始EL波进行处理，将最大值振幅控制在2。由图2可知，最大振幅出现在前5s内，在只考虑最不利的前提下，只需将最大振幅包含在计算时间内即可，因而本研究仅计算前5秒。

数值计算模型仍使用上文分析的模型，此处仅对下台阶开挖完成后进行动力分析，边界条件有所不同。动力边界条件：顶部为自由边界，前后左右均施加法向水平约束，释放底部约束，施加动力边界条件。此处动力边界为加速度时程曲线，依托工程的场地条件为0.15g，因而施加在模型底部的实际最大加速度振幅为2×0.75=1.5m/s2。

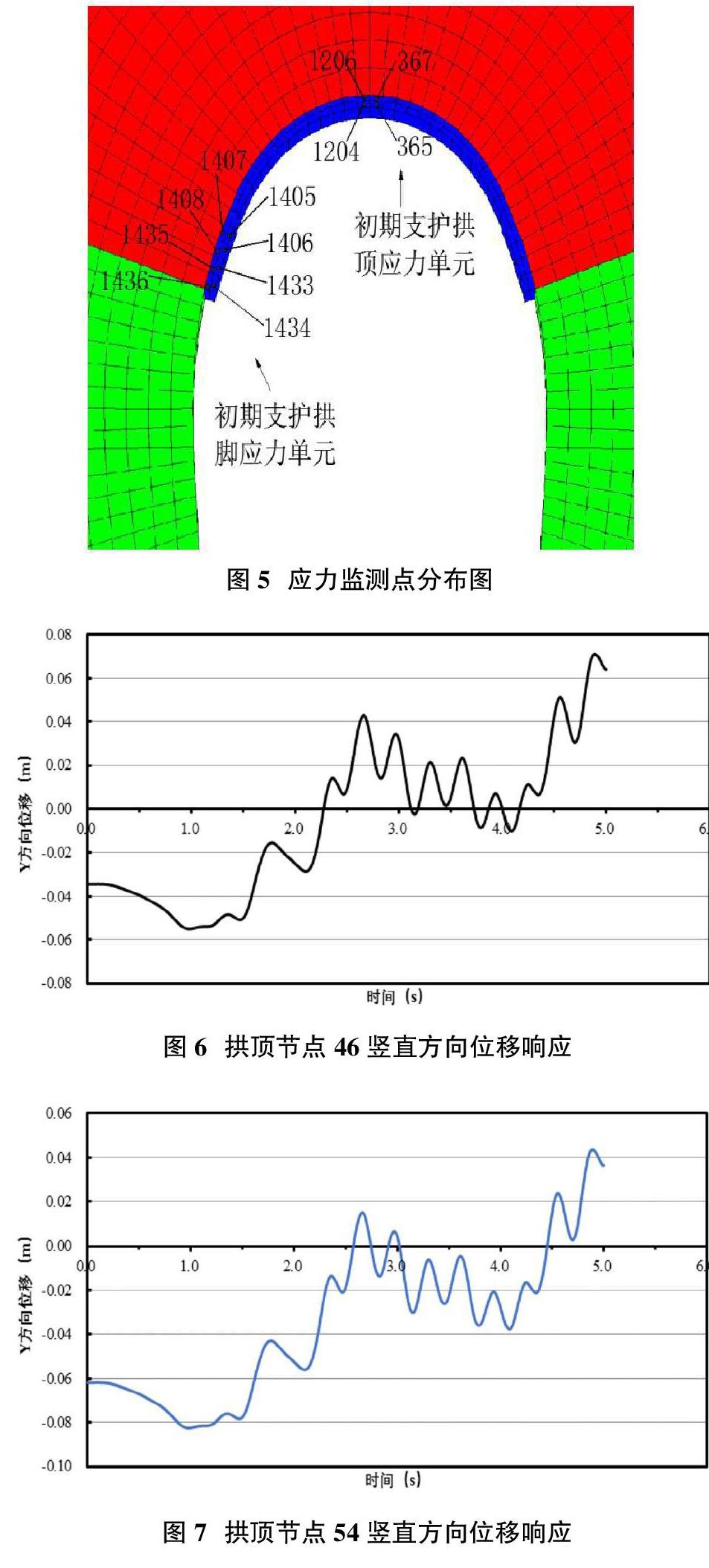
围岩变形最大出现在拱顶、边墙下部、底部中心及初期支护下边界处，因此，研究对节点54、46、255、113、508、301、321、311、309等的水平位移和竖直位移进行分析，这些点在数值模型中的位置见图4。初期支护的应力在拱顶和拱脚较大，因而监测了拱顶和拱脚的部分单元的最大主应力和最小主应力的分布，数值模型中单元编号分别为：365、367、1204、1206、1405、1406、1407、1408、1433、1434、1435、1436，它们的位置见图4。

3.2 围岩位移响应

前面分析可知，拱顶的竖直位移变化较大，因而此处主要研究了拱顶中心三个节点的竖向位移对地震的响应，分别是节点46、和节点54，其位置见图4。根据前面得到竖直位移分布，节点46在-6～8cm之间变化，而节点54在-8～5cm之内变化。以预留变形量作为标准，则拱顶竖向位移在控制范围之内。

为了获得边墙下部水平位移变形最大的位置和变形情况，根据前面得到水平位移分布，在上版断面左右各选取了一个节点，节点113、节点255进行分析。在边墙的下部选择五个节点的水平位移进行了分析，分别是节点301、节点309、节点311、节点321，其位置见图4。节点113和节点255的水平位移变化基本一致，随时间增加水平位移值有增加趋势，但是总体来讲都在1cm以内，变形较小。边墙变形规律基本一致，振幅基本在4cm以内。

3.3 初期支护应力响应

前面分析可知，初期支护拱顶所受压应力较大，因而此处主要研究了拱顶初期支护的应力对地震的响应，分别选取了单元365、单元367、单元1204和单元1206进行了分析，其位置见图5。四个单元的最大主应力和最小主应力随时间变化如图14-图21。从最大主应力变化可以看出，这四个单元都没有出现拉应力，振幅较大，均在0.6MPa以内。由最小主应力变化可知，拱顶初期支护下边缘所受压应力大于上边缘单元，振幅在-4～-17MPa之间。相对于最大主应力来讲，最小主应力变化相当大。

前面分析可知，初期支护拱脚所受拉应力较大，因而此处主要研究了拱脚初期支护的应力对地震的响应，分别选取了单元1405、单元1406、单元1407、单元1408、单元1433、单元1434、单元1435和单元1436进行了分析，其位置见图5。八个单元的最大主应力随时间变化如图22-图29。从最大主应力变化可以看出，初期支护外侧拉应力较小，变化相对内侧较小;单侧四個单元的中间单元拉应力较大，两端较小;单元1408的最大拉应力达到约2.2MPa，没有超过等效强度，不影响初期支护安全的水平。

八个单元的最小主应力随时间变化如图30-图37。从最小主应力变化可以看出，单元1405和单元1406的压应力变化最大，最大压应力超过10MPa，但是最大值没有超过16MPa，没有超过等效强度，不影响初期支护安全的水平。

4  结论

本文通过单线铁路隧道台阶法施工为例，考虑地震作用对关键施工步安全影响分析，得到以下结论：

①下台阶开挖完成之后，围岩变形和初期支护第一主应力都非常接近施工过程的最大值，因此下台阶开挖是台阶法施工过程中安全控制的关键施工步。

②下台阶开挖完成后考虑地震作用时，拱顶下沉受地震影响较大，振幅在8cm左右，水平位移受地震影响相对较小，位移振幅在4cm以内。

③上台阶初期支护的应力受地震影响也较大，最大拉应力约为2.2MPa，最大压应力没有超过16MPa。考虑地震作用下的应力较未考虑地震作用时大，因此，在高烈度地震区的隧道设计和施工均应考虑地震对隧道施工安全的影响。

参考文献：

[1]Chengyong Cao，Chenghua Shi， Mingfeng Lei，Weichao Yang，Jianwen Liu. Squeezing failure of tunnels： A case study[J]. Tunnelling and Underground Space Technology incorporating Trenchless Technology Research，2018，77.

[2]Chengyong Cao， Chenghua Shi， Mingfeng Lei， Weichao Yang，Jianwen Liu. Squeezing failure of tunnels： A case study[J]. Tunnelling and Underground Space Technology incorporating Trenchless Technology Research， 2018，77.

[3]袁松，王峥峥，周佳媚.隧道地震动力计算边界取值范围研究[J].土木工程学报，2012，45（11）：166-172.

[4]蒋树屏，方林，林志.不同埋置深度的山岭隧道地震响应分析[J].岩土力学，2014，35（01）：211-216，225.

[5]李林，何川，耿萍，曹东杰.浅埋偏压洞口段隧道地震响应振动台模型试验研究[J].岩石力学与工程学报，2011，30（12）：2540-2548.

[6]梁建文，于军港，张季，巴振宁.基于黏弹性边界的地铁双隧道地震响应分析[J].土木工程学报，2014，47（S1）：274-279.

[7]刘妮娜，彭建兵，韩冬冬，黄强兵，门玉明，石玉玲.穿越活动地裂缝地铁隧道震害机制研究[J].岩石力学与工程学报，2015，

34（07）：1384-1391.

[8]Haitao Zhu， Tianjiao Tang，Puyang Zhang，Jianqiao Sun.Random Vibration Analysis of Urban Underground Tunnels Under Vertical Earthquake Excitations Based on Mass–Damper–Spring Model[J].Transactions of Tianjin University， 2018， 24（03）：290-300.

[9]王国波，王亚西，于艳丽，陈斌.土体-隧道群相互作用体系地震响应研究[J].中国公路学报，2015，28（07）：66-76.

[10]崔光耀，刘维东，倪嵩陟，王明年，林国进.汶川地震公路隧道普通段震害分析及震害机制研究[J].岩土力学，2015，36（S2）：439-446.

[11]张学富，周元江，周元辅，周杰.地表荷载对浅埋非对称小净距隧道的影响分析[J].重庆交通大学学报（自然科学版），2018，37（06）：21-27.

作者简介：李仁強（1979-），男，辽宁沈阳人，本科，高级工程师，研究方向为隧道工程、地铁工程。