双障碍期权的定价问题及其近似计算

文/章宏 刘毅，上海大学经济学院

1 引言

双障碍期权有一条上障碍线和一条下障碍线,在其有效期内,一旦标的资产达到上、下障碍线的任一条,期权即被敲进或敲出。张斌（2004）总结Kunitomo and Ikeda(1992)、Geman and Yor(1996)等人结果的基础上根据各种障碍期权所满足的边界条件得出其定价公式模型。然而他得出标的资产价格首达上下边界停时的概率密度公式在实操应用时较为困难。本文对上述公式进行改进，并具体赋值证明改进公式的精确性。

2 文献综述

自1973年美国经济学家迈伦－斯科尔斯（Myron Scholes）与费雪－布莱克（FischerBlack）首创性的提出标准看涨看跌期权定价公式以来，国内外学术期刊关于股票期权定价与其他金融衍生品定价的研究成果枚不胜举。近年来,奇异期权的定价又成为国外期权定价中的热门问题,其中障碍期权是一种重要的奇异期权,又称关卡期权,它是一种弱路径有关期权。它是一张欧式期权合约,其最终收益除了依赖于原生资产在期权到期日的价格,还与原生资产价格在整个期权有效期内是否达到某一规定水平人们称为障碍值有关。在Black-Scholes 环境下，国内外学者发掘出了一系列由普通期权构造组合派生出的奇异期权的定价模型研究。自上个世纪60年代末，市场上开始出现障碍期权后，关于障碍期权的研究如雨后春笋般出现。在障碍期权的定价研究方面，基于Black-Scholes 期权定价框架下，Merton（1973）最早发表了关于障碍期权文章，该文章提出障碍期权的价格就是带边界的 Black-Scholes 方程的解，作者求解出该偏微分方程并分别给出了常障碍和变化障碍水平下的下降敲出看涨期权的定价公式。随着Merton 研究后，Rei nner 和Rubinsteiii(1991)通过一系列公有因子推导出标准障碍期权的的定价公式，依赖于这些公有因子可以分别计算出向上敲出，向下敲出，向上敲入，向下敲入障碍期权的价格，上述这些解析解公式至今仍然是业界使用较为普遍的计算障碍期权理论价格的定价方式。

期权定价理论近几年的发展，已经在传统Black-Scholes 期权定价下扩展到各式期权的理论研究，其复杂程度和计算难度不断加大和精细化。Kyunghyun Park, Junkee Jeon（2017）通过简化来自PDE 的转换变换，应用拉普拉斯- 卡森变换（LCT）讨论了美国敲出期权定价问题。Julien Hok, Tat Lung (Ron) Chan（2018）开发了一种基于一系列密度函数的Legendre 多项式推导出的期权定价公式。解决了因传统公式中数值不稳定造成的欧式看涨期权的精度不够的问题。由于我国资本市场并未完全开放，期权历史发展较短，其研究主要结合国外理论进行扩展研究国内期权市场。总体而言，国内文献对障碍期权产品的研究主要体现在两个方面。一在产品定价研究上，现有的研究主要集中于纯障碍期权产品与内嵌障碍期权的结构化产品上。二在风险管理研究上，现有的文献主要从风险对冲方法和效果比较上进行研究。

3 定价模型

3.1 双敲出期权价值的数学模型

双障碍看涨期权模型,设上下障碍线分别为l1, l2,且0＜l2＜K＜l1,K, l1, l2为常数,K 为期权的敲定价。假定标的资产(股票)的价格在[0,T]时间内向上达到l1或向下达到l2 时,期权自动失效。若股票的价格在[0,T]时间内没有达到l1和l2,则在到期时T,期权的收益为（S(T)-K)+因此,该期权在t 时的价值为：

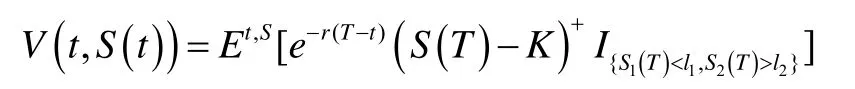
函数V(t,S(t))满足终值条件与边界条件：V(T,S(T))=(S(T)-K)+, l2≤S(t) ≤l1

V(t, l1)=0,V(t, l2)=0 0≤t≤T

3.2 推导的概率密度公式

张斌在总结上面前人结果的基础上在风险中性假设下,从理论上证明了障碍期权价值满足Black-Scholes 方程,再根据各种障碍期权所满足的边界条件得出其定价公式模型。然后他同时对于单曲线边界期权则运用等价鞅测度及变量代换将变边界转化为常数边界,再运用反射原理得出标的资产价格首达边界的分布函数。最后,对双障碍期权,在证明了标的资产价格首达上、下边界的时间期望有界的前提下,运用随机分析有关知识及留数定理得出标的资产价格首达上下边界停时的概率密度。其标的资产价格首达时的概率密度公式如下：

从x 出发首先到达下障碍线0 的概率密度：

从x 出发首先到达上障碍线l 的概率密度：

3.3 首达时的概率密度公式改进

在上述基础上，取l=2π，运用中值定理将无穷项改为两项近似值的和：

其中-1<ρ1<-1，-1<ρ2<1

其中改进公式中的误差项为：

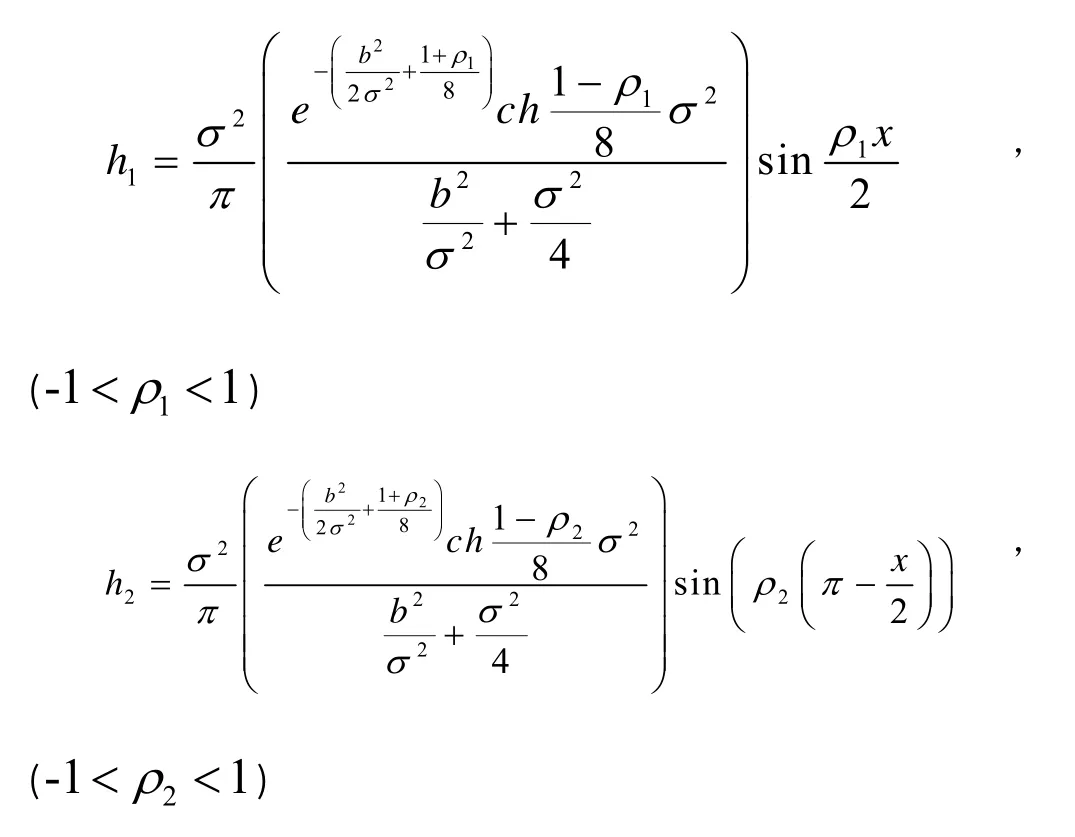
3.4 举例检验

本文主要运用计算机模拟计算原式前N 项和与改进公式的结果作比较，由于改进公式中参数变量较多，只有控制有效变量来观测计算结果才具有可观性，因此本文将N，T 作为控制变量，前N项和逐渐增加来观测原式结果的规律性。T 变化用来观测改进公式的可操作性。具体步骤如下：

检验步骤：（1）赋值：σ=0.02，b=0.002，T 取100、90、80。（其中为了便于无穷项和前N 项变化明显，σ、b 取了特定值，由于0

?

观测表格中第五、六两列的数据表明h1 和h2 可以非常好的近似计算无穷项的和，当N 取到60 项以后，无穷项的和在小数点第十位以前的数值趋于稳定、变化非常小。而我们取ρ1，ρ2等于0.000008665 时，代入h1,h2 计算出结果，h1 和h2 可以精确到小数点后十位。因此改进公式可以近似计算原公式前70 项以后的和且精度达到小数点后十位，误差非常小。

通过上述检验证明，改进公式中ρ1，ρ2的存在唯一性，当σ、b、T、x 给定时，ρ1，ρ2的值唯一确定，改进公式可以非常准确的估计原无穷项和。从而证明改进公式的有效性。在计算期权价值时运用该公式可以规避无穷项的叠加，将复杂的密度公式化简并易于计算。

4 总结

期权交易是指期权持有者拥有在将来某一确定时间或时期内以某一确定价格买卖确定数量的某种资产的权利。本文梳理了前人在期权定价模型上的推导，在根据各种障碍期权所满足的边界条件得出其定价公式模型和标的资产价格首达上下边界停时的概率密度。在双障碍期权的定价中，在标的资产价格首达上、下边界的时间期望有界的前提下，运用标的资产价格首达上下边界停时的概率密度公式进行计算双障碍期权价格时将非常方便。但理论的完备并不能带来实际计算上的简便，而上述的资产价格首达上下边界停时的概率密度公式就因无穷项的叠加困难带来计算上的不便。本文经运用中值定理改进原无穷项的和为两项之和，减少运用上的困难，同时化简两项和为一项（h1、h2）。并经计算机模拟计算发现改进项h1、h2 可以很好的拟合原式的数值。这项工作将给期权定价公式带来实际运用上的快捷性。