车辐式索桁架拉索松弛敏感试验及可靠性评估

刘占省， 韩泽斌， 何 建， 王泽强

(1. 北京工业大学 建筑工程学院， 北京 100124； 2. 哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001；3. 北京市建筑工程研究院有限责任公司， 北京 100036)

车辐式索桁架结构中的索基本都是施加了设计好的预应力值的，但是在实际工程操作或环境影响下势必会造成一定程度的松弛.预应力是结构体系中的一个自平衡力系，如果出现预应力损失，力系必定重新调整达到新的平衡，因此引起一些杆件内力增长，则可能是有害的，危害结构的安全使用.

目前，国内外对于结构预应力损失后的力学性能做了一些研究，郑君华[1]以Geiger和Levy体系索穹顶结构为例，分析了部分索松弛或破断后的受力性能.刘洪波[2]研究了索撑节点处的滑移摩擦对弦支穹顶结构预应力分布的影响.刘占省[3]针对弦支筒壳结构中拉索预应力损失问题，基于可靠度理论进行研究.王树[4]模拟了施工过程中环索预应力损失并分析了预应力损失对弦支穹顶结构的影响.Kristek[5]采用了蒙特卡洛拉丁超立方抽样方法对混凝土箱梁徐变引起的预应力损失进行了可靠性分析.YAN[6]提出一种等效摩擦单元来模拟索杆节点的摩擦，分析了索杆接头的摩擦引起的预应力损失对索支承结构的影响.上述研究大都针对于弦支穹顶、索穹顶空间结构，而对于车辐式索桁架结构拉索发生松弛的研究较少，且在结合试验、修正模型分析拉索松弛和从可靠性评估拉索松弛对车辐式索桁架结构的影响方面研究更少.

本文设计了一跨度为6 m的车辐式索桁架结构模型，并依据张拉成型后试验模型进行三维扫描得到修正理论模型，通过试验数据与理论数值、修正数值对比分析，对车辐式索桁架结构在拉索发生松弛下内力位移变化进行研究，确定其敏感性构件.基于可靠性理论，考虑实际工程中多种因素对拉索发生松弛的影响，运用响应面法和蒙特卡洛法得到拉索发生松弛下的可靠度指标β，得出拉索松弛对可靠度的影响和不同结构参数的灵敏度.

1 模型设计

本试验以某车辐式索桁架结构工程为背景，几何缩尺比例为1∶10，应力比为1∶1.长度和弹性模量的相似系数、为设计时首先确定的条件，针对本试验几何相似系数Sl=1/10 ，模型采用与原结构模型同样的材料 ，所以材料相似系数Se=1/1.从而，模型与原结构模型中拉索、撑杆的截面积比为1∶100.为了满足应力比1∶1的要求，需对结构进行9倍自重荷载的质量补偿，并将质量补偿等效为在节点上施加相应的质量块.

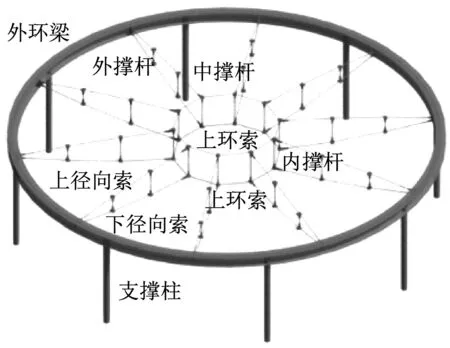
该车辐式索桁架结构试验模型由10榀径向索、两道环索、外环梁和柱子组成，每榀索桁架包括径向索、环索和撑杆，拉索由厂家提供的材性数据为依准，试验模型图如图1所示，模型尺寸如图2所示.为了模拟预应力损失对构件的影响，在径向索索头、环索、撑杆中部设置调节套筒，调节量为±60 mm，试验模型构件规格如表1所示.

试验模型索力通过拉压传感器测量，索力测点布置为：上下径向索每隔一榀布置一个测点，各5个测点，上下环索各布置一个测点，一共12个测点，测点布置图如3所示.

a 设计模型

b 试验模型

图1 车辐式索桁架模型

Fig.1 Spoke cable-truss model

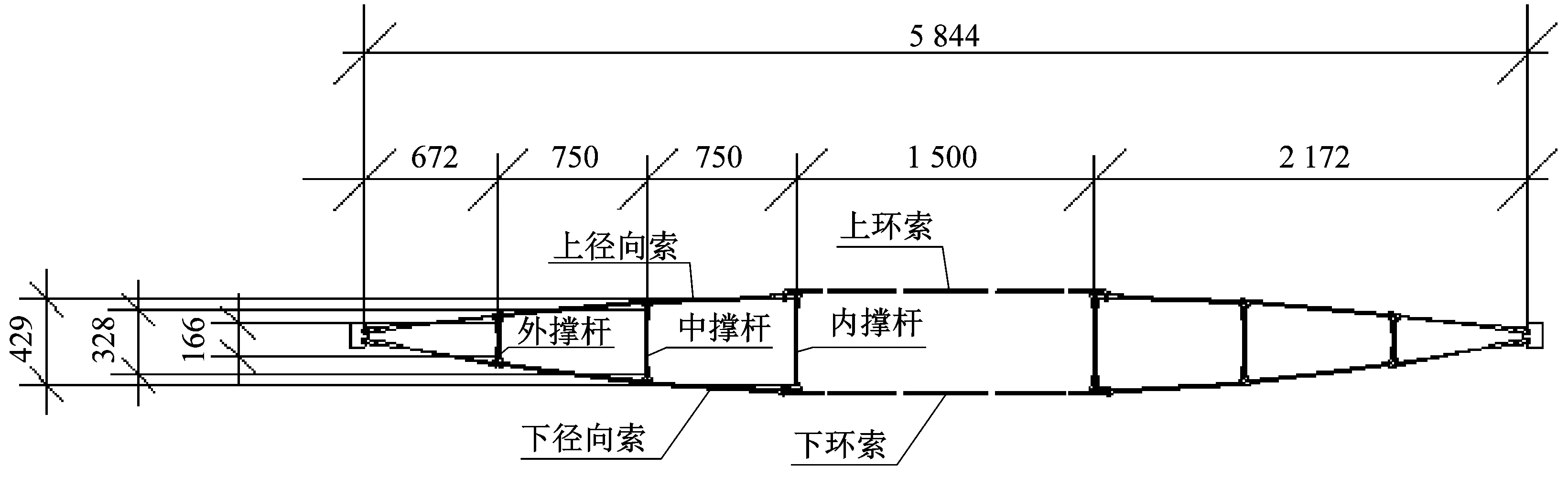
图2 模型尺寸(单位：mm)

表1 试验构件规格

图3 传感器测点布置

2 试验流程

对结构进行张拉，将钢柱、外环梁和斜撑拼装完成，采用张拉径向索方案将结构张拉到位，构件组装和张拉成型图片如图4所示.

a 构件组装

b 张拉成型

考虑到加工误差，安装误差等一些不可控因素，会导致试验数据与理论数据有一定偏差，引入修正模型，在车辐式索桁架张拉完成后，采用三维扫描获取实体试验模型，并根据三维扫描得到的点云模型，点云模型如图5所示.

a 点云模型误差报告

b 获取点云模型

通过点云模型获取对应理论模型的关键节点坐标，依据节点坐标建立修正后有限元模型，由于修正模型排除了加工误差和施工误差对拉索松弛试验的影响，修正模型分析得到的数据更能反应实际试验模型的静力性能.

3 拉索松弛分析

拉索松弛试验中，活荷载取静力加载试验0.5 kN·m-2的三分之一，即0.167 kN·m-2，与正常使用荷载为同一个量级.为了模拟拉索松弛极限状态，按照有限元模拟中施加的预应力的百分比0～100%进行定义.试验分别分析了单根上径向索、单根下径向索、上环索、下环索、全部上径向索、全部下径向索.通过有限元模拟可知单根上、下径向索松弛对结构静力性能影响很小，因此单根上、下径向索进行了有限元模拟中施加的预应力的50%和100%松弛两个工况，其余按照有限元模拟中施加的预应力的20%、40%、60%、80%、100%进行松弛，松弛试验通过调节套筒来控制拉索松弛程度.

为便于分析，取该结构的对称中心为原点，A-A轴对应1榀与6榀，在A-A轴线上原点以左为负值，原点以右为正值，如图6所示.

图6 车辐式索桁架结构平面

3.1 单根上径向索发生松弛分析

由表2和表3可知，实测值索力变化规律与理论、修正值变化趋势一致，单根上径向索松弛对结构内力影响较小，索力变化率随着索力松弛程度增大而增大.由图7可知，上径向索发生松弛的位置索力变化率最大，相邻俩榀索力变化率最小，单根上径向索的松弛对下径向索索力影响较小.

表2 SJXS1松弛50%索力变化率

变化率=(荷载态索力-初始态索力)/初始态索力×100%

表3 松弛100%索力变化率

3.2 单根下径向索发生松弛分析

由表4和表5可知，单根下径向索松弛对结构内力影响较小，索力松弛程度与索力变化率成正比.由图8可知，对于下径向索而言，发生松弛的位置索力变化率最大，相邻俩榀索力变化率最小，单根下径向索的松弛对上径向索索力影响较小.

图7 索力变化量与径向索松弛存在位置的关系(松弛50%)

Fig.7 The relation between the variation of cable force and the location of radial cable relaxation.(Slack 50%)

单根径向索发生松弛时，经过结构预应力重分布，引起的索力变化分配到整个结构索系中，因此对结构内力影响较小.

表4 XJXS1松弛50%索力变化率

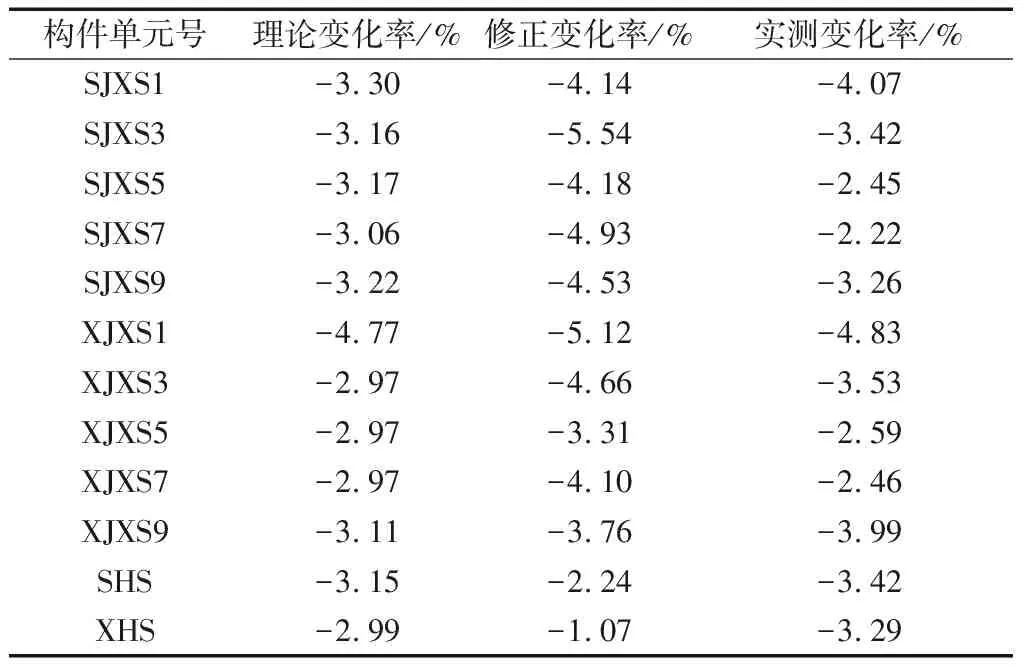
表5 XJXS1松弛100%索力变化率

3.3 单根上环索发生松弛分析

不同松弛程度下的索力增量如图9～图11所示，A-A轴线下节点竖向位移的变化情况如图12所示.由图9～图11可知，实测值索力变化规律与理论、修正值变化趋势一致，索力变化率随松弛程度呈线性变化，上环索松弛对上部索系影响较大，变化率最大为-20%，对下部索系影响较小，变化率最大为-9%，说明上部索系对上环索松弛较为敏感.由图13可知，实测位移略微小于理论位移、修正位移，但变化趋势一致，当上环索发生松弛时，内撑杆下节点位移最大，最大位移为2.3 mm，约为结构跨度的l/3 000.

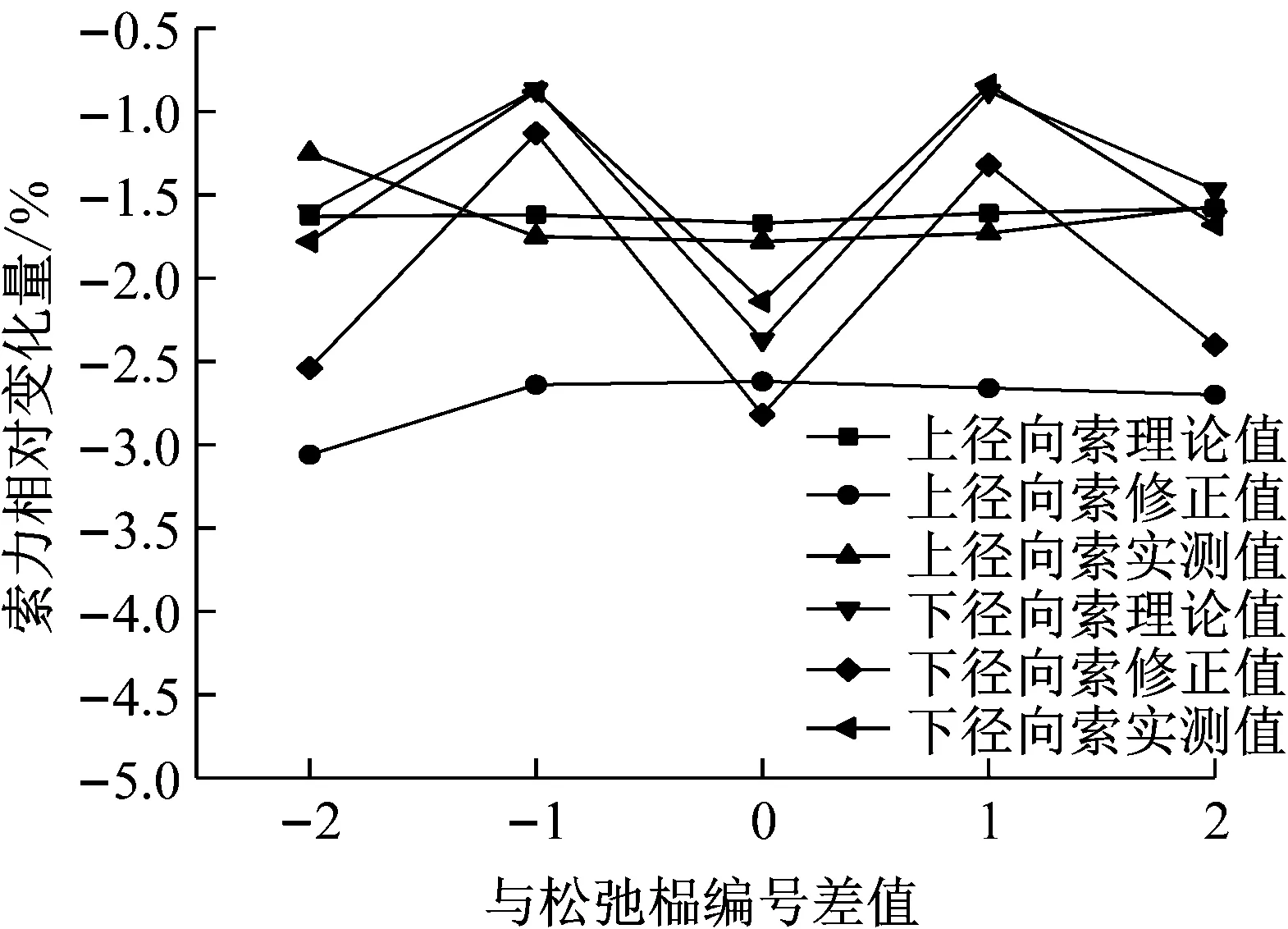
图8 索力变化量与径向索松弛存在位置的关系XJXS1(松弛50%)

Fig.8 The relation between the variation of cable force and the location of radial cable relaxation XJXS1(Slack 50%)

图9 SHS理论索力变化率

图10 修正索力变化率SHS

图11 SHS实测索力变化率

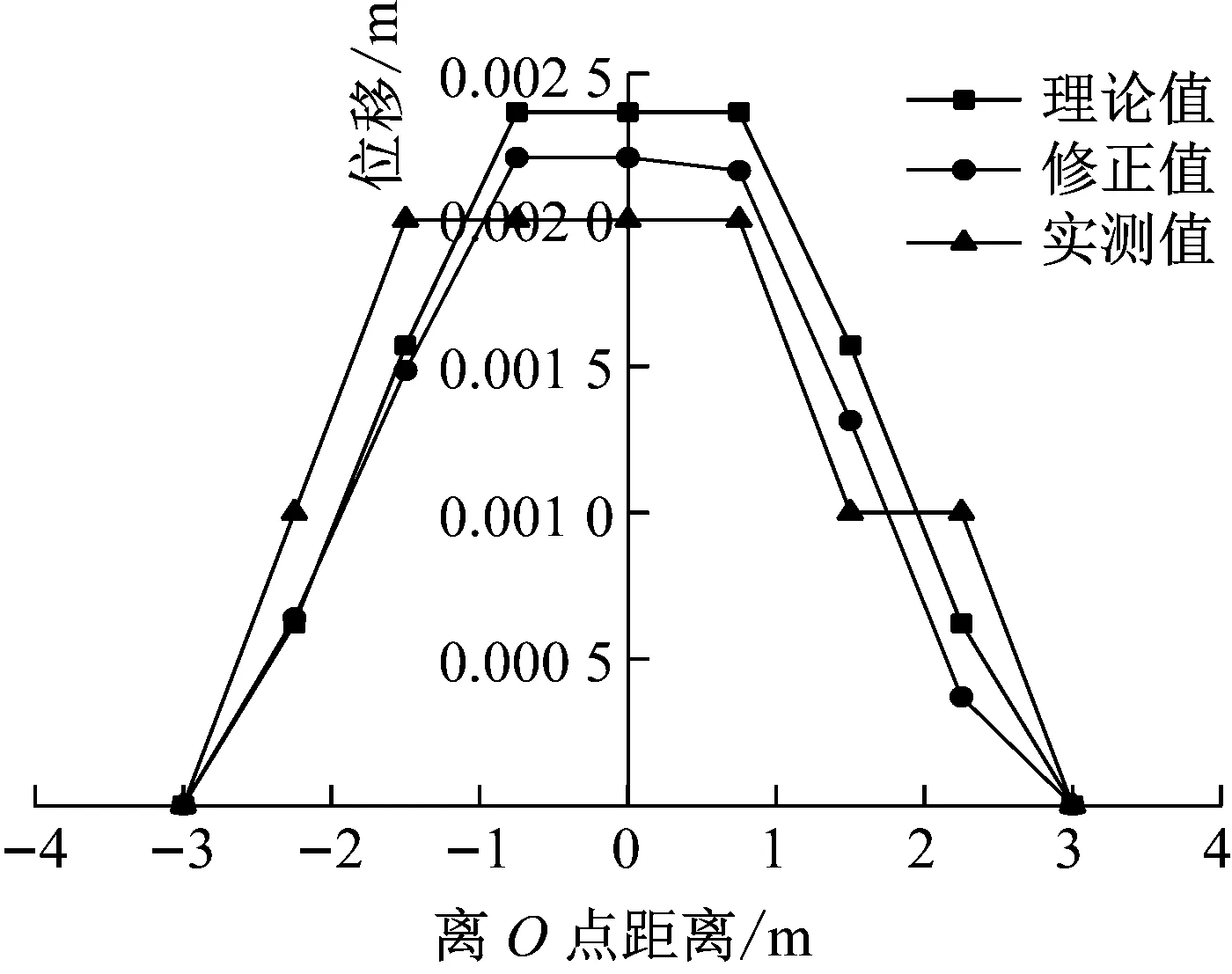
图12 SHS松弛60%撑杆下节点位移

3.4 单根下环索发生松弛分析

由图13～图15可知，上径向索、下径向索、上环索、下环索索力增量基本一致，实测索力增量最大为-9%，说明下环索发生松弛时结构索系敏感性基本相同.由图16可知，当下环索发生松弛时，内撑杆下节点位移最大，最大位移为-2.5 mm，约为结构跨度的l/2 400.

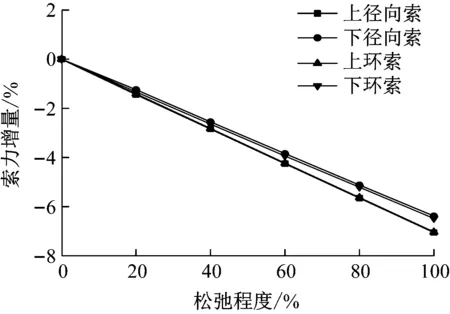
图13 XHS理论索力变化率

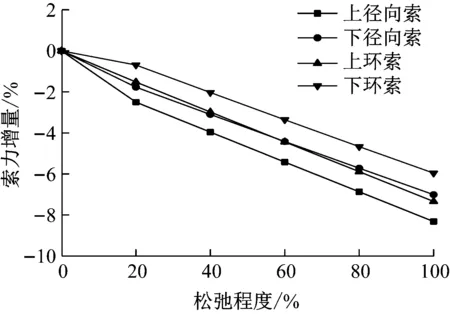
图14 XHS修正索力变化率

图15 实测索力变化率

图16 XHS松弛60%撑杆下节点位移

3.5 全部上径向索发生松弛分析

由图17～图19可知，实测索力增量略大于理论、修正索力增量，全部上径向索松弛对上径向索和上环索影响很大，变化率最大为-59%，对下径向索和下环索影响较大，变化率最大为-27%.由图20可知，当全部上径向索发生松弛时，内撑杆下节点位移最大，最大位移为7 mm，约为结构跨度的l/850.

3.6 全部下径向索发生松弛分析

由图21～图23可知，全部下径向索松弛对上径向索和上环索影响很大，变化率最大为-35%，对下径向索和下环索影响较大，变化率最大为-25%.由图24可知，当全部下径向索发生松弛时，内撑杆下节点位移最大，最大位移为-11 mm，约为结构跨度的l/600.

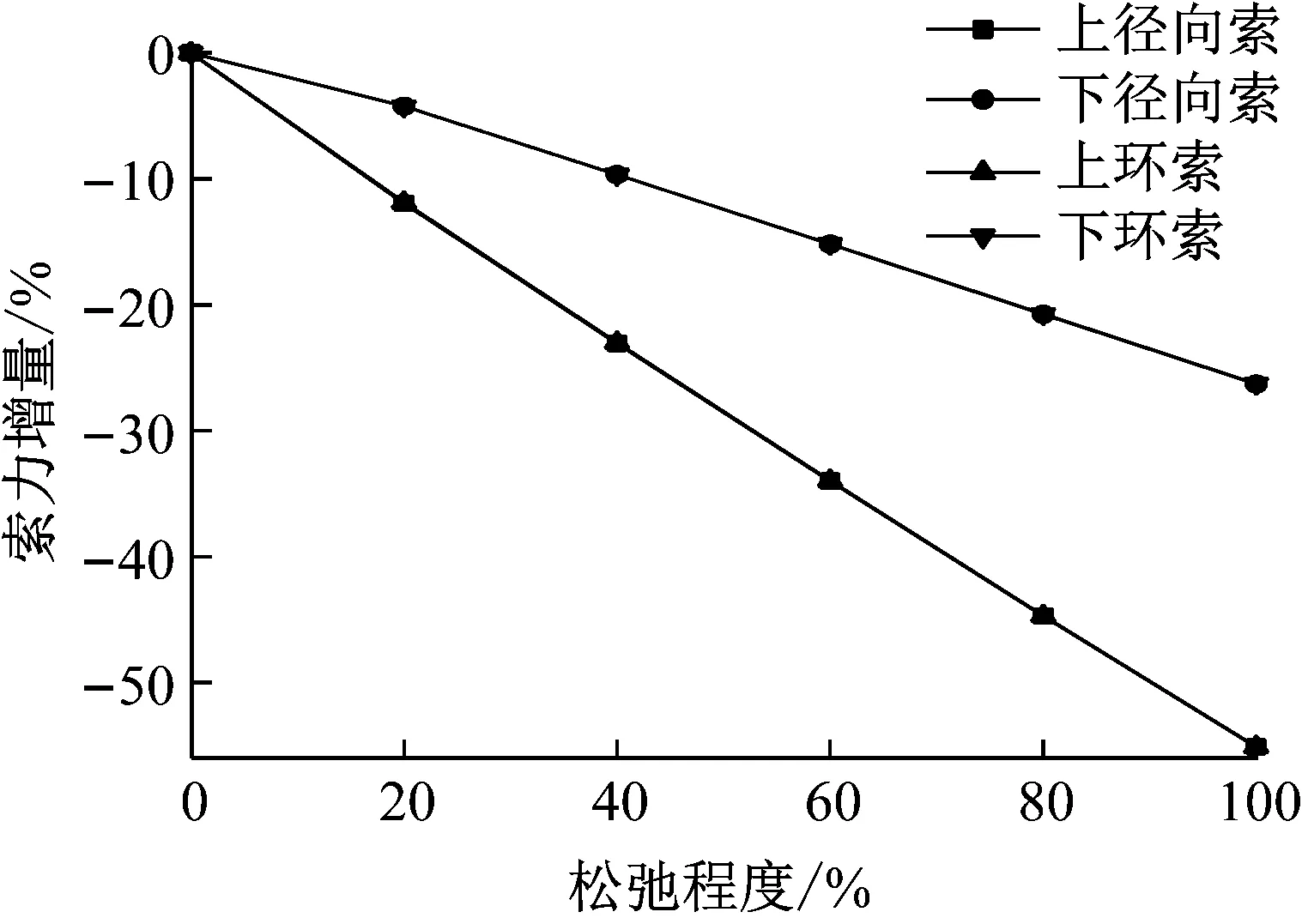
图17 SJXS理论索力变化率

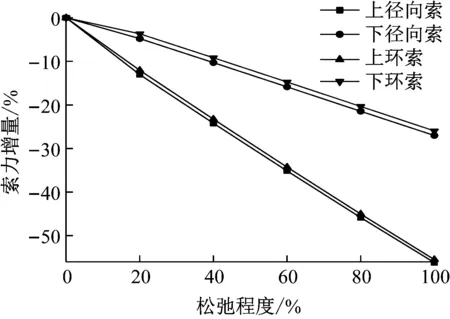
图18 SJXS修正索力变化率

图19 SJXS实测索力变化率

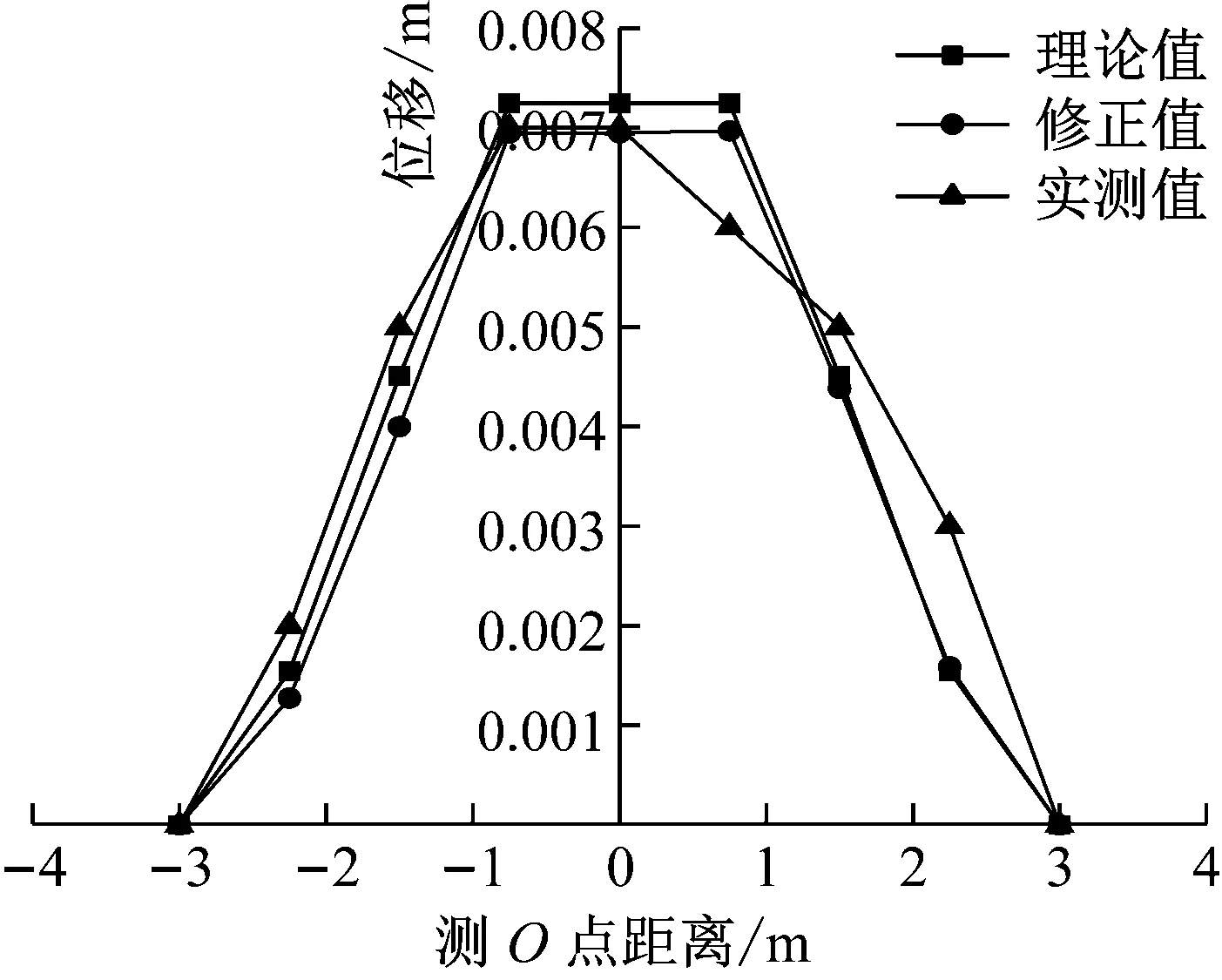
图20 SJXS松弛60%撑杆下节点位移

图21 XJXS理论索力变化率

图22 XJXS修正索力变化率

图23 XJXS实测索力变化率

从拉索松弛索力变化可得出，当结构中单根索发生松弛时，环索松弛对结构力学性能影响最大，定义环索为车辐式索桁架结构敏感性构件；上径向索和上环索为稳定索，下径向索和下环索为承重索，稳定索变化趋势一致，承重索变化趋势一致；当稳定索发生松弛时，稳定索产生的索力偏差远远大于承重索的索力偏差，承重索发生松弛时，稳定索与承重索索力偏差变化基本一致；全部下径向索发生松弛对结构内力最为不利，其次是全部上径向索松弛，为避免结构在服役期间径向索松弛过大导致结构失效，可在车辐式索桁架施工张拉阶段对径向索初始预应力适当补偿.依据拉索不同松弛程度下节点位移变化情况可得出，拉索松弛时，内撑杆节点位移最大，内撑杆节点位移对拉索松弛最敏感；单根索发生松弛时，结构竖向变形较小，全部径向索发生松弛时，结构竖向变形较大，最大可达结构跨度的l/600，结构在较大变形情况下容易出现索膜破裂导致结构失效，上述对径向索初始预应力适当补偿措施也能够缓解结构变形较大问题.

图24 XJXS松弛60%撑杆下节点位移

4 拉索松弛可靠性分析

通过抽样方法拟合结构的响应面，继而用响应面方程代替结构有限元模型，之后采用蒙特卡罗方法对车辐式索桁架结构在正常使用极限状态下进行可靠性分析.分析流程如图25所示.

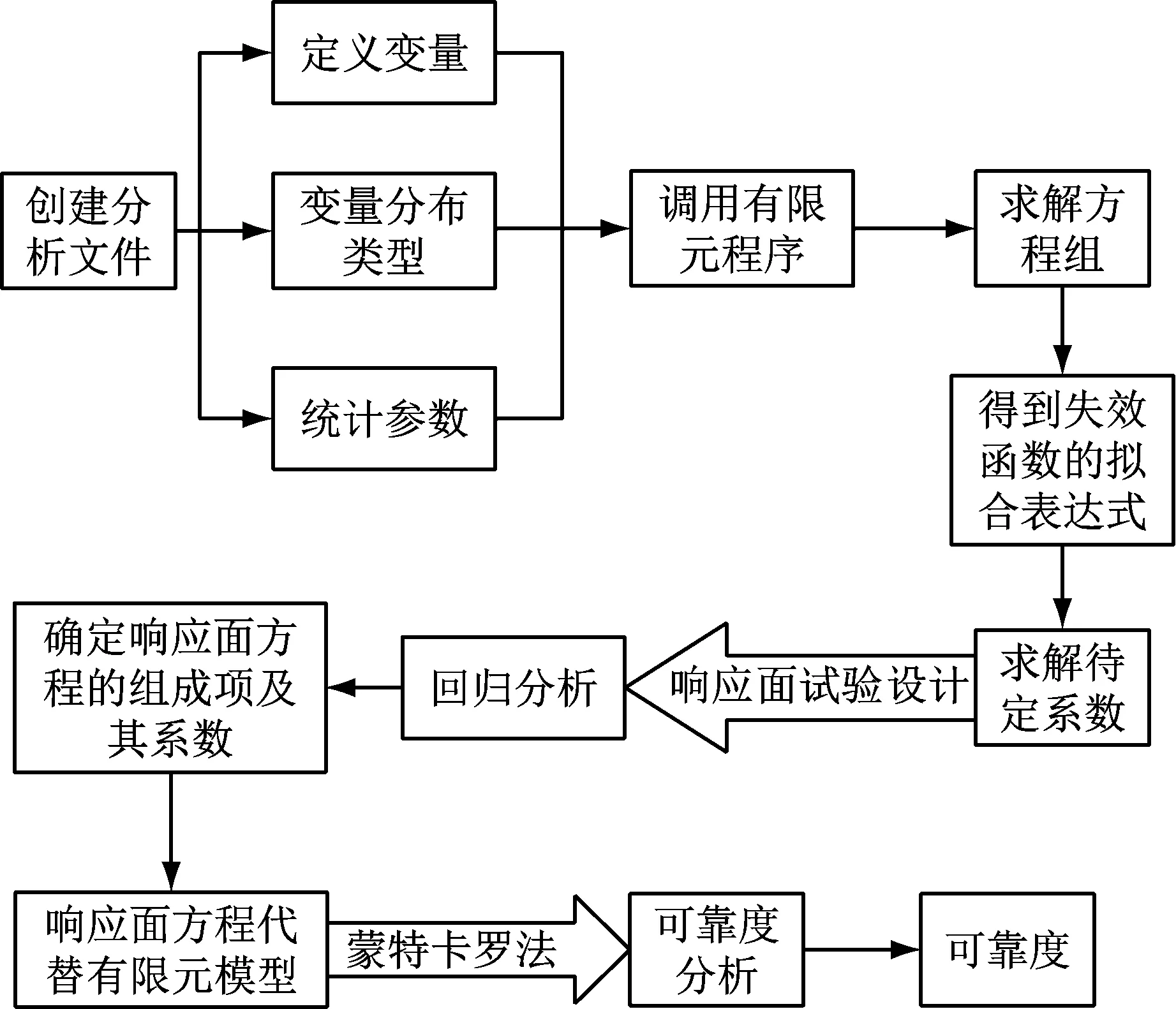
图25 可靠性分析流程

4.1 可靠度分析

假设材料均为理想弹塑性，荷载工况取1.0恒荷载+1.0活荷载，计算时分别考虑各种索长度误差进行分析.

对于车辐式索桁架结构的整体变形失效模式，构造功能函数如下：

g=[u]=-umax

(1)

式中：umax为结构中竖向位移绝对值的最大值；[u]为规定的位移变形限值；L/300为规范规定的位移变形限值.为研究不同位移限值条件下结构可靠度的变化，本文[u]分别取L/350、L/300、L/250，其中L为车辐式索桁架跨度.运用响应面法得到响应方程后，结合拉丁超立方抽样(LHS)执行100万次抽样模拟，得到结构的失效概率.

随机输入参数即车辐式索桁架结构有限元模型中的不确定影响因素.根据结构有限元模型的具体特点和计算需求，输出参数为结构荷载之后的响应参数，通过ANSYS软件计算可以得到输入参数对于输出参数的影响程度—灵敏度，根据定义输出参数的失效判别公式，得到结构的失效概率，进而求出结构的可靠指标.其中定义的随机输入变量和输出变量如表6、表7所示.

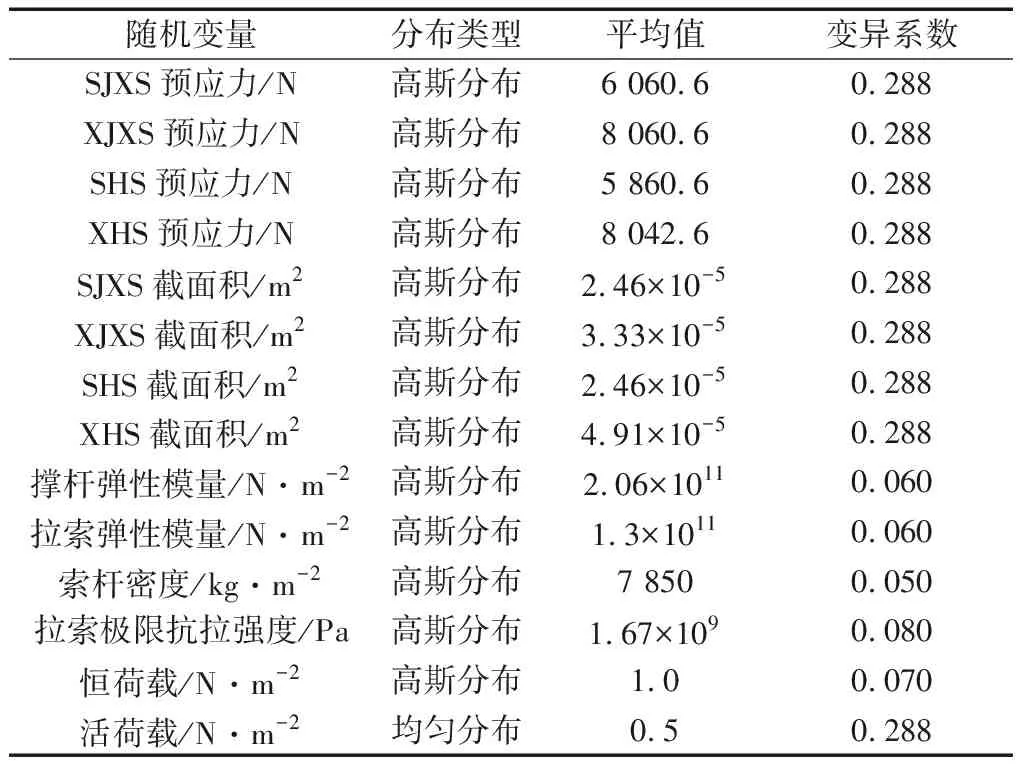
表6 定义随机输入变量

表7 不同标准下的最大位移输出变量

由单根索发生松弛静力分析可知，单根径向索松弛对结构位移影响最小，对结构可靠度影响较小，所以可靠性分析仅提取发生全部径向索发生松弛、环索发生松弛时的结构各输出变量的失效概率，通过Matlab标准正态分布计算进行计算分析，得到不同标准下位移的可靠指标.研究拉索松弛对结构可靠性的影响，由《建筑结构可靠度设计统一标准》可知，结构构件在正常使用极限状态的可靠指标，根据其可逆程度宜取0～1.5，其正常使用极限状态下的可靠指标取选择0.

提取发生松弛时的结构各输出变量的失效概率，得到不同标准下位移的可靠指标，如图26～图29所示.由图26可知，在上径向索预应力松弛至60%前，上径向索随着松弛程度越大，在下径向索张力下结构出现起拱现象，结构可靠指标增大，可适当提高结构变形控制下的安全性，但当松弛程度达到60%以后，上径向索松弛程度较大，结构拉索预应力无法支撑下压荷载，结构位移会突然下降，导致可靠指标突然下降.

图26 全部上径向索预应力损失可靠指标

DMAX1位移限值下松弛程度-可靠度指标拟合方程为

(2)

DMAX2位移限值下松弛程度-可靠度指标拟合方程为

(3)

DMAX3位移限值下松弛程度-可靠度指标拟合方程为

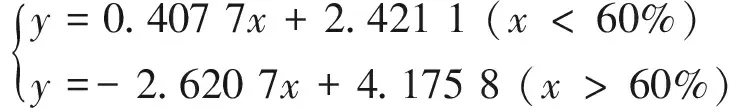
(4)

式中：y为可靠度指标；x为预应力松弛程度.

由图27可知，结构可靠指标随着全部下径向索松弛程度线性降低，结构安全性越低.随着位移限值逐渐增大，可靠度指标增加，结构更加可靠.从整体来看，下径向索松弛对于最大位移可靠指标影响程度较高，在DMAX2位移限值条件下，松弛程度达到70%时，结构可靠度为0，结构失效.在DMAX3位移限值条件下，松弛程度达到42%时，结构可靠度为0，结构失效.

图27 全部下径向索预应力损失可靠指标

DMAX1位移限值下松弛程度-可靠度指标拟合方程为

y=-2.461 8x+1.106

(5)

DMAX2位移限值下松弛程度-可靠度指标拟合方程为

y=-2.411 4x+1.686 6

(6)

DMAX3位移限值下松弛程度-可靠度指标拟合方程为

y=-2.980 6x+2.899 8

(7)

式中：y为可靠度.

由图28可知，结构可靠指标随着上环索松弛程度线性升高，结构更加可靠.当上环索发生松弛时，随着位移限值逐渐增大，可靠度指标增加，结构更加可靠，且在不同位移限值条件下，可靠指标都大于0，可靠度符合相关规范的要求.

图28 上环索预应力损失可靠指标

DMAX1位移限值下松弛程度-可靠度指标拟合方程为

y=0.414x+0.952 5

(8)

DMAX2位移限值下松弛程度-可靠度指标拟合方程为

y=0.377 5x+1.561 2

(9)

DMAX3位移限值下松弛程度-可靠度指标拟合方程为：

y=0.403 7x+2.450 6

(10)

式中：y为可靠度指标；x为预应力松弛程度.

由图29可知，结构可靠指标随着下环索松弛程度线性降低，结构安全性越低，但变化较为平缓，下环索松弛对结构可靠度影响较小，在不同位移限值条件下，可靠指标都大于0，可靠度符合相关规范的要求.

图29 下环索预应力损失可靠指标

DMAX1位移限值下松弛程度-可靠度指标拟合方程为

y=-0.436 5x+1.008 1

(11)

DMAX2位移限值下松弛程度-可靠度指标拟合方程为

y=-0.494x+1.625

(12)

DMAX3位移限值下松弛程度-可靠度指标拟合方程为

y=-0.546 9x+2.547 8

(13)

式中：y为可靠度指标；x为预应力松弛程度.

4.2 灵敏度分析

输出参数为结构荷载之后的响应参数.确定输出参数后，通过有限元模拟计算可以得到输入参数对于输出参数的影响程度，即灵敏度.模拟发生拉索松弛时，随机输入变量对输出变量—结构最大位移(DMAX2)的灵敏性分析，提取具体的灵敏度数值.

分析得到不同索松弛下输入变量灵敏度基本相同，因此只列出上径向索松弛时的灵敏度，分析取位移限值为l/300时，对各随机输入变量与输出变量之间的线性相关系数进行整理，得出各个影响因素的灵敏度，如表5所示.由表5可知，对于发生预应力损失，随机输入变量中下径向索施加的预应力(PREJ1)和活荷载(D2)对位移限值的灵敏度最大，且灵敏度系数随着温度变化不明显.其次灵敏度较大的为下环索施加的预应力(PREH2)和恒荷载(D1).

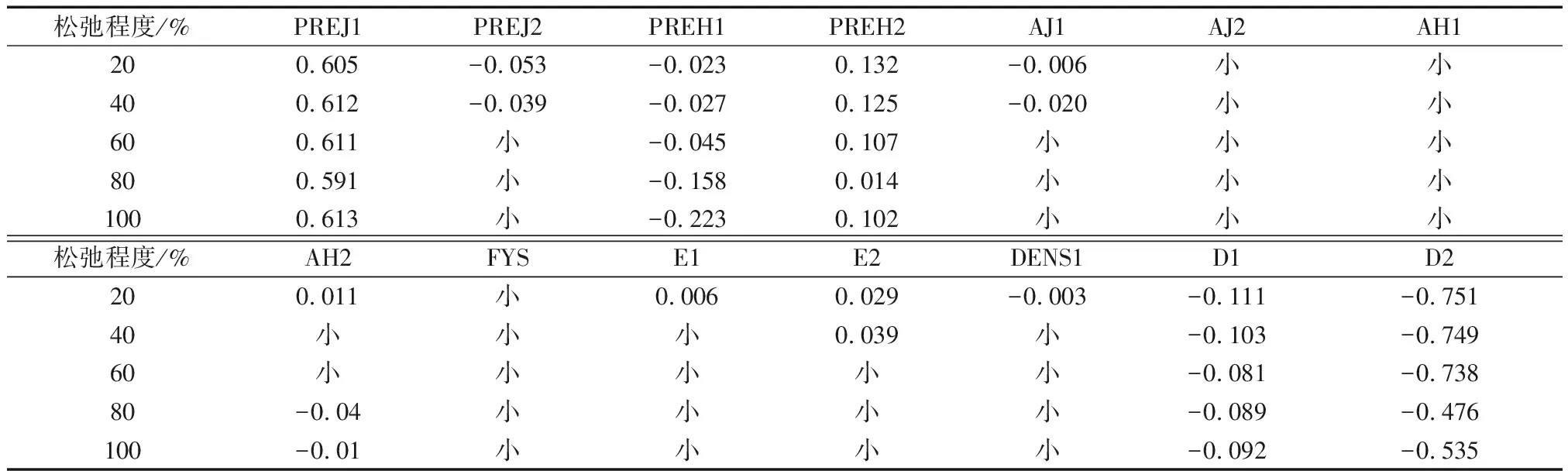
表5 拉索松弛下随机输入变量的灵敏度

4.3 可靠性分析验证

为验证可靠性分析的准确性，将缩尺模型与原实际工程有限元模型(跨度60 m)进行可靠性分析，验证缩尺模型可靠性分析所得到的拟合方程和不同因素的灵敏度.

(1) 可靠度验证

单根索发生松弛的可靠度验证以下环索发生松弛为例，对实际模型进行可靠性分析，得到实际模型下环索发生松弛的最大位移限值l/300可靠度，并将其与缩尺模型可靠度进行对比，如图30、表12所示.

图30 可靠指标对比

表6 可靠指标误差

Tab.6 Reliability index error

预应力损失/%缩尺模型可靠度扩大模型可靠度误差/%200.9240.952 33.1400.846 40.872 13.0600.738 40.755 32.3800.622 90.648 24.11000.599 30.624 54.2

由图30可知，两模型随预应力损失变化的可靠指标变化趋势一致，且由表12可知，缩尺模型与实际模型可靠度相差较小，最大误差为4.2%，因此对缩尺模型进行可靠性分析得到的拟合方程可为实际工程拉索松弛时的可靠度做参考.

(2) 灵敏度验证

对实际模型在下环索松弛60%下进行灵敏度分析，得到实际模型最大位移限值l/300时的灵敏度，并将其与缩尺模型灵敏度进行对比，如图31所示.

a 缩尺模型灵敏度

b 实际模型灵敏度

由图31可知，在下环索松弛60%时，两种模型影响位移限值变量的因素基本相同，影响较大的为下径向索施加的预应力(PREJ1)和活荷载(D2).

5 结论

通过对车辐式索桁架模型试验，研究了拉索松弛对结构的影响，并对其可靠性能进行分析，可以得出以下结论：

(1) 在结构单根索发生松弛时，索杆对结构内力影响程度依次为：下环索>上环索>下径向索>上径向索；全部上径向索发生松弛对结构内力最为不利，可在车辐式索桁架施工张拉阶段对径向索初始预应力适当补偿来减小拉索松弛对结构的影响；在不同拉索松弛程度达60%时，全部下径向索发生松弛时下节点竖向位移最大.一榀索桁架上内撑杆节点竖向位移变化最大，内撑杆节点位移对拉索松弛最敏感.

(2) 可靠性分析方面，当全部上径向索松弛程度达到60%后，结构竖向位移发生突变，可靠指标突然下降，在结构服役期间监测拉索预应力时，在上径向索松弛程度较大(接近松弛程度60%)时，应及时对上径向索进行预应力补偿，防止结构发生突变；上环索预应力松弛对结构可靠度影响较小；对于下径向索和下环索，结构可靠指标随着松弛程度增大线性降低；全部下径向索发生松弛，预应力损失较大时可靠度指标变为负值，结构失效.

(3) 从各结构参数的灵敏度来看，下径索施加的预应力和活荷载的线性相关系数最大，下径向索施加的预应力对可靠度影响呈正相关，适当提高下径向索初始预应力可提高结构安全性能，活荷载对可靠度影响呈负相关，在结构进行维修时，应注意减少活荷载对其影响，导致结构安全性能下降较多.