混凝土扭转剪切徐变试验方法及其应用
2019-08-06牛艳伟曹宏恩汤颖颖
牛艳伟, 曹宏恩, 汤颖颖, 王 涛
(1. 长安大学 公路学院, 陕西 西安 710064; 2. 中国葛洲坝集团 PPP事业部, 湖北 武汉 430033;3. 长安大学 理学院, 陕西 西安 710064)
混凝土的徐变是指在恒定外荷载作用下,结构除产生弹性应变外,其应变随时间继续增大的现象,混凝土徐变是导致混凝土桥梁结构长期变形的主要因素[1-2],对于大跨径混凝土梁桥,徐变效应的控制不当或预测不准将引起变形过大及开裂问题[3].通常梁式桥梁的挠度计算以弯曲应变为主,是否考虑剪切变形根据高跨比决定.已有学者通过抗剪试验研究发现,箱梁开裂后的剪切变形对结构的总体变形影响较大,且随时间推移,影响将不断增加[4-5].并有学者通过分析剪切变形对箱梁挠度的影响规律,推算了箱梁的剪切徐变挠度,并通过计算表明剪切徐变是造成箱梁持续下挠的原因之一[6].随着有限元程序的发展,黄海东等利用ADINA软件开发了空间应力状态下的徐变分析计算子程序[7],汪剑[8]等按照叠加原理进行徐变系数的计算,考虑了温度、湿度及构件局部理论厚度对徐变的影响.文献[9]基于叠加原理实现了ANSYS的混凝土三维有限元徐变计算.上述研究均假设剪切徐变模型与轴向徐变相同.
目前混凝土徐变模型基本上是建立在试验数据基础上的经验公式,2007年Rajeev所对比的多种徐变预测模型[10]以及2014年Wendner提出的B4徐变模型[11],虽然考虑的计算参数和影响因素更加全面,但其试验条件均为单轴应力状态,针对混凝土在剪切应力状态下的徐变试验研究匮乏.轴向受压徐变通常采用文献[12]所提出的凝固理论描述,在此基础上,后续研究提出了三维徐变的微观力学模型[13],增加了对有侧向约束轴压徐变的描述.伴随徐变研究的深入,关于受拉状态下的徐变研究逐渐开展,Hilaire根据受压区和受拉区测点长期应力观测,发现两种受力状态下混凝土的徐变存在较大差异,截面长期应力变化呈现非线性[14].Wei等的研究同样表明现有徐变模型难以对收缩及约束引起的拉应力做出合理预测评估,从而提出了一种优化的受拉徐变模型用以评估拉应力的发展及开裂预测[15].文献[16]开展了裂缝对剪切变形的短期效应的试验研究,但未考虑长期徐变变形.
可见,大跨径混凝土梁桥的剪切徐变影响不容忽视,但由于相关试验研究缺乏,现有的徐变模型还未涉及剪切应力的徐变,难以考虑其影响.由此,本文探讨一种测试混凝土剪切徐变的方法,通过施加扭矩使混凝土构件处于扭转剪切状态,对比轴压徐变计算模型,修正剪切徐变参数,可为混凝土桥梁长期变形的计算和预测提供参考.
1 剪切徐变试验装置及原理
1.1 混凝土剪切徐变试验装置
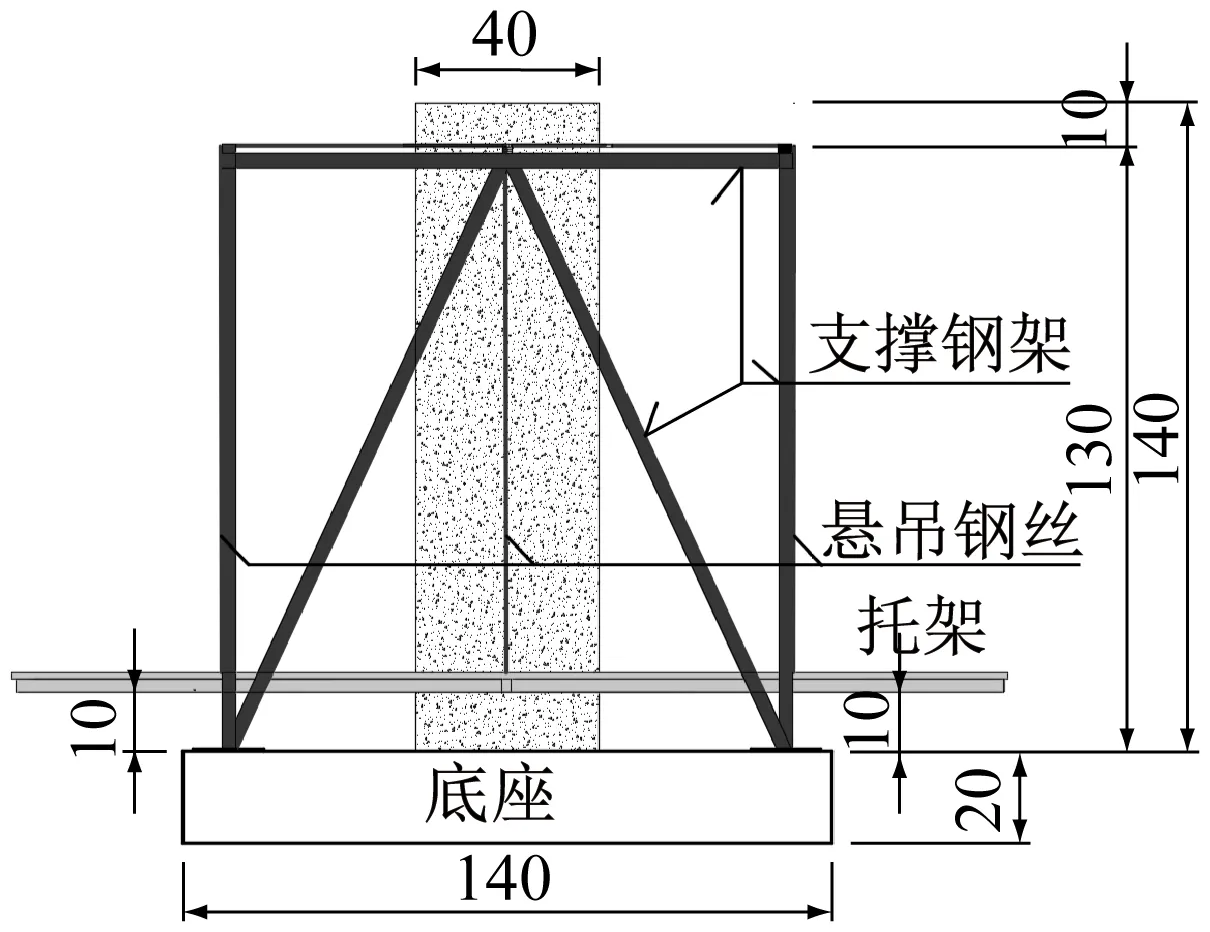
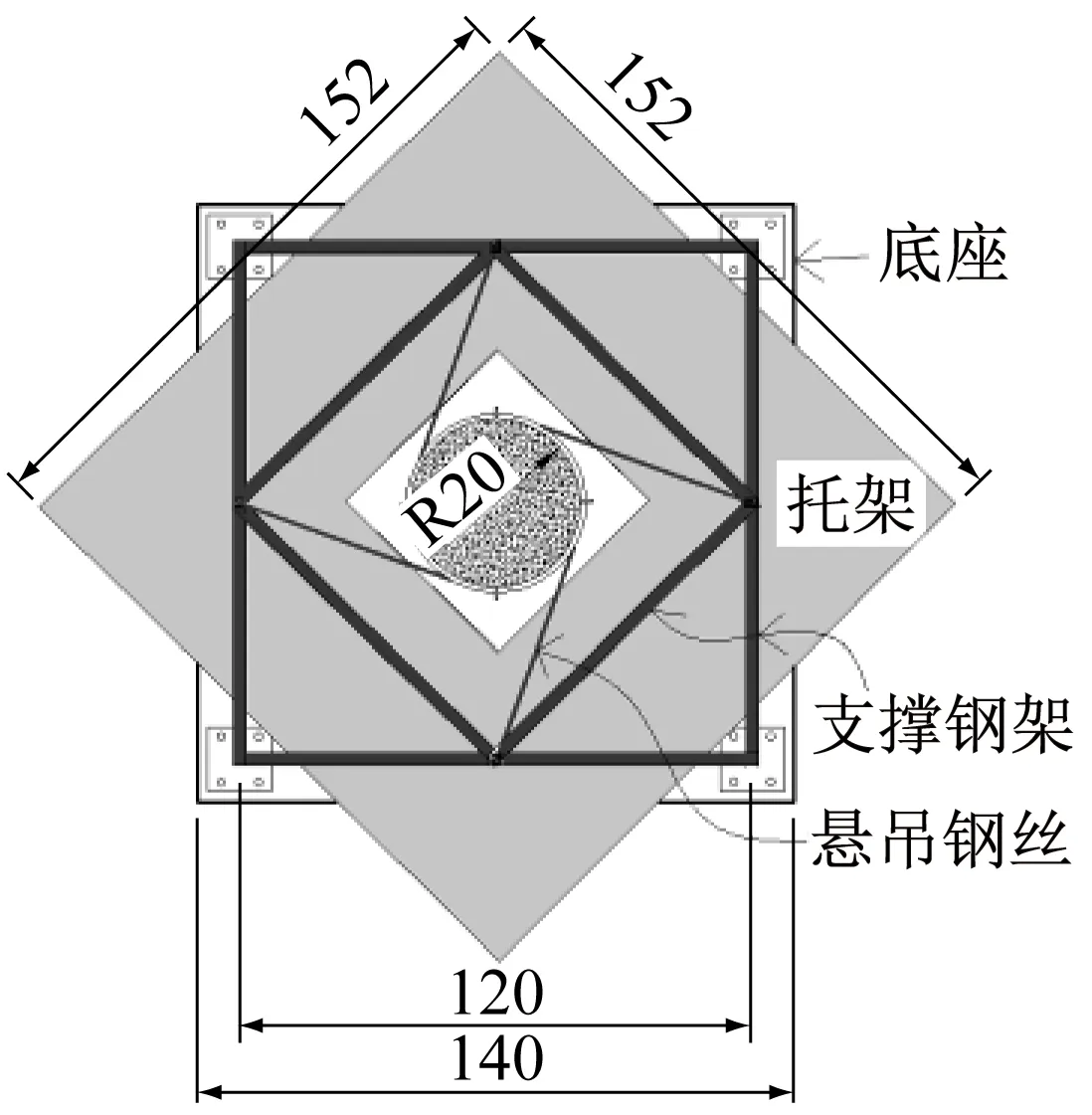
为得到剪切应力作用下混凝土徐变特性,通过对混凝土圆柱体自由施加恒定扭矩,使构件截面只受剪切应力作用.剪切徐变试验装置如图1a所示由三部分组成:① 底座与支撑钢架;② 圆柱体剪切试件;③ 荷载托架与连接的悬吊钢丝.
剪切试件与混凝土底座固结,支撑钢架通过螺栓与混凝土底座固结;荷载托架连接钢丝绳并通过支撑钢架上的转换槽转至水平方向后与试件顶部预埋的传力钢筋连接.共设置4根钢丝绳连接荷载托架与试件,调整钢丝绳长度使悬吊的荷载托架保持水平.加载时将预制的标准荷载块对称、逐步加载到荷载托架上.如图1b所示,托架荷载F由4根钢丝绳通过转换槽将竖向力转换成水平力对称施加到混凝土试件顶部周围,形成扭矩T作用,图中r为试件截面半径.
由于试件在加载后所产生的扭转变形将转换为荷载托架的竖向变形,如图2a所示在荷载托架与底座之间预留10 cm间隙.荷载托架利用支撑钢架与剪切试件之间的空间进行设置,如图2b装置俯视图所示,在托架上堆载后,托架在竖向变位时与支撑钢架和剪切试件均不接触.

a 试验装置构造

b 试验装置传力路径
组装完成的剪切徐变装置如图2c所示,加载时通过调整托架上的标准重块数量,可实现不同应力等级的加载.加载后,底座、试件及荷载托架处于自平衡状态,使试验装置在长期加载过程中保持荷载恒定与体系稳定.
为减小试验构件的尺寸并放大变形以提高测试精度,在测试截面设置定位钢筋并延伸一定长度,测试截面定位钢筋沿切向的直线位移,根据等直圆杆扭转的几何关系,得到构件横截面上的剪切应变.
1.2 混凝土剪切徐变系数测试原理
假定:试件在加载阶段处于弹性范围内,长期测试阶段在线性徐变范围内,试件应力在材料强度的40%以内,不计非线性徐变.
由1.1可知,试验中直接测得的是试件顶端由于扭转产生的切向位移,而剪切变形是用剪切角来度量的,二者转换过程如下:对于承受扭矩作用的混凝土圆柱体,其截面上只有剪切应力,构件在扭转时,横截面上任意一点处的切应变γ(ρ)为
(1)
式中:T为作用在横截面的扭矩;IP为横截面的极惯性矩;ρ为任一点距圆心的距离;G为剪切弹性模量.
a 立面图
b 平面图

c 组装完成图
假设圆柱体高L,截面半径为r,定位钢筋测试长度为l,在试件混凝土龄期为t0时开始加载,则定位钢筋测试点产生的瞬时位移增量为Δu(t0),对应的瞬时切应变γ(t0)为
(2)
式中:arctan()表示反正切函数.
假设持续加载到时刻t,混凝土测试截面对应于长期位移Δu(t,t0)的长期剪切应变γL(t,t0)为
(3)
长期剪切应变γL(t,t0)即剪切徐变引起的应变γc(t,t0),由于混凝土收缩和温度变化并不会导致截面转动,测试结果无需补偿.
假设剪切徐变系数用φsc(t,t0)表示,则根据徐变系数的定义有
(4)
进而可得到加载完成后某时刻t的剪切徐变系数及徐变发展曲线.
承受轴向压力的受压构件的徐变系数为徐变应变与弹性应变的比值,具体可参考相关文献[17].
2 剪切徐变试验模型与加载
2.1 试验模型参数
针对一种材料的徐变试验通常需同时进行3组构件试验[18-19],由于试验条件所限,本次试验仅针对C30混凝土,基于上节徐变装置和测试原理,一共制作了5组构件,包括:3组剪切徐变构件,1组轴压徐变对比构件和1组温度收缩补偿构件(补偿轴压徐变);此外,同时浇筑3组立方体强度标准试件.场地布置如图3所示.

图3 试验场地布置 (单位:cm)
试件与底座采用C30混凝土整体浇筑,所用混凝土配比如表1所示,三组立方体试件的28 d抗压强度为29.6,30.3,30.7 MPa,平均值为30.2 MPa.按照规范,剪切应力和轴向压应力的容许值分别取为1.39和13.8 MPa.

表1 试验混凝土配合比(单位:kg·m-3)
试件参数为:① 三组剪切徐变圆柱体试件实测高度均为140 cm、半径r=19.3 cm;底座为150 cm×150 cm×20 cm的棱柱体.试验构件底座采用双筋布设形式,剪切试件在底座和圆柱体交接位置布置竖向钢筋,避免加载时结合部开裂破坏.如图4a所示,在模型制作过程中底座和剪切试件一次浇筑成形,使二者固结.加载及位移测量位置为距圆柱体试件顶部自由端10 cm处的截面,并在加载处布筋.持续荷载利用预制混凝土块的重力施加,尺寸为15 cm×15 cm×30 cm,单块质量为16 kg,加载完成后的装置如图4b所示.② 轴压徐变试验多采用棱柱体试件[18-19],为与圆柱体剪切试件保持一致,本文的轴压徐变亦采用圆柱体试件;同时为减小堆载,截面适当减小:轴压试验构件为尺寸为100 cm×100 cm×30 cm的底座和高140 cm、半径r=10 cm的圆柱体.如图4c所示,利用杠杆原理对试验构件对称施加荷载,可产生8倍于堆载的轴压加载力(杠杆比为2.4 m/0.3 m);为了防止轴压构件加载端局部破坏,在加载端埋置钢板,并通过销轴的方式与加载工字钢梁连接.③ 由于收缩和温度变化不影响剪切试件的截面转动,因此补偿构件仅用于修正轴压徐变构件;由于仅测试温度和收缩应变,补偿构件高度调整为100 cm.

a 底座与试件固结成形

b 剪切徐变试验加载完成

c 轴压试件加载
2.2 试验加载过程
圆截面剪切试件在扭矩作用下,截面剪切应力由圆心沿径向逐渐增大,在截面外缘达到最大值.为更好的描述剪切徐变与试件剪切应力等级的关系,考虑不同应力的面积占比影响,采用按照面积加权平均的方式取截面平均应力代表值τm定义剪切应力等级状态,如下
(5)
式中:T为截面扭矩;Ip为截面极惯性矩;r为截面半径;ρ为任一点到圆心的距离;τmax为截面最大剪切应力.
按式(5)对3组扭转剪切试验进行截面剪切应力状态等级计算,平均应力代表值τm分别为0.209、0.299、0.352 MPa(容许应力1.39 MPa).
轴压试件全截面受压,则截面的应力状态为
(6)
式中:σc为轴向应力;F为构件所受轴向力;A为截面面积.
根据本次试验加载情况,轴压构件的截面应力为4.7 MPa(容许应力13.9 MPa);4组构件的实际应力控制在容许应力的40%以内,处于线性徐变假设范围.为确保构件在弹性状态范围内受力,按照应力水平对A、B、C、D等4组构件进行分级加载.加载过程中的试验值与弹性理论值对比如图5所示,其中图5a、图5b、图5c为剪切试验加载曲线,图3d为轴压试验加载曲线.总体上试验数据与理论值基本吻合,表明加载完成后试件处于弹性状态.
根据加载过程中的应力-应变曲线,在试验加载完成后4组试验构件的初始应变分别为23.1 μrad(剪切应变为弧度1 μrad=1 rad·10-6)、35.2 μrad、42.2 μrad、137 με(轴压).各试验模型的最终加载情况及产生的最大剪切应力τmax如表2所示.
3 剪切徐变试验结果分析
3.1 试验数据采集
对于3组剪切试验模型,分别在定位钢筋端部布设位移计测量切向位移;对于轴压试件,在1/2高度位置表面,布设振弦式传感器和位移计测量;无荷载补偿块在试件表面安装振弦式传感器.为了保证数据的精确性,试验中位移计底座均安装于独立的钢架上,与支撑钢架脱离,避免加载干扰.

图5 试验加载过程应力-应变曲线
Fig.5 Sress-strain relationship during the loading process

表2 试验模型最终加载情况
注:括号内数值为分级加载值
各组试件在加载全部完成,测试值稳定后,认为弹性阶段变形完成;持荷375 d,传感器接机箱,每0.5 h采集一次数据.为考虑温度变化对轴压徐变的影响,同步采集试验室温度变化数据进行修正.
3.2 试验数据分析
在进行混凝土结构徐变特性计算时,利用实测徐变数据进行规范模型的参数修正是目前建议的较为精确的一种方法[20],在具备试验条件时,在一些大型桥梁项目上已有应用[18].目前轴压状态下的混凝土徐变预测模型主要有指数形式和乘积形式两种,具有代表性的模型包括我国新实施的混凝土桥涵设计规范JTG 3362-2018模型[17](延用JTG D62-2004模型)和AASHTO规范模型[21].
依据JTG 3362-2018模型(以下简称JTG 3362模型),轴向受压徐变系数的理论值如下
(7)
式中:φ0为名义徐变系数,与混凝土28 d龄期时的平均立方体抗压强度、混凝土加载龄期、构件理论厚度以及平均相对湿度有关.本文剪切试验构件理论厚度h=193 mm,轴压试验构件理论厚度为h=100 mm,加载龄期t0为14 d,根据名义徐变系数的计算公式,本试验剪切构件φ0计算值为2.80,轴压构件φ0计算值为3.08.t1=1 d,βH是与构件理论厚度和平均相对湿度相关的系数,根据规范给出的计算公式,本试验剪切构件βH计算值为540,轴压构件βH计算值为400.
针对剪切徐变,因为现行规范还没有专门的计算模型,为与轴压徐变模型进行对比,在JTG3362模型的基础上,引入调整系数α1,α2,α3,则式(7)改写为
(8)
式中:α1用于调整徐变终极值,α2、α3用于调整拟合曲线的发展趋势.将式(8)作为拟合函数应用最小二乘法对试验数据进行优化拟合,从而确定各拟合公式中的未知参数.
各剪切试件徐变系数的拟合曲线如图6所示,通过更新参数使规范修正模型与试验数据具有较高的拟合程度,调整后的参数见表2,表中τm为截面平均应力代表值.
结果表明剪切徐变的徐变终极值均超过轴压徐变终极值,其范围在轴压徐变的2.26~2.63倍.导致3组剪切试验终极值存在波动的主要因素有:① 混凝土浇筑质量的差异;② 试验结果的离散性;③ 剪切应力水平差异的影响.
除α1代表徐变终极值的变化外,α2、α3表示徐变发展趋势的变化,3组扭转剪切徐变试验的α2、α3取值相同(见表3,分别为0.1和3.2),表明3组剪切试验徐变系数的发展趋势基本相同.如图7所示,在徐变终极值相同的情况下(假设为1),长期来看剪切徐变模型的发展速率要高于JTG3362模型(轴压模型);但徐变早期(50 d内)剪切徐变趋势小于轴压徐变,后期则逐渐加快.

表3 基于JTG 3362—2018剪切徐变拟合及修正系数
根据式(7)计算轴压徐变系数随时间的发展曲线,如图8所示,JTG3362规范模型初期计算值与轴压(D组)试验值稍有偏离,但徐变后期规范值与试验值吻合较好,徐变终极值偏差约5%,相关系数为0.858.
由4组试验结果对比可知,剪切徐变均大于轴压徐变,影响机理分析如下:徐变产生的过程为混凝空隙宽度随时间逐渐发生变化,宏观表现为构件产生与受力状态相关的徐变变形.如图9所示,构件在土材料在硬化过程中骨料沉降、拌合水的析出以及干缩应力会在混凝土组成材料的界面上形成一些微裂缝或者微小空隙,混凝土在受到外力后这些微小轴压状态微小空隙在轴向压力(单轴受力)的情况下收到压缩趋于闭合;而构件受扭产生的纯剪状态,可等效为双轴受力,在主轴受拉的同时在正交方向受到压应力作用,其状态较单轴受力明显不利,且微小空隙趋于张开,不易收敛,这是剪切徐变发展速率较快且徐变终极值相对较大的主要原因.图7中P为轴向力;σ为压应力;T为构件所受扭矩;τ为扭转产生的剪切应力;σmin和σmax为等效的主拉和主压应力.

a 剪切试件A

b 剪切试件B

c 剪切试件C

图7 徐变发展曲线对比
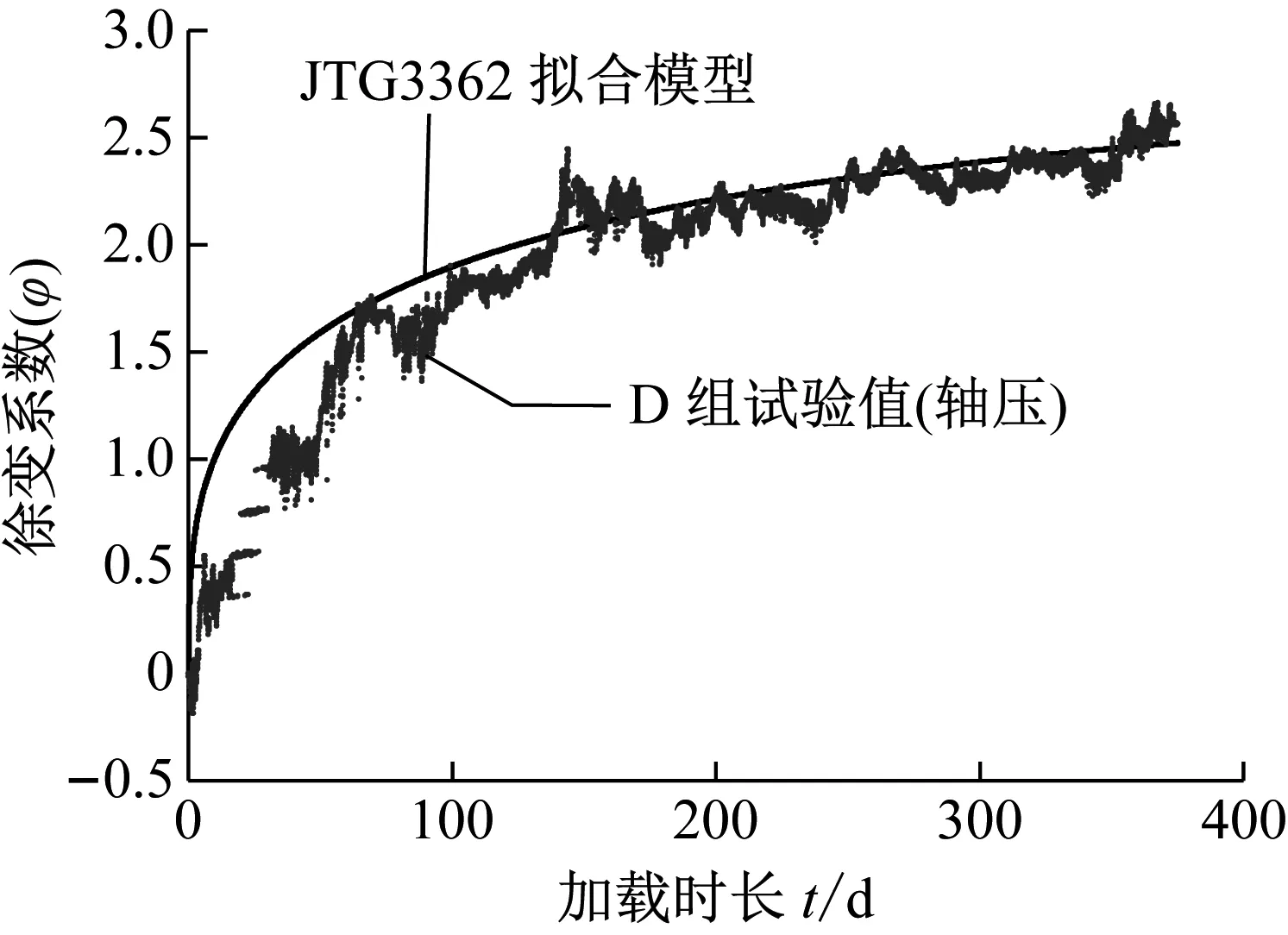
图8 轴压徐变系数(D组)

a 轴压受力 b 剪切受力
4 有限元模拟
剪切徐变系数主要用于需考虑剪切徐变影响的混凝土结构的时变效应计算场合.为验证剪切徐变系数与结构的剪切徐变变形的对应关系和试验方法的有效性,建立三维有限元模型进行模拟.
4.1 计算方法和参数
混凝土三维徐变的计算方法可分为累积增量法和应变率法两种.前者储存每计算时刻的应力增量,可对于应变率法的计算效率较低,但优点是适用性强,适用于所有类型的徐变函数曲线.本文采用累积增量法进行计算,通过改变单元积分点的初应变,计入各计算时刻应变增量对后续计算点徐变变形的影响,具体计算原理见文献[9],不再赘述.
采用通用计算程序ANSYS建立混凝土试验柱的三维有限元模型,如图10a所示,圆柱模型底部固结,柱顶建立刚域并从属于中心节点,在中心节点施加扭矩.模型共计46 080个单元,类型为Solid185,所有单元除径向渐变段外均尽量接近规则六面体,具体离散情况如图8b所示.Solid185单元共含8个积分点,各积分点的应变(S)由6个分量组成,分别为:SX,SY,SZ,SXY,SYZ,SXZ,其中前3项为轴向应变(X方向、Y方向、Z方向),后3项为剪切应变(XY角度、YZ角度、XZ角度).各积分点的徐变应变也由这6项组成,表示如下:f1(SX),f1(SY),f1(SZ),f2(SXY),f2(SYZ),f2(SXZ),其中f1、f2分别为轴向徐变和剪切徐变的计算函数.如设置f2与f1相同,则表示三维徐变采用单一的轴向徐变模型;如设置f2(SXY)、f2(SYZ)、f2(SXZ)均为0值,则表示模型计算不考虑剪切徐变.
有限元模型材料参数与试验模型实测值保持一致,弹性模量为29.2 GPa,泊松比取0.2.模型采用国际单位制(长度单位m,扭矩单位N·m,应力单位Pa)和笛卡尔坐标系,约定如下:坐标原点位于柱底圆心;竖向为Y向;圆柱各横截面位于XZ平面内,以顶部截面为例,如图10b位于X轴的节点13 438的坐标为(X=0.193,Y=1.300,Z=0.在圆心扭矩作用下,同一高度各圆周节点的切向位移均相同,方便起见以下结果均以13 438节点为例.

图10 试验柱有限元模型
Fig.10 Finite element model of test column
4.2 计算结果
如图11所示,圆柱有限元模型在施加扭矩并发生徐变变形后,主要产生围绕顶面圆心的扭转,基本无竖向变形(例如模型C在375 d的竖向变形仅为-4.95×10-16m).这与圆柱承受扭矩处于纯剪切状态,而轴向(竖向)约束扭转正应力几乎可忽略是一致的(竖向应力小于0.007 9 Pa).说明单元各节点的轴向应力很小,模型主要呈现出受剪状态.

图11 扭转剪切徐变变形示意(模型C在375 d时的总变形,放大系数50)
Fig.11 Diagram of tosion shear creep deformation (total deformation of Model C at 375 day, amplification coefficient 50)
以受荷最大的模型C为例,对比4种计算工况:① 仅考虑轴向徐变;② 轴向徐变、剪切徐变相同(均为JTG3362);③ 轴向徐变+试验剪切徐变模型;④ 仅试验剪切徐变模型,不考虑轴向徐变.
如图12所示,对于扭转受力构件,若仅考虑轴向徐变、不考虑剪切徐变,则完全不会产生长期变形,可见对于剪切受力显著的结构,在计算长期变形时必须考虑剪切徐变的影响;若剪切徐变采用与轴向徐变相同的模式(JTG3362),则长期变形计算结果偏小(偏不安全);由于纯扭转的构件的轴向应力可忽略,因此同时考虑轴向徐变和剪切徐变③和仅考虑剪切徐变④的计算结果基本重合.工况③375 d的剪切应变与弹性应变的比值为6.47,与材料的徐变参数6.52相差仅0.77%,从而验证了采用本文方法可有效测试混凝土的剪切徐变系数.
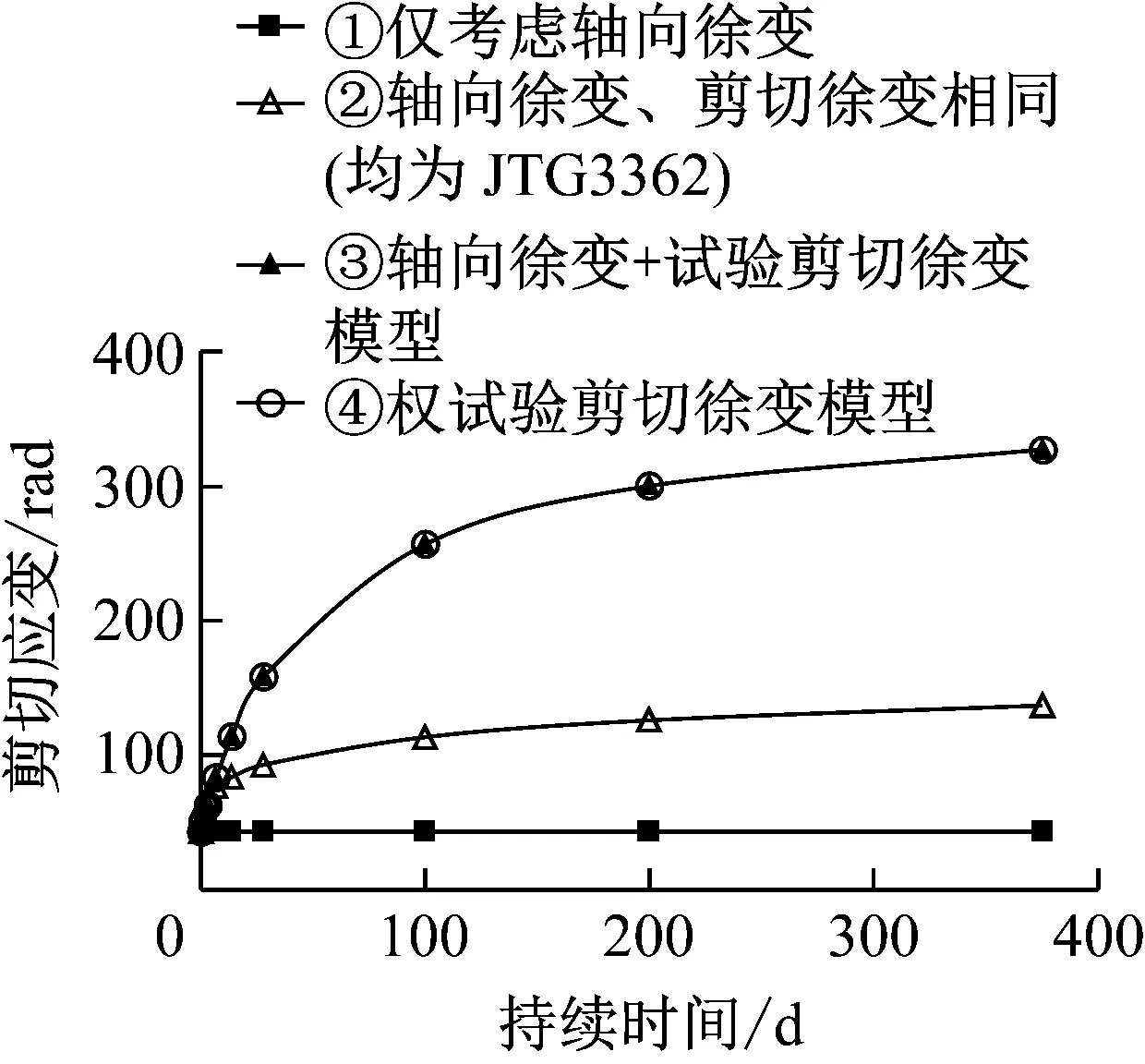
图12 有限元结果对比
5 结论
(1) 针对混凝土剪切徐变系数,提出了基于扭转的试验装置,可用于混凝土剪切应力的分级施加与长期稳定持荷.
(2) 利用扭转剪切推导的徐变系数计算公式,通过切向位移得到徐变系数发展系数,可为试验分析提供参考.
(3) 混凝土剪切徐变试验表明:剪切徐变早期发展小于轴向徐变,后期则逐渐加速;C30剪切徐变值可达规范轴压徐变值的2.31~2.62倍;随着应力的增加,徐变终极值有增长趋势.
(4) 对于受扭构件和其他剪切应力显著的构件,在长期变形计算时应计入剪切徐变系数.基于累积增量法的三维徐变计算程序可考虑剪切徐变与轴向徐变的差异.
(5) 由于试验条件所限,本文只进行了3组构件的试验应用,更加深入的混凝土剪切徐变系数的测定工作,包括考虑混凝土强度等级变化、龄期变化、剪应力增大后的非线性效应等影响和针对性的表达式需进一步开展研究,以期形成较为完整的剪切徐变预测模型.
