梁侧锚固钢板法加固混凝土梁的非线性有限元分析
2019-08-06吴振丽陆洲导李凌志张佳旭
吴振丽, 陆洲导, 李凌志, 张佳旭
(同济大学 土木工程学院, 上海 200092)
对现有建筑功能的多样化需求,导致结构布置改变或者出现超载,从而需对其进行加固处理.对于钢筋混凝土梁而言,常用加固方法有采用混凝土或其他水泥基材料增大截面[1-2]、黏钢[3]或黏碳纤维加固[4-5]等.大量研究表明黏钢和黏碳纤维[3,6-7]能显著提高梁的抗弯承载力和延性,但是在剪应力作用下由于锚固不足容易发生剥离破坏.梁侧锚固钢板法[8](简称BSP法)是通过锚栓将钢板固定在梁侧面从而使其达到加固的技术.Barnes等人[9]对“强弯弱剪”梁分别在其梁侧采用黏钢法和BSP法进行加固,对比发现两者均能显著提高梁承载力,但是黏钢法加固效果低于BSP法,主要原因为黏贴钢板端部锚固不足,在剪应力作用下发生了剥离.
国内外学者对BSP梁的受力性能进行了一系列的研究[10-21],发现由于螺栓的剪切变形,钢板与混凝土间存在纵向和横向相对滑移,其量值由钢板与混凝土梁的刚度比及螺栓的滑移响应决定[14-16].由于相对滑移的存在,BSP梁抗弯刚度降低、延性变大,而受弯承载力基本上保持不变[17-18].而由于BSP梁受剪时,主斜裂缝接近梁端部,钢板端部螺栓数量不足将使螺栓发生较大滑移甚至钢板端锚失效,导致受剪承载力严重降低,甚至受剪破坏模式的转变[19-21],因此在数值分析中必须考虑锚栓滑移效应.
目前对BSP梁受剪性能的研究基本为试验研究,但由于进行试验所需成本较高,且受到试验设备、材料等外界因素的限制,尚未对其受剪性能进行全面参数分析,且实验过程中很难测得钢板和混凝土梁之间的相对滑移.而数值分析作为重要的研究手段,结合试验研究,建立准确的数值模型,能为其提供详细的研究依据.
有限元分析软件OpenSees是由加州大学伯克利分校主导研发的一款开源分析软件.国内外众多学者已基于此软件对混凝土构件进行了力学响应分析.陆新征[22-23]等人开发了分层壳单元,该单元基于复合材料力学原理,将一个壳单元划分为很多层,各层根据需要设置不同的厚度和材料性质,各层材料之间满足平截面假定,且考虑钢筋混凝土面内弯剪共同作用效应和面外弯曲效应.
为了准确全面了解BSP梁的受力性能和变形特性,本文采用OpenSees基于壳单元对BSP梁进行了非线性有限元分析,目的在于:模拟加载条件,采用合理的单元模型和本构关系对BSP梁进行数值模拟,并与试验结果进行对比分析,验证数值模型的准确性;对影响加固梁受剪性能的主要因素进行参数分析,研究其工作机理,得出影响其受剪性能的相关因素及其作用规律,提出BSP法加固的设计建议.
1 试验概况
试验模型[20]为5根钢筋混凝土梁,其中1根为未加固对比试件(Ctrl)另4根采用BSP法进行加固,加固方案见表1,其中Ctrl为参照组.试件截面尺寸、配筋情况、钢板及螺栓的布置方案、加载点布置见图1.试件均采用4点加载,加载时利用千斤顶和分配梁对各点施加集中荷载(F).所有试件均按“强弯弱剪”设计,其混凝土强度等级为C60,纵向钢筋为Ⅲ级热轧钢筋(C),梁侧钢板用高强螺栓与混凝土连接,螺栓直径(D)为12mm,锚固长度取100mm,螺栓水平对称布置.
注:编号中P代表钢板高度; B代表锚栓间距,例如P3B1即代表了加固方案为300 mm高的钢板、100 mm的锚栓间距.
2 有限元分析
2.1 混凝土
本文采用弹塑性有限元分析软件OpenSees对BSP梁进行有限元模拟.混凝土采用分层壳单元模拟,该单元采用的多轴受力混凝土模型基于损伤力学和弥散裂缝模型来模拟混凝土的二维受力行为.弥散裂缝是将开裂的混凝土单元仍然当做一个连续的单元考虑[22],不考虑开裂处的单元离散化,认为裂缝弥散于混凝土单元内.

a 梁加固

b 梁配筋
2.2 钢筋
在分层壳单元中,可以通过“弥散”钢筋模型来考虑钢筋布置.但是由于剪力作用下BSP梁中钢筋受力复杂,为了提供模型准确性,采用“离散”钢筋模型,使用Truss单元来模拟.该单元只考虑轴向力和轴向变形,忽略截面方向几何变形的影响,并赋予由Mengotto与Pinto提出的steel02本构模型[24].
2.3 钢板
由于BSP梁中钢板主要在平面内受力,因此采用平板壳单元进行模拟.该单元是一种高性能四边形平板壳单元,由平面膜单元和板弯曲元耦合而成,能够模拟壳体的复杂受力状态[24].钢材作为各向同性材料且破坏准则符合Von Mises弹塑性模型,因此可以使用OpenSees预设的基于偏二张量的J2 Plasticity Material本构关系来模拟.
2.4 锚栓连接
在实际工作中,BSP梁横向剪切变形和纵向弯曲变形会使锚栓受到横向和纵向两个方向的合力,从而产生滑移,而该锚栓滑移会导致BSP梁受剪承载力严重降低,甚至受剪破坏模式的转变,因此在数值分析中必须考虑锚栓滑移效应.本数值模拟中,引用了零长度单元作为非线性弹簧,赋予其Hysteretic单轴本构模型来近似模拟,并利用矢量加法的原理将赋值的单轴本构分解到横向和纵向两个方向上去,从而可考虑纵横向滑移的综合效应,如图2所示.
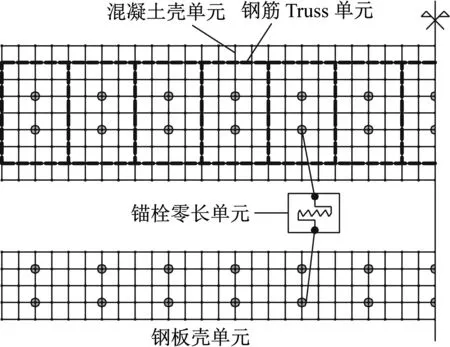
图2 BSP梁单元(一半)
2.5 网格划分、边界、加载及分析设置
混凝土及钢板模型网格沿梁高度、长度均按50 mm划分,如图2所示.
试验中加固梁设置为简支梁,故在建模过程中在支座中心设置约束,一端设置平面内纵向和横向的约束,其余4个方向无约束;另一端仅设置横向约束,其余5个方向无约束.
为了使模型中加载方式尽量与试验加载相同,在荷载定义时需要注意避免出现应力集中,采用多节点等效加载的方式.收敛准则采用了位移控制方式,采用了Krylovnewton算法进行迭代计算.
3 分析结果
3.1 跨中位移-荷载曲线
将上述有限元模型计算所得结果与试验测得的荷载-跨中挠度曲线对比如图3所示,其中FEM表示模拟,TEST表示实验.试件极限荷载(Pu)及跨中位移模拟与试验的对比列于表2.
由图3和表2可看出:试验数据和模拟结果具有良好的一致性,宏观上说明本文建立的有限元模型、选用的材料本构及滑移本构等可以较好地模拟BSP梁的受剪承载力和变形.
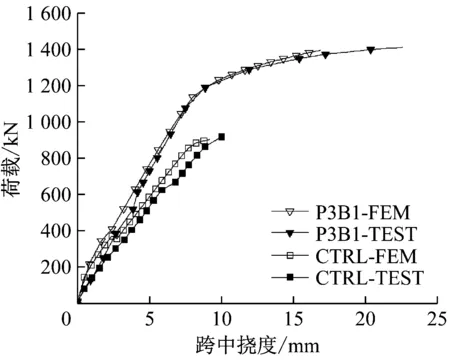
图3 试验结果与模拟结果对比
表2 试验和模拟结果对比
Tab.2Comparison between test results andsimulation results
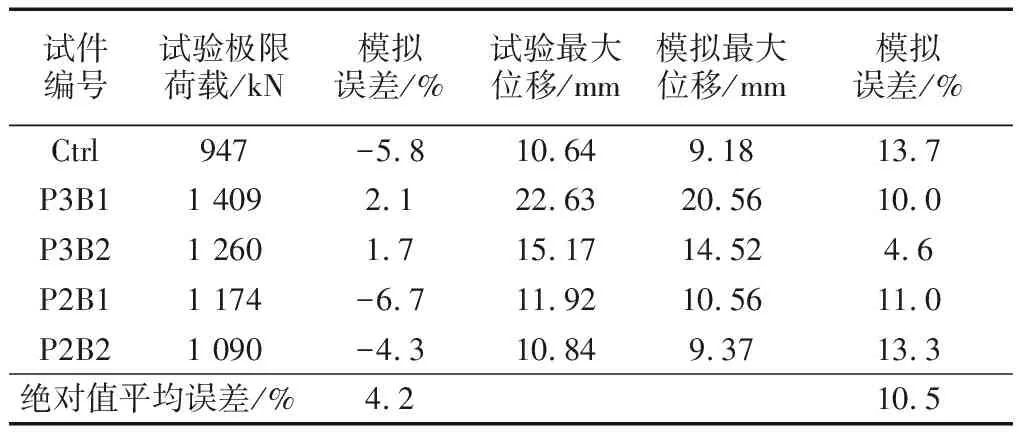
试件编号试验极限荷载/kN模拟误差/%试验最大位移/mm模拟最大位移/mm模拟误差/%Ctrl947-5.810.649.1813.7P3B11 4092.122.6320.5610.0P3B21 2601.715.1714.524.6P2B11 174-6.711.9210.5611.0P2B21 090-4.310.849.3713.3绝对值平均误差/%4.210.5
3.2 钢筋应变对比
图4为数值模拟所得的试件P2B1钢筋应变曲线与试验结果的对比.由于混凝土离散性和数值模型使用的弥散裂缝模型无法准确模拟出实际裂缝情况等客观原因,导致模拟试件结果稍大,但相对误差不大,且没有改变钢筋总体受力趋势,表明该模型能较合理地模拟BSP梁的箍筋和纵筋应变jn.

图4 P2B1梁试验和模拟钢筋应变对比
Fig.4 Strain curves of steel reinforcement in P2B1
3.3 剪跨区钢板应变对比
图5为数值模拟所得的钢板应变(P2B2)与试验结果比较.其钢板上下边缘应变测点Sn和钢板中部主拉压应变测点hn布置如图5a所示.由图5b可知:模拟曲线在加载初期和试验曲线相差极小,当加载到0.7Pu左右时,和试验曲线存在一定误差,主要由于平板壳单元无法模拟钢板平面外屈曲.由图5c可知,钢板中部主压应变在加载初期呈线性增长,模拟曲线与试验曲线基本吻合;当加载到0.4Pu左右,模拟结果与试验结果开始出现离散,模拟结果增长变缓,但是直到加载至Pu,其相对误差仍然很小.可以看出,数值模拟可很好地模拟BSP梁钢板应变变化.

图5 P2B2梁钢板应变曲线对比
Fig.5 Strain curves of steel plate in P2B2
4 参数分析
为了弥补试验中试件数量有限的不足,在验证有限元模型的准确性之后,采用有限元分析对影响BSP梁受剪性能的主要参数进行分析.
4.1 锚栓行数
图6变化的参数是锚栓行数,其中P3B1-n中n表示行数.从图6a中可以看出,在加载初期,曲线斜率没有明显变化,即增加锚栓行数对BSP梁的初始刚度无影响;加载后期,两行锚栓试件比单行锚栓试件有明显的上升,主要由于两行锚栓可以在钢板上传递力偶,但是多行锚栓曲线与两行曲线基本吻合,即加固设计中仅通过增加锚栓行数无法增加试件受剪承载力.
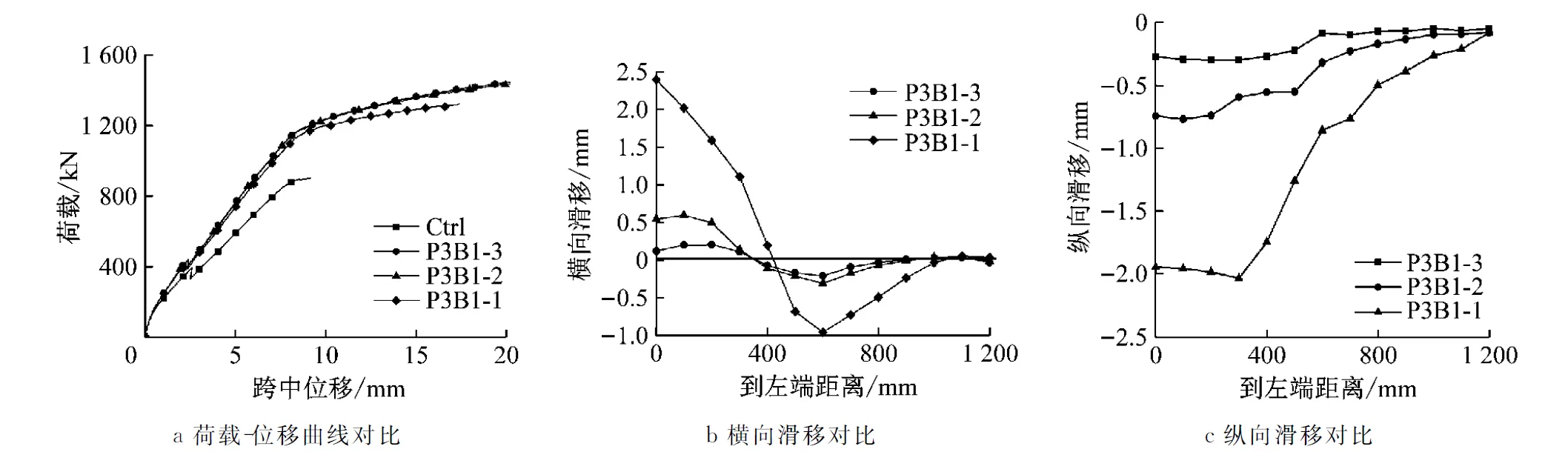
图6 不同锚栓行数变形对比
图6b为垂直于梁轴线的横向滑移,在集中力作用处出现了正向和负向滑移的最大值.图6c为沿梁轴线的纵向滑移,从图中可看出锚栓行数越多,相对纵横向滑移越小.可知增加锚栓行数可有效减小相对滑移,提高BSP梁承载力和延性.
4.2 纵向锚栓间距
图7变化参数为纵向锚栓间距,其中P3Bn中n表示锚栓间距.如图7a所示,四组荷载-位移曲线均表现出明显的弹性阶段和塑性阶段,锚栓间距越小,弹性阶段刚度越大;且BSP梁最大位移和极限荷载也随锚栓间距的减小而增大.对比图7b和7c发现,锚栓间距越小,相对滑移越小,BSP梁承载力越高,延性越好.
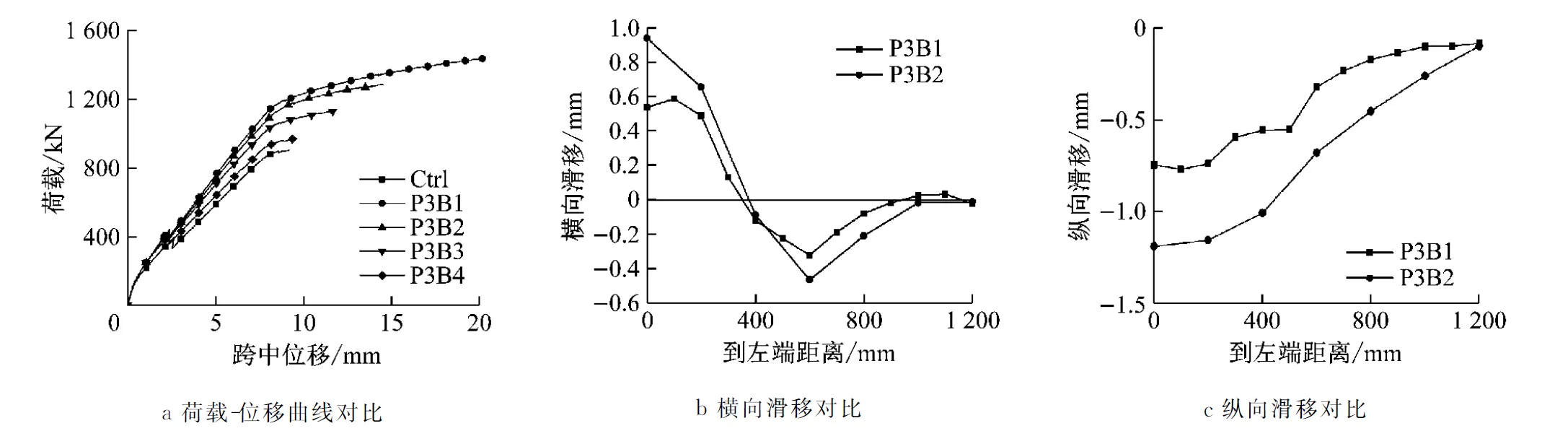
图7 不同纵向锚栓间距
Fig.7 Different anchor bolt spacing along the beam
4.3 钢板高度
图8变化的参数是钢板高度,其中PnB2中n表示钢板高度为n00.从图8a中看出,当钢板高度小于300 mm时,荷载-位移曲线仅有线性增长阶段,此时BSP梁表现出明显的剪切脆性破坏;当钢板高度达到300 mm后,荷载-位移曲线表现出明显的弹性阶段和塑性阶段,钢板高度越大,弹性阶段刚度越大;且BSP梁最大位移也随钢板高度增大而增大.从图8b和8c可看出,钢板高度越大,相对滑移越大,BSP梁承载力越高,延性越好.

图8 不同钢板高度
Fig.8 Different steel plate depth
4.4 钢板厚度
图9变化的参数为钢板厚度,其中P3B2-tn中tn表示厚度为n.从图9a中可看出四组BSP梁的荷载-位移曲线均表现出明显的弹性阶段和塑性阶段,钢板厚度越大,弹性阶段刚度越大;且BSP梁最大位移和极限荷载也随钢板厚度增大而增大.从图9b和9c可知,钢板厚度越大,相对滑移越大,BSP梁受剪承载力越高,延性越好.这与前面讨论的结果不同,这是因为钢板厚度越大,钢板发生相同形变时,钢板承受的荷载越大.

图9 不同钢板厚度
4.5 钢板屈服强度
图10变化的是钢板屈服强度,其中P3B1-Sn中Sn表示屈服强度为n00.从图10a中可看出,四组荷载-位移曲线均表现出明显的弹性阶段和塑性阶段,钢板屈服强度对BSP梁弹性阶段刚度的影响可以忽略不计.当钢板屈服强度从150 MPa增加到400 MPa,BSP梁的受剪承载力有明显提升.但是当其超过400 MPa后,继续增大钢板屈服强度对BSP法加固梁的极限荷载影响极小,可以忽略不计.这主要由于当钢板屈服强度大于一定数值后,梁在加载过程中钢板应力未达到钢板屈服强度就已屈曲,并未发挥钢板全部的受力性能.

图10 不同钢板屈服强度
Fig.10 Different yield strengths of steel plates
由图10b和10c可知,当钢板屈服强度小于400 MPa时,相对纵横向滑移随钢板强度增加而增加;但当钢板屈服强度大于400 MPa后,其对相对滑移、加固梁受剪承载力及延性的影响不大.
4.6 锚栓直径
图11变化参数为锚栓直径,其中P3B2-dn中dn表示直径为n.从图a可以看出,BSP梁荷载-位移曲线均表现出明显的弹性阶段和塑性阶段,当锚栓直径小于16 mm时,随着直径的增大,BSP梁的承载能力和最大位移稍有提高;当锚栓直径增大至16 mm后继续增加,曲线与16 mm时基本吻合.从图11b和11c可以看出,锚栓直径越大,钢板和混凝土的相对滑移越小,钢板与混凝土梁连接越紧密.

图11 不同锚栓直径
Fig.11 Different anchor bolt diameters
4.7 剪跨比
图12变化参数为BSP梁的剪跨比,其中P3B2-n中n表示剪跨比为n.从图a可知,五组荷载-位移曲线均表现出明显的弹性阶段和塑性阶段.随着剪跨比增加,BSP梁的受剪承载力和刚度均减少.从图12b和12c可看出,横向滑移在弯剪区的零点位置、最大值位置与剪跨比有关,即与荷载作用位置有关,具体位置和随荷载作用点位置呈正相关;纵向荷载在弯剪区的变化率也与剪跨比有关,剪跨比越小,变化率越大.

图12 不同剪跨比
Fig.12 Different shear span ratios
4.8 混凝土强度等级
图13变化参数为混凝土强度等级,其中P3B2-n中n表示混凝土强度等级为n.从图13a中可以看出,随着混凝土强度等级增加,BSP梁的初始刚度、最大位移和极限荷载有明显的增加;当混凝土强度低于40 MPa时,荷载位移曲线基本呈直线,呈现明显的脆性破坏;当强度增加至40 MPa后,荷载-位移曲线开始出现塑性阶段,BSP梁的延性和变形能力有显著提高.从图13b和13c中可知,混凝土强度越大,钢板与混凝土之间的相对滑移越大.

图13 不同混凝土强度等级
Fig.13 Different concrete strength grades
5 设计建议
根据上述分析结果可知,影响BSP梁受剪性能的主要因素有:锚栓间距、钢板高度、钢板厚度,而锚栓排数、锚栓直径、钢板屈服强度对加固效果有一定影响.因此,在实际工程应用中,可选钢板屈服强度为400 MPa,锚栓直径为16 mm,且钢板高度不大于300 mm时,可只设置2排螺栓,并在允许范围内减少锚栓间距,增大钢板高度、厚度,以获得较大的受剪承载力、刚度和较好的延性.
6 结论
采用OpenSees软件对BSP梁进行了非线性有限元分析.通过对模拟结果的分析,可得出下列结论:
(1) 有限元模拟结果与试验的宏观、微观数据均保持较高的一致性,说明OpenSees用于模拟BSP梁受剪性能试验具有较高的准确性和可靠性.
(2) 当加强连接件,即增大锚栓排数和直径,减少锚栓间距时,钢板与混凝土间相对滑移减少,增加了BSP梁的整体性,从而提高了受剪承载力和延性;当加强混凝土梁或钢板,即增加钢板高度、厚度和屈服强度或混凝土强度时,BSP梁的相对滑移变形显著增加,钢板与混凝土梁的整体协作能力减弱,但是钢板或混凝土的增强增加了BSP梁的变形能力,因而其受剪承载力有显著提高.
