2018欧洲女子数学奥林匹克第1题探究

江苏省泰州市姜堰区南苑学校 (225500) 江苏省姜堰中等专业学校 (225500)

左小宁 陈 宇

2018欧洲女子数学奥林匹克第1题：在⊿ABC中，CA=CB,∠ACB=120°,M为边AB的中点，设P为⊿ABC外接圆Γ上的一个动点，Q为线段CP上一点，且满足QP=2QC.已知过点P且垂直于线段AB的直线与直线MQ交于唯一点N.证明：当点P在圆Γ上运动时，点N恒在一定圆上.

笔者对这道赛题从解析法角度进行了一番探究.不揣冒昧，奉诸读者.

探究一：别解

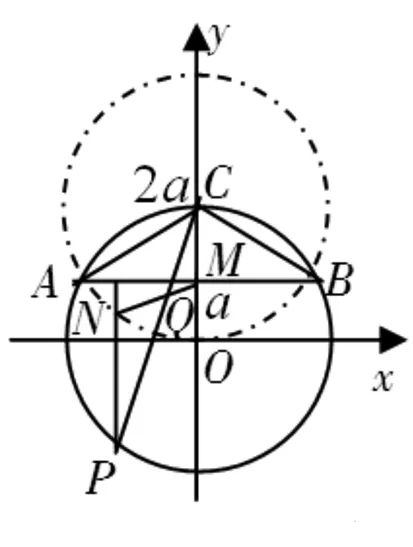
图1

证明：以圆Γ的圆心O为坐标原点，OC为y轴,过O点且与OC垂直的直线为x轴，建立直角坐标系(如图1).设|CA|=|CB|=2a(a>0)，则C(0,2a),M(0,a).圆Γ的方程为x2+y2=4a2.又设圆Γ上的一个动点P的坐标为P(m,n).

由题设知OC⊥AB,PN⊥AB,∴PN∥OC.可得

⊿PNQ∽⊿CMQ.以下法一：

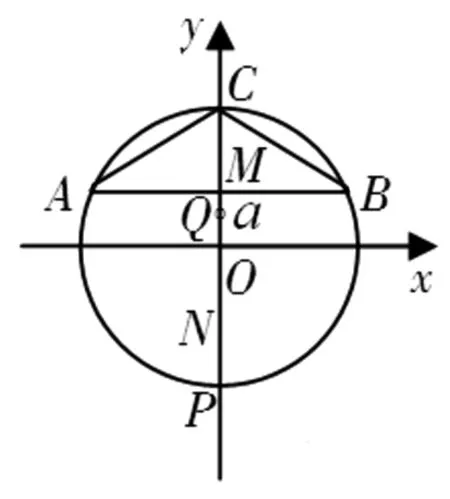
图2

解析法所得动点N的轨迹显然更直观.

探究二：变式1改变点Q的位置，不改变线段QP,QC的大小关系

在⊿ABC中，CA=CB,∠ACB=120°,M为边AB的中点，设P为⊿ABC外接圆Γ上的一个动点，Q为线段PC延长线上一点，且满足QP=2QC.已知过点P且垂直于线段AB的直线与直线MQ交于唯一点N.证明：当点P在圆Γ上运动时，点N恒在一定圆上.

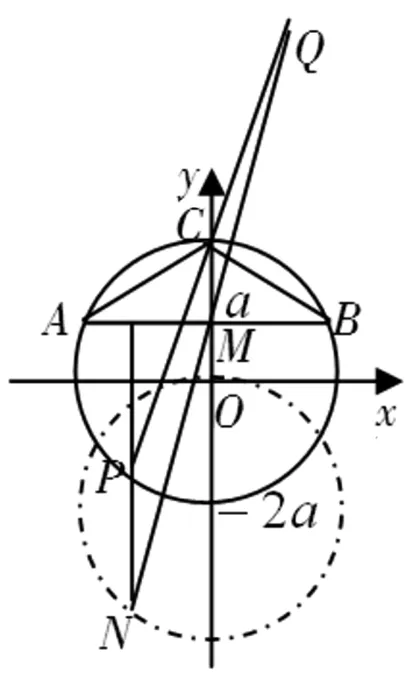
图3

证明：如图3.如上可知，C为线段PQ中点.由中点坐标公式可分别求得xQ=-m,yQ=4a-n⟹xN=m,yN+2a=n.

探究三：变式2 改变点Q的位置，且交换线段QP,QC的大小关系

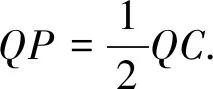
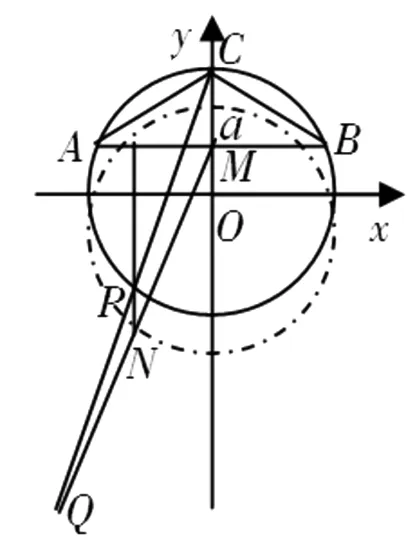
图4

简证：如上可得，λ=

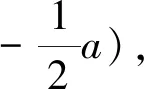
探究四：推广在△ABC中，CA=CB,∠ACB=120°,M为边AB的中点，设P为⊿ABC外接圆Γ上的一个动点，Q为直线PC上异于点C,P的一点，且满足QP=λQC.已知过点P且垂直于线段AB的直线与直线MQ交于唯一点N.证明：当点P在圆Γ上运动时，点N恒在一定圆上.

证明：建立直角坐标系(如别解).设|CA|=

|CB|=2a(a>0)，则C(0,2a),M(0,a).圆Γ的方程为x2+y2=4a2.又设圆Γ上的一个动点P的坐标为P(m,n).

由题设知OC⊥AB,PN⊥AB,∴PN∥OC.可得⊿PNQ∽⊿CMQ.以下法一：

亦可以上述别解二证明之.

相对于解析法，当Q为线段PC上一点时，解析法中λ>0，点N所在定圆为将△ABC外接圆Γ沿OC—y轴向上平移λa个单位所得.

当Q为线段PC或CP延长线上一点时，解析法中λ<0，点N所在定圆为将△ABC外接圆Γ沿OC—y轴向下平移|λ|a个单位所得；

当Q在线段PC上一点，且λ=2时，即为原赛题；

当Q在线段PC延长线上，且λ=2，解析法中λ=-2时，即为本文之变式1；

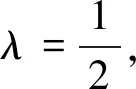
该推广当然可以平几法进行证明—通过分类，参照参考答案的证法.有兴趣的读者不妨一试.当然最后的结论仍然缺少直观性.而借助于解析法，真正体现了数形结合的优势，可以完全直观地看到点N所在定圆的具体位置.当然，对于培养学生思维的求异性，深刻性同样多有益处.