在探究中理解，于理解中探究*——一道课本题的反思与拓展

江苏省兴化市第一中学 (225700)

姜 馨

数学教育的本质就是培养学生用数学的眼光观察世界，用数学的思维分析问题，用数学的思想解决问题.从数学教育的本质上讲，就是要提升学生分析问题，解决问题的能力.积极有效的数学探究活动，有助于促进学生探究习惯的形成，有助于培养学生良好的数学思维习惯、抽象能力及交流合作意识，让学生在探究的过程中不断理解数学的本质，提升数学核心素养.

苏教版选修2-1第37页有这样一条求椭圆离心率与范围的题目，学生在解完之后，觉得意犹未尽，如果能在本题的基础上做一些变动，做一些深入研究是不是更有意思一点呢？本文就是基于这一点和同学们一起开启了探究之路.

1.引例

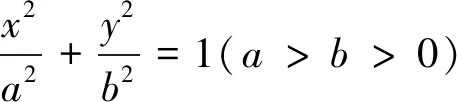
(1)若∠F1PF2为直角，求椭圆的离心率；

(2)若∠F1PF2为钝角，求椭圆离心率的取值范围.

本题清晰自然，点P位置确定，易在具体三角形中求值与求范围，如果将点P改为椭圆上的一个动点，又该如何解决问题呢，不妨做下列探究.

2.探究新知

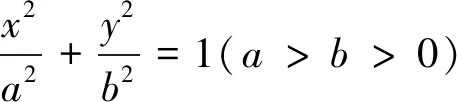
试问1 本题需要先做两个方面的研究，如何理解∠F1PF2=90°？如何理解“存在”？

第四点直角的理解，就是本题的几何解释了，即当椭圆与以F1F2为直径的圆有交点时，存在点P使得∠F1PF2=90°.如图1所示.

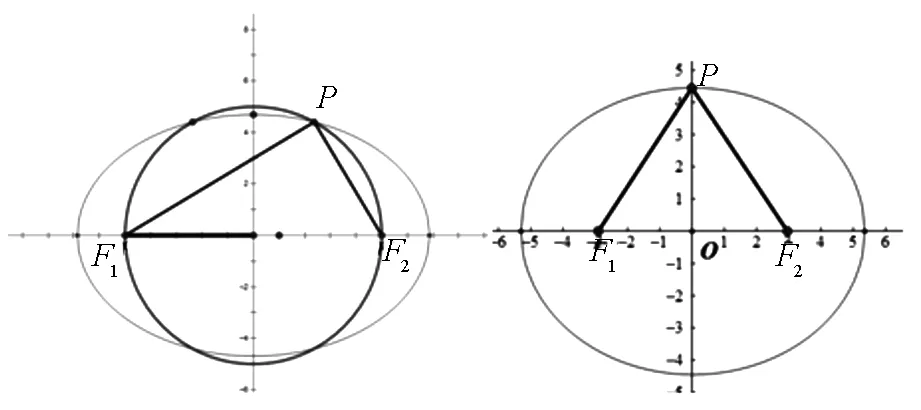
图1 图2

上述的探究过程很好的解决了存在点P的问题，其实问题还可以进一步探究，点P在椭圆上移动∠F1PF2怎么变化呢，有没有一定的规律？

试问2 当点P在椭圆上移动时，∠F1PF2能取到最大值吗？此时点P位于何处？

借助于几何画板，发现当点P由左向右移动时，角先变大，再变小，当点P位于上下端点时角最大，如图2所示.

证明：根据椭圆的定义可知，PF1+PF2=2a，在ΔF1PF2中，∠F1PF2∈(0,π)，由余弦定理得

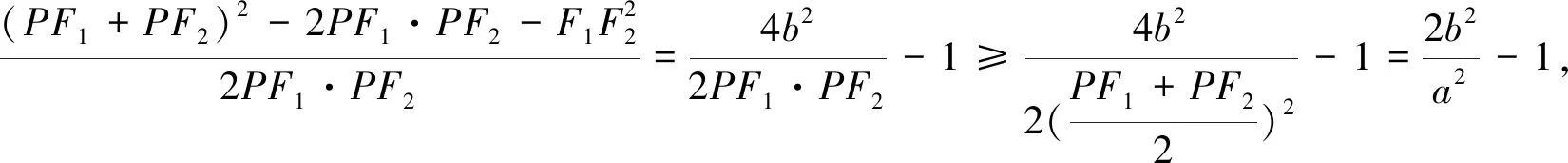
有了这个结论，只需要用一个角就可以“控制”角的变化，即∠F1BF2≥90°时椭圆上就存在了一点P使得∠F1PF2=90°，以“静”制“动”，万变不离其宗.

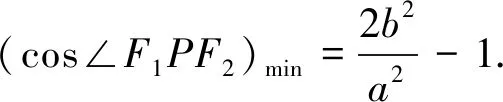
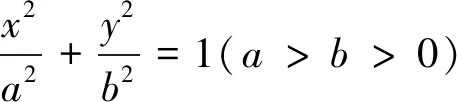
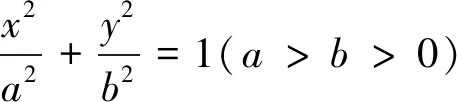
3.拓展延伸

试问3 如果将椭圆的两个焦点换作椭圆长轴的两个端点，这时∠APB的变化情况又如何呢？

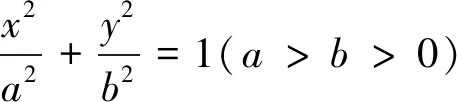
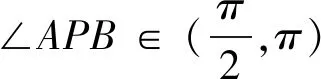
图3

tan∠APB=tan(∠PBx-∠PAB)

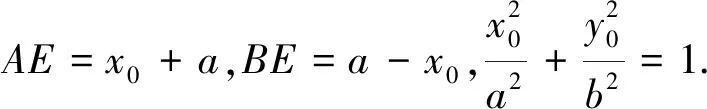
tan∠APB=tan(∠APE+∠BPE)

有了这个结论就同样可以利用“以‘静’制‘动’”的方法来解决上面的问题了.

4.习题教学心得

习题教学，是否有效、高效，深刻地反映出一个教师的专业水平和素养.在习题教学中，教师是学生思维的引领者.教师对问题的理解深度直接影响着学生对问题的认识程度.教师在教学中把握好梯度，由浅入深，引导学生们去探索—理解—应用，在解题中逐步成长.

4.1 在探究中理解

章建跃博士指出，教师在教学过程中要学会理解数学、理解学生、理解教学，学生在学习过程中要理解题目的本质.在上述例题中，学生在探索求解方法时，对题目中的一些关键词是不是真的理解了，如“存在”、“直角”等.“直角”我们如何理解，由直角可以联想到哪些知识点，如何去运用直角这个条件，都需要老师带领着学生去联想、去理解、去体现.“存在”它的含义是什么，是单个存在还是共同存在，要使其存在，是不是只要达到一定的要求就可以了呢？等等这些都需要学生去探索、去理解.在探索中不断完善对知识的理解才是实现学习的真谛.

4.2 在理解中探究

数学的学习过程就是一个需要不断完善的过程，罗增儒教授提出“学会解题的四步骤程式是‘简单模仿、变式练习、自发领悟和自觉分析’”.在对改编1的题目理解之后，是不是就止步了呢？如果条件再发生改变，能不能解决呢？这就需要在理解的基础上再次探索.比如由对PF1+PF2=2a的理解，能否探索PA与PB的内在联系；由∠F1PF2的变化情况能否联想到∠APB的变化情况；由利用∠F1PF2的余弦值为载体证明最大角，能否探索出以何为载体来证明∠APB的最大值.通过问题的再提出，引导学生自发领悟和自觉分析，不断总结，提出新思路，总结新结论，完善对新结论的理解，达到学习的新高度，最终实现在解题中成长，在成长后解题.

4.3 注重核心素养的培养

对于改编题，题目新，通过不断改变点P的位置，观察角的变化，归纳出一般性结论，对归纳的结论进行证明，形成定理，最后再对定理灵活应用.这样的一个完整的研究数学问题的思路，符合学生认知规律，对培养孩子们思维的逻辑性、严密性起到了很好的引领作用.历史上伟大的数学定理的发现都经历了这个过程，本习题的讲解，不但教会了学生如何解题，更教会了学生发现问题、处理问题的方法，培养了学生的核心素养，使学生受益终身.

总之，习题教学应符合学生的身心发展规律，关注数学内容、教学理论、教学实践与核心素养的有机结合，有步骤、有梯度引导学生直面问题，不断探索，让学生从本质上理解数学，从技术上优化数学解题，从方法和思想上发展数学的理性思维，使素养之花在学生的心目中绽放.唯有这样，才能让学生领悟“在探究中理解，于理解中探究”，促进学生不断成长.