一道高三模拟题引发的思考

2019-08-05甘肃省兰州市第二十七中学730030陈鸿斌甘肃省兰州市第五十二中学730030

中学数学研究(江西) 2019年7期

关键词：向量高三运算

甘肃省兰州市第二十七中学 (730030) 陈鸿斌甘肃省兰州市第五十二中学 (730030)

贾丽红

数学教师要善于思考、挖掘、研究,这对反思自己的教学行为和提升学生的数学思维能力具有积极的作用.本文通过对一道高三模拟考试题学生的解答情况进行调研,弄清楚学生思维误区的成因,谈谈自己的一点思考,希望对各位一线教师的教学有所启示.

1.试题呈现

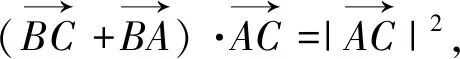
A．等边三角形B．等腰三角形

C．等腰直角三角形D．直角三角形

本题是甘肃省兰州市第二十七中学高三第四次模拟考试第10题,主要考查了核心概念平面向量的加减运算、数量积的含义以及它们的几何意义.从阅卷结果来看,本题得分率很低,绝大多数学生从形的角度出发,但是没有理解数量积的几何意义而进入思维的误区致错,一部分做对的同学则是从数的角度,通过运算求得结果.纵观近几年的高考题,平面向量的问题主要还是以考察数学运算的核心素养为主,但是,学生在训练中总是想走捷径,试图借助于几何意义快速求解,逐渐形成了思维定势而忽略了向量本身的代数特性.这就启示我们在平面向量的教学中,要坚持代数法和几何法两手抓,两手都要硬,从中培养学生数学运算和直观想象的核心素养.

2.思维误区

错误一：大约有50%的同学解答如下:

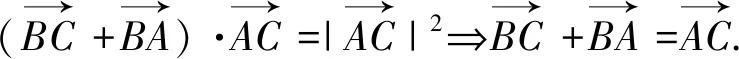
错误二：大约有20%的同学解答如下:

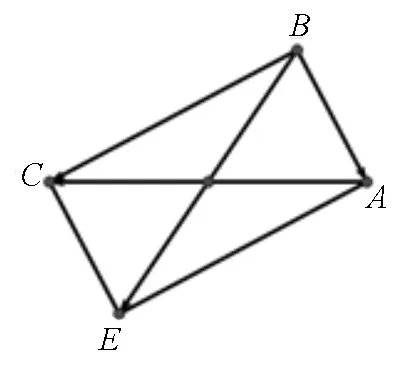
图1

错因分析:这些学生错误的认为平行四边形两条对角线向量的数量积不可能等于一条对角线向量的平方,陷入思维的误区,没有理解数量积的几何意义.反映出学生在学习中往往侧重于形式上的计算结果而忽视知识的背景和几何意义.提示我们在高三教学中要加强对类型题的归类和思辨性,同时仍要重视揭示知识产生的背景和形成过程.

3.正确解答

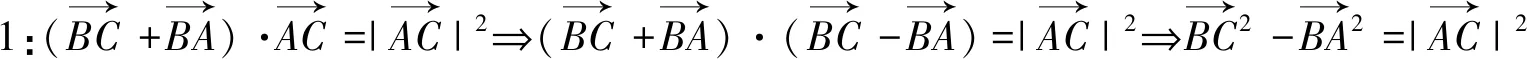
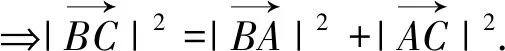
点评:利用解法1解答正确的同学仅占5%,这些学生熟练掌握了向量加减法及其几何意义,理解了平面向量的基本定理和数量积运算,将原问题转化为勾股定理而快速求解,足见其数学素养很好.

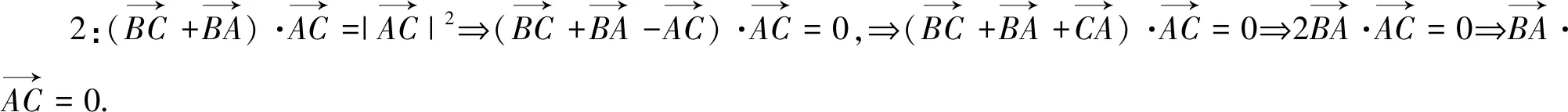
点评:利用解法2正确求解的同学大约10%,这些学生熟练掌握了平面向量的加减法、数量积运算及其运算律,具有良好的数学运算的核心素养,因此培养学生数学运算的核心素养必须长期得以重视.

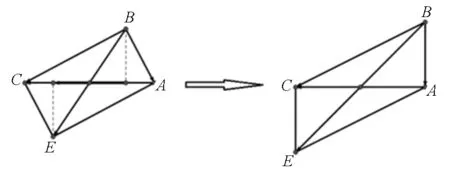
图2

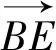
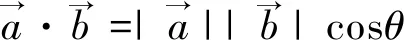
4.“姊妹”题思辨

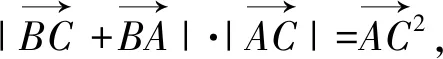
A．等边三角形B．等腰三角形

C．等腰直角三角形D．直角三角形

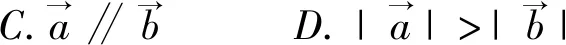
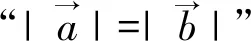
A.充分而不必要条件

B.必要而不充分条件

C.充分必要条件

D.既不充分也不必要条件

此处完全是数的运算,具有消去律.几何法优于代数法，前面“错误一”中的解答就是与这两个题目混淆而不能区分,所以题型的归类和思辨在高三复习中是很重要的.下面求解第(2)题:

解法2:对角线相等的平行四边形是矩形,故选A.

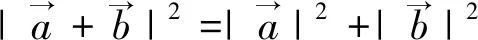
点评：以上4道题与原题属于“姊妹题”,既有区别又有联系,但是这4道题明显几何法优于代数法.通过对“姊妹题”的思辨,将观察与实验、比较与类比、分析与综合、抽象与具体化、概括与特殊化、猜想与反驳这些思维活动探究数学过程的方法贯穿于教学之中,从而培养学生的数学思维能力.

5.一点思考

5.1 注重概念意义的教学

数学中,一切概念的意义是第一位的,而且数学概念的意义是确定而无歧义的,体现了数学的严谨性.这必然要求我们在教学中,特别强调使学生获得明晰的概念意义.从内涵和外延两方面引导学生去理解数学概念,概念的内涵决定了概念的外延,而对概念外延的清晰有利于辨析内涵与外延的关系,防止概念的非本质泛化,促进对概念内涵的理解和把握.

5.2 注重知识的产生背景和形成过程

在高三教学中,往往在大量的解题中多了形式化的计算结果,而缺失了数学知识的背景和形成过程的教学.事实上导致学生思维结果的思维方法是数学学习的方法,也是数学研究的方法,同时还是数学教学的方法,教学活动中应该体现观察与实验、比较与类比、分析与综合、抽象与具体化、概括与特殊化、猜想与反驳这些思维活动的过程.2019年高考数学命题也要求有的试题通过揭示知识的产生背景和形成过程，体现数学的创造、发现和发展特点；有的将通过对数学思维方法的总结、提炼，呈现数学的思想性.