基于元认知理论的高三数学解题教学思考

江苏南通师范高等专科学校 (226000)

梁 瑾

高三第二轮的复习是在第一轮复习的基础上，以专题训练的形式进行查漏补缺，将整个高中的知识点进行提炼、重组，使其网络化、系统化，从而提高解题能力.在这个关键的二轮复习过程中，学科组的老师们可谓费尽心思，使出浑身解数，收效是有的，但却不容乐观.学生解题往往是：解题前缺少对题意的审视和方法的选择、比较；解题过程中缺乏“瞻前顾后”、及时纠错；解题后没有验证答案正确性的意识，更不会自主性的举一反三、触类旁通.

解题教学本质上是一种思维教学，教师不仅要向学生展示“怎样解题”的思维过程，更要向他们渗透“为什么这样解”以及“怎样学会解”的解题认知，从源头上解决问题.

下面通过笔者的一个教学案例具体谈谈高三解题教学的思考.

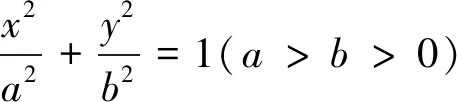
师：这是2012年天津卷第19题第2问，从同学们的完成情况来看，发现很多同学对这个题目不是完全无从下手，但最终能完整做出的却并不多，下面我们就一起来探讨下这个题目.

师：题目要求我们证明直线OM斜率k的范围，大部分同学们都想到设点M的坐标(x1,y1)，表示出斜率k，这是解题的目标意识.本题有两个显而易见的条件：(1)点M是椭圆上的点；(2)|AM|=|OA|.

生：根据这二个条件可以得到以下方程：k2=

我想把x1解出来.但是然后就进行不下去了，(不少同学露出深有同感的表情)，(我深知不少同学是这么做的，这种思路符合学生的思维特点，顺乎一般思维规律，接下来算不下去，被卡了，这时我不能简单的告诉他们如何做，更不能轻描淡写的加以否定.尊重学生的思维，通过提出一些具有指向性的问题进行启发，顺其自然地帮助学生.在教学设计中有时需要采用稚化思维的设计策略.所谓稚化思维，就是教师把自己外在权威隐藏起来，在教学时不以一个知识丰富的教师自居，而是把自己的思维降格到学生的思维水平上，亲近学生，接近学生，有意识地退回到与学生相仿的思维状态，设身处地地揣摩学生的学习水平、状态等以与学生同样的学习情绪、同样的思维情境、共同的探究行为来完成教学的和谐共创.[1])

师：不要被问题的表象所蒙蔽！观察一下方程②，它的真相是？

生：哦，一元二次方程！(学生一下子被点醒，看到了曙光，开始投入运算)

生：利用求根公式得

生：必须化简，但是二个根从哪一个先入手？(学生们嘀咕着)

师：不急着化简，先回头再来观察一下题目，有没有其他条件了？(很多学生解到这里就会中途放弃，这时需要学生学会回头看题，挖掘条件)

生：好家伙，括号里还有个条件a>b>0(学生像发现了新大陆，对自己的发现很兴奋)

师：往往括号里的内容就藏着解题的钥匙啊，这需要我们今后重视！这样我们就可以舍去一个根了，而且还会解决化简问题.

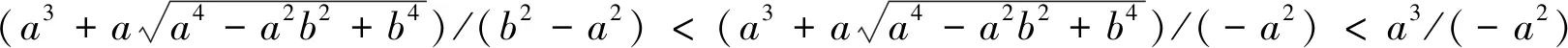
(b2-a2)，则k2=-1-2a/x1=-1+2a/(a3-

师：嗯，胜利就在眼前了！这里舍根使用了放缩的方法，放缩必须要不等关系(及时归纳总结)

生：出现两个变量，不能消元(学生又一次体验了成功的滋味，积极性很高)

师：一定要消元吗？如遇到二个甚至二个以上的变量，我们以往还有什么办法处理？

生：整体思想！整体换元，把a2/b2视为整体,

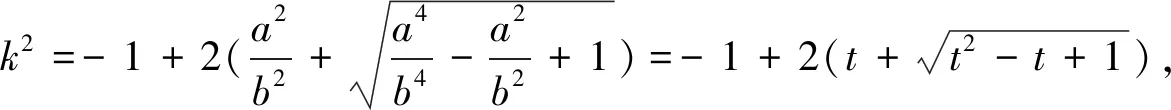
师：这种证法虽然计算量大，但思维较流畅，同学们容易想到，当然这种证法中也有不少难点：一元二次方程的舍根、换元的思想、函数单调性的应用，还有题目中看似不起眼但却是很关键的条件a>b>0的处理.(关注学生的意愿和学习过程中的情绪反应，并充分利用学生的反应，分享学生数学学习情境中的各种努力，呵护好学生的数学幸福感，充分尊重学生的元认知体验，这对学生的学习投入和成绩具有重要的影响.)

师：还有没有其他的方法呢？换个角度叙述条件|AM|=|OA|.

生：|AM|=|OA|=a，说明点M的轨迹是圆(x+a)2+y2=a2.

生：哦！点M既是直线与椭圆的交点，还是直线与圆的交点，这样通过联立方程组，算出点M横坐标(用k表示)从而得到关于k的方程，再根据已知条件a>b>0得到关于k的不等式，就能解出k的范围.

师：逻辑思维很强！要求k的范围，就想得到关于k的不等式……(正确的解题认知要在潜移默化中传递给学生)

学生甲出示了他的解题过程:

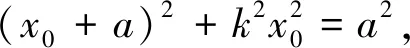
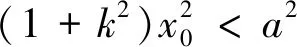
师：嗯,你的解法也很好！这两种解法的本质是一样的，都是在x0和k之间找到桥梁，由条件a>b>0产生不等关系.这种解题的思路方法或应纳入我们的解题认知结构中去.

(数学问题解决的教学中，要善于通过“多解归一”的方式，寻求不同解法的共同本质，乃至不同知识类别及思考方式的共性，最好能上升到思想方法、哲理观点的高度，从而不断地抽象出具有共性的数学方法，让元认知的统摄作用有了真正的着落点.)

师：要实现目标求k的范围，有时我们也可以将问题转嫁，正难则反嘛.

师：这个问题变得有趣了！如何得到x1的范围？大家讨论一下(学生的积极性高涨，投入激烈的讨论中)

师：这位学生解题时有较强目标意识，牢牢抓住目标与结论的差异与联系，优化解法的同时大大减少了运算(教师在教学过程中，可以引导学生采用目标意识(一种元认知意识)，即抓紧目标，从要证明的结论出发，考虑要得到结论所需要的条件，这些条件能否直接从已知条件来？有没有隐含条件？即从已知条件变形、转换、推理过来.如果这样还是不行，则考虑进行调节，将结论变形，化归成一个熟悉的问题.在学生的解题过程中，引导他们主动地进行自我监控和调节)

这时教室后面一只手高高举起.

师：你的观察很敏锐！也就是我们还可以考虑数形结合的方法来处理

生A:可以先考虑∠AOM的范围,需要将它放入一个三角形中，而且最好是直角三角形，如何构造一个直角三角形呢？

学生B在下面轻轻的提示：|AM|=|OA|.

师：想法很棒！可以说是另辟蹊径，出奇制胜！

师：解题后的总结和反思是我们每个同学都必须养成的习惯，它有比解出题目更深远的意义.

生：证法1通过寻找k和x1之间的关系将问题转化为函数的单调性问题来求解.

生：证法2对结论进行追根溯源，找到解决问题的简便方法，对我很有启发.

生：证法3和证法1的本质是一样的.

生：证法4利用了k的几何意义，借助三角函数的单调性利用数形结合的方法.

生：我想应该还有别的方法，但不管哪种证法，条件a>b>0的放缩使用都起到了关键的作用，是解这道题的突破口.

师：同学们都总结的很到位！今天我们共同学习了这一道题，相信大家一定有不少的收获.希望我们同学能通过这道题的共同探究找到数学解题的感悟.

“数学是思维的体操”，解题教学就是要教会学生去思考，培养学生自主、合作、探究的学习方法，积累学生的解题认知，形成自我监控的意识和习惯，这是我们解题教学的硬道理.