基于混合局部搜索方法的大规模车辆路由问题求解研究
2019-08-03罗海峰
罗海峰
(安徽工业职业技术学院 信息工程系,安徽 铜陵 244000)
车辆路由问题(Vehicle Routing Problem,VRP)由Dantzig于1959年提出,其目标是寻求最优的路径集合,使得所有客户均被服务的前提下,车辆的运输费用最小化[1]。因其广泛的应用背景,如银行现金配送、邮件配送、校车调度、安全巡逻服务等[2],VRP被众多科研机构和学者关注和研究,并提出了一系列的用于求解VRP的算法,如精确算法、分枝定界、动态规划等[3]-[4]。
VRP是一类典型的组合优化问题,属NP-hard问题,上述确定性等算法往往只能解决规模较小的问题,一般不超过150的客户数。随着问题规模的增加,问题的解空间呈指数级扩大,即所谓的问题爆炸现象。面对巨大的解空间,如何正确地引导搜索方向,在有效的解区域中寻找优秀解,是目前关于该问题的研究重点。针对规模较大的VRP问题,目前已有较多求解算法,较典型的有启发式算法[5]-[6]。然而,现有启发式算法中多数基于传统的局部搜索,对于当前的个体,在较小范围内进行邻域搜索。所以,若进行充分的邻域探索,得到较高质量的邻域解,则需要多次启动局部搜索。针对上述邻域搜索尺度较小的问题,Vidal等人提出了大规模邻域搜索(Large Neighborhood Search,LNS)算法,对相应的VRP问题进行求解,并取得了较好的效果。大规模邻域搜索的基本思想是在当前解中选取若干客户构成待分配客户集合,并将它们从解中删除,然后为待分配集合中的每个客户寻找理想的插入位置,重新安置。如此,LNS能够在较大范围内对个体解进行邻域搜索。显然,传统的局部搜索较精细,而LNS侧重于全局性。因此,针对大规模VRP的特点,结合传统局部搜索以及LNS的优势,本文设计了一种混合局部搜索方法(Hybrid Local Search Approach,HLSA),首先对个体进行传统的局部搜索,如单客户插入、交换、2-opt等,然后再进行大规模的局部搜索,以寻求优质解。
1 车辆路由问题模型
1.1 VRP问题描述
基本VRP在实际的应用,将面临众多约束,如车辆的负载、最大行程等。本文旨在对车容量受限的VRP(Capacitated Vehicle Routing Problem,CVRP)进行分析和求解,并且考虑车辆的最大行程。
CVRP可描述为存在n个客户需要被服务,停车中心停放了K辆容量为Q的服务车辆。现要求K辆车为客户提供服务,在所有客户均被服务的前提下,车辆的总运输费用(total cost, tc)达到最小化,并满足约束:(1)每个客户均被服务一次,且只能被一辆车服务;(2)车辆从停车场出发,最后回到停车场;(3)每辆车上的客户总负载量应满足容量约束Q;(4)每辆车的行程不能超过最大距离D。
1.2 VRP问题模型
给定无向连通图G=(V,E),其中V是顶点集,由n+1个元素{v0,v1,v2,…,vn}组成,元素v0代表停车场,vi(1≤i≤n)代表第客户i,对应的服务需求量为qi,其坐标为(xi,yi);E为边集,每条边代表一通路,边eij=(vi,vj)的长度为disij,亦代表车辆通过此边的运输费用,可通过下述公式计算,即:
(1)
停车场v0存有容量为Q的K辆服务车,每辆车的最大行程距离为D。同时,为了问题描述方便,定义如下二值变量为:
(2)
(3)
CVRP的目标为:
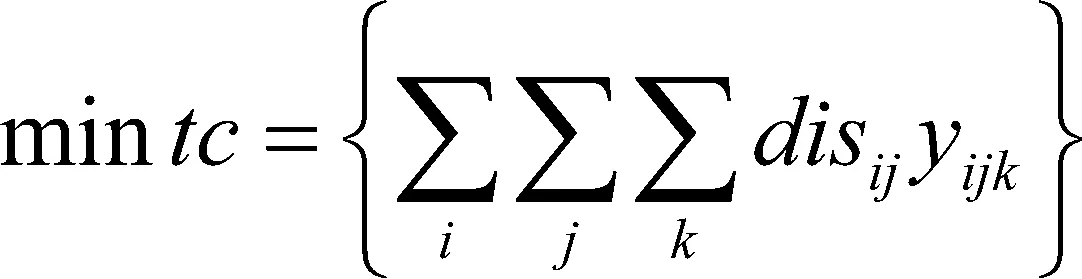
(4)
同时,需要满足以下约束条件,即:

(5)
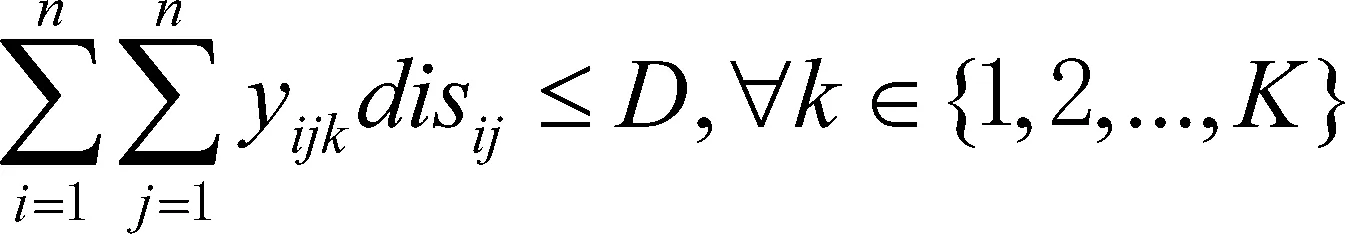
(6)
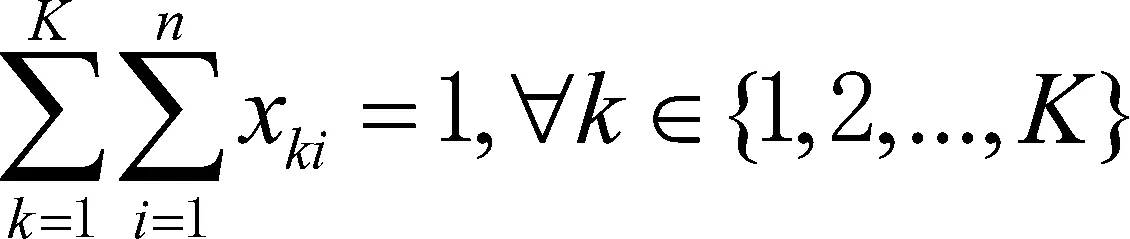
(7)
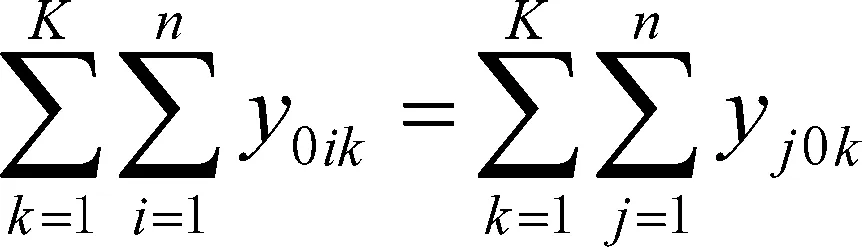
(8)
其中,约束(5)确保每辆车的负载不超过容量限制Q,约束(6)要求车的最大行驶长度不超过D,约束(7)则使得每个客户被服务一次,仅一次,式(8)则保证车辆由停车场出发,最后回到该停车场。
2 混合局部搜索方法设计
2.1 局部搜索
对于给定的解s,按照既定的策略,对其邻域进行搜索,以获取更优的解。这种搜索,实际上就是根据搜索策略形成的规则,对解s的结构进行局部调整,若发现调整后的解较原来的解s好,则认为搜索是成功的,替换s。通常此过程一直持续到不能发现更优解为止。大致框架如下:
Step 1: 对解s按照一定规则搜索邻域,得到邻域解s′;
Step 2: 若邻域解s′较s好,也就是f(s′)
Step 3:若结束条件不满足,则转Step 1,继续搜索;否则结束。
这里,f(s)为解的函数值,对于CVRP,可以设定为车辆运输总费用tc。
局部搜索的规则决定了搜索尺度,对于CVRP而言,传统的局部搜索通常只对少数客户进行位置调整,甚至仅一个客户,这样的搜索方式对于规模较大的CVRP问题而言,显然是不够的。所以大规模邻域搜索LNS是传统局部搜索很好的补充。
2.2 LNS设计
大规模邻域搜索的主要问题在于:(1)待分配客户的选取,这些客户在现有解中应是影响解质量的,所以选取、重分配,则有利于发现更好的解;(2)客户重分配,如何对被选取的客户重新安排到某一车辆对应路径的合适位置上,使得所产生的运输费用的积极意义变化量最大,是客户重分配阶段的目标。这是LNS需要解决的主要问题,也是其两个重要阶段。
对于客户的选取,则可通过对现有解中每个客户依据一定规则进行评估,然后挑选。如文献五考虑了客户的需求量、客户从现有解中删除后的tc差值等[5]。客户重分配则可采用典型的最优插入策略(Best Insertion Heuristic, BIH)进行,此策略搜索所有车辆对应路径上的所有位置,在最优处进行客户插入。本文设计的LNS可描述如下:
Step 1:size=size_L;
Step 2:对于解s中的每个客户i,计算其选取值(select value,sv),sv=dem(i) / Δ(i, tc);
Step 3:根据Step 2中客户评估值sv,采用轮盘赌的方式选取size个客户,构成待分配集合AS,并将AS中的所有客户从解s中删除,sv小的客户具有较大概率被选中;
Step 4:将AS中所有客户按随机的顺序,使用BIH策略,插入到中,形成新的解s′;
Step 5:若f(s′)
Step 6:size=size + 1;
Step 7:若size
算法中,size_L和size_U待分配客户集合AS中元素个数的阈值,且AS中客户的选取采用轮盘赌的方式,这样能有效避免选取sv最小的客户所导致的搜索单一性。
2.3 传统局部搜索算子的选取
目前,关于VRP的传统局部搜索算子,本文选取如下算子形成局部搜索算子集合,对现有解的邻域进行搜索。
(1)单点插入(Single Insertion,SI)算子,将某一客户从当前位置删除,在所有路径中寻找更好的位置,进行插入;
(2)双点插入(Double Insertion,DI)算子,类似SI,区别在于操作对象是相邻的两个客户;
(3)交换(Swap)算子,选取一对客户,交换他们的位置;
(4)2-Opt,存在两种形式,同一路径中,逆序某一客户子序列;两条不同路径各自设置断点,进行子路径对接;
(5)3-Opt,两条不同路径分别被分割成三段,然后交换中间的客户子序列。
以上SI、DI以及Swap可以是基于某一车辆对应的路径,也可以是不同路径间的操作。
2.4 混合局部搜索方法
基于上述LNS以及传统局部搜索算子集合,本文所设计的混合局部搜索方法HLSA流程如下:
Step 1:依据车辆的容量限制Q,随机初始化解s;
Step 2:final=s,cur=s;
Step 3:iter=1;
Step 4:t =cur;
Step 5:对t采用2.3节中的传统局部搜索算子进行邻域搜索,在较小范围内寻求更好的解;
Step 6:对t采用2.2节中的大规模邻域搜索算子LNS进行搜索,在较大范围内寻求更好的解;
Step 7:如果f(t)
Step 8:若f(t) ≥ f(cur)成立,且连续没有改善的代数超过Jump次,则算法结束,否则若连续无进展的迭代次数超过Diversity且f(t) 较 f(s)不超过5%,则base=t;
Step 9:iter=iter + 1;
Step 10: 如果iter ≤ Max_Iterations,则转Step 4继续执行,否则算法结束。
算法中,Step 8主要避免盲目执行毫无进展的迭代以及搜索陷入局部最优,Max_Iterations为最大迭代次数。
3 实验结果及分析
3.1 实验准备
为了验证本文所设计的混合局部搜索方法HLSA在大规模CVRP问题上的有效性,我们采用文献五中的国际基准测试数据,其中规模最小的样例中客户数为560,最多的为1200,较之前的测试数据规模有很大的提升。对于客户数1000以上的样例,均被选中运行,而1000以下的,则挑选有代表性的测试样例,如Li-21、Li-23、Li-25、Li-27以及Li-29等。
文中以Visual C++ 6.0为工具,编程实现HLSA。运行环境为Linux系统,CPU Intel Core i5-7500,主频3.4 GHz,内存8GB。参数设置,多样性参数Diversity=300,提前终止迭代参数Jump=5×Diversity最大迭代数Max_Iterations=10000。
3.2 运行结果
HLSA以及文献六中的VRTR在基准测试集上的运行结果如下表所示,表中参数A、B决定客户数n,n=A×B,veh为停车场中驻留的可用车辆数,Q、D分别表示车辆的最大负载容量和最大行程[6]。ratio表示HLSA相对于VRTR对应结果的优化率,可按下述公式计算为:
(9)
由上表可以看出,在选取的8个测试算例上,本文所设计的HLSA取得了7个较VRTR好的结果(较好解以粗体标出),占有率为87.5%,最高优化率为2.32%,仅算例Li-29稍劣于VRTR。尤其值得注意的是,HLSA对于问题规模超过1000的所有算例,均取得了较VRTR好的结果,说明了HLSA对于大规模CVRP的有效性。另外,8个测试样例结果的均值中。VRTR的值为25566.47,明显高于HLSA的结果(25387.73),平均优化率为0.76%。
4 结束语
本文就大规模容量受限的车辆路由问题CVRP,设计了一种混合局部搜索方法HLSA对其求解。算法中,利用传统局部搜索策略以及大规模邻域搜索LNS的各自所具有的优势,将它们整合在一起。在大规模基准测试数据上的结果,表明HLSA能够较好地处理大规模CVRP问题。
