混合式永磁耦合调速器导体转子振动研究
2019-08-01陈明丰李剑峰朱洪波佟永吉
陈明丰,李剑峰,朱洪波,姜 涛,佟永吉,杨 柏
(1.国网辽宁省电力有限公司,沈阳 110004;2.沈阳工程学院, 沈阳 110136)
0 引 言
随着科技的快速发展,近年来许多专家学者针对永磁调速器振动问题展开了一系列的研究,并且取得了一定的研究成果。文献[1]对于具有相同外形尺寸和磁路尺寸,磁极数目不同对永磁调速器振动的影响,研究得出随着磁极数目的不断增大,振动速度逐渐减小。永磁调速器的关键是其磁路结构设计及传递磁力转矩的准确计算,并保证整机满足热稳定性[2]。近年来,国内已有学者对永磁调速器建模方法、有限元分析及数值仿真计算、结构设计等方面进行了研究。杨超君等[3-4]进行了双层实心和鼠笼转子异步磁力联轴器的涡流传动特性分析;王旭等[1]研究了盘式永磁调速器的磁路结构设计;李桃等[5]建立了基于三维运动涡流场的盘式永磁联轴器的有限元模性分析了其机械特性。
目前,对于永磁调速器的研究多集中在基于盘式或筒式单一结构下的磁场和涡流场分析上。本文研究一种混合式永磁调速器结构,这种混合式结构既具有径向磁路,又具有轴向磁路,可增大永磁调速器的转矩和功率密度。但这种混合式结构是否会对永磁调速器的振动效果产生影响,有待研究。大多数文献都是研究永磁体转子对永磁调速器振动的影响,很少有文献研究导体转子对永磁调速器振动影响。
本文以一种混合式永磁耦合调速器的导体转子为模型,以Sander薄壳理论为基础,分析轴向导体转子,径向导体转子作为对轴向导体转子一端的约束条件。建立三维运动振动的数学模型,利用有限元仿真软件研究了永磁耦合调速器导体转子(径向导体转子与轴向导体转子)振动特性的影响。通过仿真与实验验证了计算方法的正确性。
总体上来说,百日咳报告的年均发病率从免疫规划实施前阶段(1954—1979年)的148.57/10万下降至实施后阶段(1980—2017年)的11.28/10万,下降了92.41%,报告病例数下降83.00%。随着免疫规划的不断普及深入,台州市百日咳的年均发病率呈现不断下降趋势(χ2=247 187.457,P<0.01)。
1 永磁耦合调速器工作原理及其结构
1.1 永磁耦合调速器结构
永磁调速器是一种利用导体盘与永磁盘间磁场的相互作用,从而传递电机与负载之间扭矩的一种机械装置,通过气隙实现调速过程[6]。根据永磁调速器结构不同大体可分为两类,一类为盘式永磁调速器;另一类为筒式永磁调速器[7]。
混合式永磁调速器导体转子可分为环形转子和盘形转子,两部分组成一个筒形结构,通过轴套安装在输入轴上并随之旋转。其中环形导体转子由铜环及其支撑钢环组成,盘形导体转子由铜盘及其支撑钢盘组成。永磁转子也由环形和盘形两种转子结构组成,伸入导体转子内部,浮动安装在输出轴增设的轴段上。其中环形永磁转子由铝环、弧形永磁体及其支撑钢环组成,弧形永磁体径向充磁且N,S极交替放置。盘形永磁转子则由铝盘、矩形永磁体及其支撑钢盘组成,矩形永磁体轴向充磁且N,S极交替放置。永磁体与导体之间隔有气隙。当电机带动导体转子旋转时,拉动永磁转子随之同向转动,再由轴段将转矩传递给输出轴。混合式永磁调速器的调速装置通过拉动永磁转子在销轴内沿轴向移动,改变盘形转子间的气隙长度以及环形转子间的重叠面积,从而调节混合式永磁涡流耦合器的输出转速/转矩,达到调速节能的目的。混合式永磁调速器结构如图1所示。

(a) 外壳

(b) 转子
1.2 混合式永磁涡流耦合器优点
本文研究了一种混合式永磁涡流耦合器,它采用了径向与轴向分别充磁的双向结构。电动机的输出转矩分别通过轴向与径向两个方向传递给负载轴,极大提高了输出转矩的传递效率。与传统的单向永磁涡流耦合器相比,混合式永磁涡流耦合器有以下优点:采用了双向调速,其转矩传递效率更高,节能效果更好;在相同的空间内有着更高的工作效率,提高了空间利用率;发生单一的径向或者轴向故障时,系统仍然可以运行,提高了运行的容错性。
通过示范区建设,加强农业基础设施,改善农民的生产、生活条件,扩大农机化服务功能,提高了科技对农业的贡献率,并通过技术培训,使农民的科技文化素质得到提高。
2 振动特征分析
2.1 建立径向导体转子振动模型
本文所建立的径向导体转子数学模型如图2所示,设径向导体转子半径为b,厚度为H1,F为径向
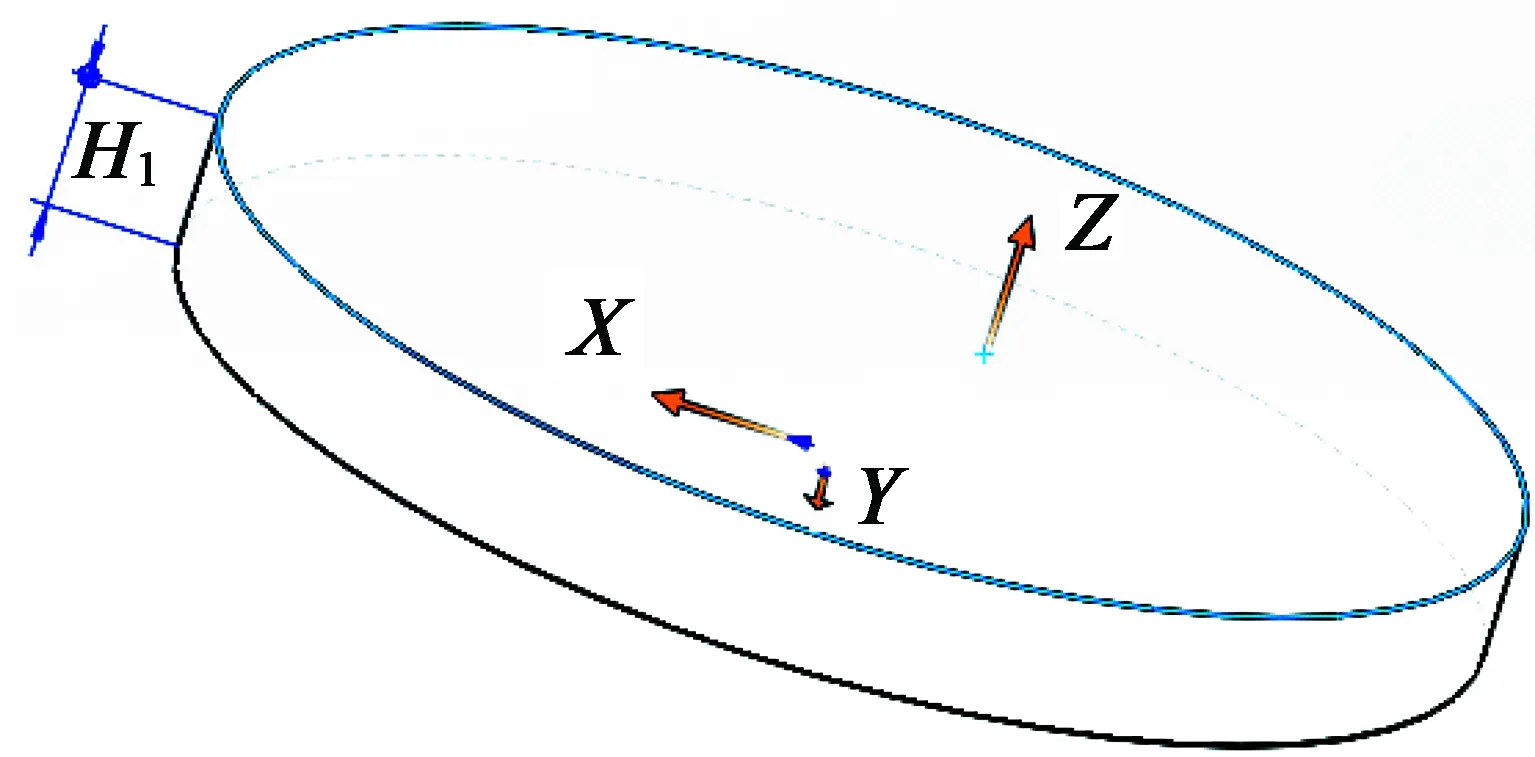
图2 径向导体转子几何参数及坐标系
导体转子所受的外力,导体转子角速度为φ。在极坐标系下建立径向导体转子运动方程:
(1)
(2)
(3)
轴向导体转子约束势能:
(1)突出环境照明。所谓的突出环境照明,又可以称之为基础照明,是指整个展示现场的空间照明。整个环境明亮,展示空间和展品的细节都能清晰的展现。展区的面貌和气氛可以由灯光改变,不同的灯光营造不同的展区效果,柔和灯光让人舒适,延缓视觉疲劳;强烈灯光突出展品,让参展这印象深刻。突出环境照明的基础照明可用直接光源,也可以用间接光源,需根据展示的需要和类型而定。
(4)
本文对混合式永磁调速耦合器的导体转子仿真分析是在设备处于不同转速以及导体转子在轴向移动过程时进行的。利用有限元仿真软件SolidWorks,建立仿真模型,分析仿真结果得出影响永磁调速器振动因素[11]。
上世纪八十年代,邓小平曾经提出体制改革的设想;近年中央纪委研究室也曾指出,影响反腐败成效,体制障碍是最大的障碍,机制缺陷是根本的缺陷。那么涉及到体制改革,诸如民主与法治、土地产权、知识产权、权力的监督与限制等体制上的问题,现在仍然存在着种种不同的认识,影响相关领域改革的深化。
(5)
(6)
(7)
由式(5)、式(6)与式(7)联立可得径向导体转子的振动方程:
(8)
此外使用狄恩数来分析爬坡管段的湍流流动变化。狄恩数为流体流经弯管时的离心力与黏性力之比,其数值等于雷诺数与管道半径、弯头曲率半径比的平方根之积[8],其表达式为
对材料力学性能测试是根据GB/T 228.1-2010的要求进行单拉实验,实验在EHF-UV200k2-070电液伺服疲劳试验机上进行。实验结果取3根试样结果的平均值。
2.2 建立轴向导体转子振动模型
计算时假设永磁体转子与导体转子为圆柱形的壳体,一系列在时间上呈周期性变化的r阶力波沿圆周均匀地分布在永磁体转子上。利用有限元软件建立永磁体转子与永磁体转子的简单模型进行三维模态仿真,得到2≤r≤5 阶模态和振型[10]。力波阶数r≥2时的固有振动频率:
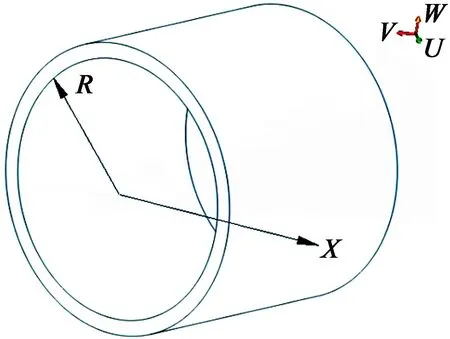
图3 轴向导体转子几何参数及坐标系
径向导体转子振动方程式(8)的解:

(1)还有别的原因么?校内几个人的模型是不同的,你该原谅他们,他们中有的实在是可怜——无聊而又无聊的。
εr=[Dg1(Kr)+Gy1(Kr)]ejξt
(9)

径向导体转子对轴向导体转子约束:
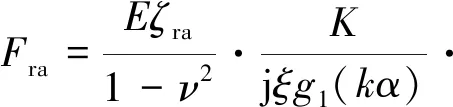
(10)
轴向导体转子任意一点位置矢量:
根据单亲子女的心理特征及问题表现,作为一名高中学生学生工作者,有责任从以下几个方面做好单亲家庭学生的心理教育工作:
她也微微一笑,接过他递来的牛奶,啜进口中。他是想说想念么?她僵硬了一整个星期,168个小时,10080分钟,604800秒的心,就在他的微微一笑之后,顷刻间融化了。变成一滩柔软的水,灌溉了她的血液,让她周身都温暖起来。她也很想他啊。她很想知道他在那一周中的每一秒钟是怎样度过的。吃了什么,和谁吃的,睡得好么,和谁睡的。工作顺利么,画了多少图?
α=ui+vj+ωz
(11)
式中:i,j,z分别为(x,θ,r)方向上的单位矢量。轴向导体转子的功能:
φ2(v2+ω2)]Rdxdθ
(12)
式中:εr,εθ,εz分别为径向导体转子振动位移分量;Γr,Γθ,Γz,Γrθ,Γrz,Γθz为径向导体转子各应力分量,导体转子应变与位移的关系式如下:
(13)
轴向导体转子振动位移函数:
(14)
式中:Un(x),Vn(x),Wn(x)为位移函数。
由于轴向导体转子所受的约束力是任意的,因此,采用改进的傅里叶级数对两个方向上的轴向导体转子位移进行展开:
(15)
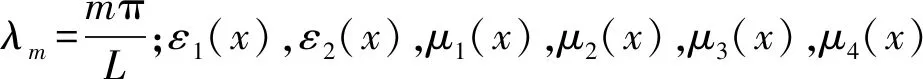
由上述理论及其永磁调速器其他参数估算,确定径向导体转子厚度范围为5 ~10 mm时振动效果最小。虽然利用上述理论估算出了径向导体转子的厚度范围,但仍需要有限元仿真软件来确定最理想的径向导体转子厚度。

2.3 固有频率计算
物体的固有频率仅由物体自身性质所决定,与外部条件无关,它由一组模态参数(固有频率、模态振型、模态阻尼比等) 定量描述,实际中可通过无阻尼自由振动方程计算得出[8-9]。
本文所建立的轴向导体转子数学模型如图3所示,导体转子角速度为φ,导体转子厚度为H,长为L,导体转子内径为R,正交曲线坐标为(x,θ,r)的导体转子在x,θ,r上的位移分量分别为u,v,ω。导体转子的材料密度为ρ,泊松比为μ。由于导体转子是由径向与轴向转子两部分组成,径向转子与轴向转子左端接触连接,因此,径向转子对轴向转子具有边界约束。
由于熔渗温度不同,反应熔渗制备的C/C-SiC复合材料的理论熔渗高度也不同,从而SiC理论含量不同。Yang等[16]在Washburn公式的基础上进行改进,得到了计算理论熔渗高度为:
式中:E为弹性模量;m为转子平均半径处的单位表面质量;hf为转子的径向厚度;Rf1为转子平均半径。由上述分析可知,在其他条件不变的情况下,转子的径向厚度越大,其固有振动频率越高。
3 有限元仿真分析
式中:ζr,ζθ,ζz为径向导体转子轴向应变。
2)在本研究中,商品价格对医药B2C平台顾客忠诚度的影响值为 0.23,相对其他影响因素而言最低。对于顾客而言,商品价格能影响顾客做出的选择,但并非主要因素。
3.1 轴向导体转子有限元仿真分析
对轴向导体转子在不同转速下进行有限元仿真,分别得到转速为1 000 r/min,1 500 r/min,2 000 r/min,2 500 r/min时,轴向导体转子的振动仿真结果如图4所示,轴向导体转子在不同转速下的振动质量参与系数表如表1所示。

(a) ν=1 000 r/min

(b) ν=1 500 r/min

(c) ν=2 000 r/min

(d) ν=2 500 r/min

转速ν/(r·min-1)KXKYKZ1 0002.424 5×10-80.716 460.716 511 5002.471 1×10-80.716 500.716 552 0002.538 9×10-80.716 530.716 592 5002.632 1×10-80.716 610.716 60
对图4与表1进行分析,初步可以得到结论如下:轴向导体转子整体振动幅度不大,转速与振动质量参与系数成正比。转速增大,振动质量参与系数增大,但是增加量极小。轴向导体转子在不同转速下振动质量参与系数几乎相等。
3.2 径向与轴向导体转子有限元仿真分析
图5是在轴向导体转子的左端加入径向导体转子时,不同转速对应的导体转子振动仿真。表2为导体转子在不同转速下的振动质量参与系数。

(a) ν=1 000 r/min

(b) ν=1 500 r/min

(c) ν=2 000 r/min
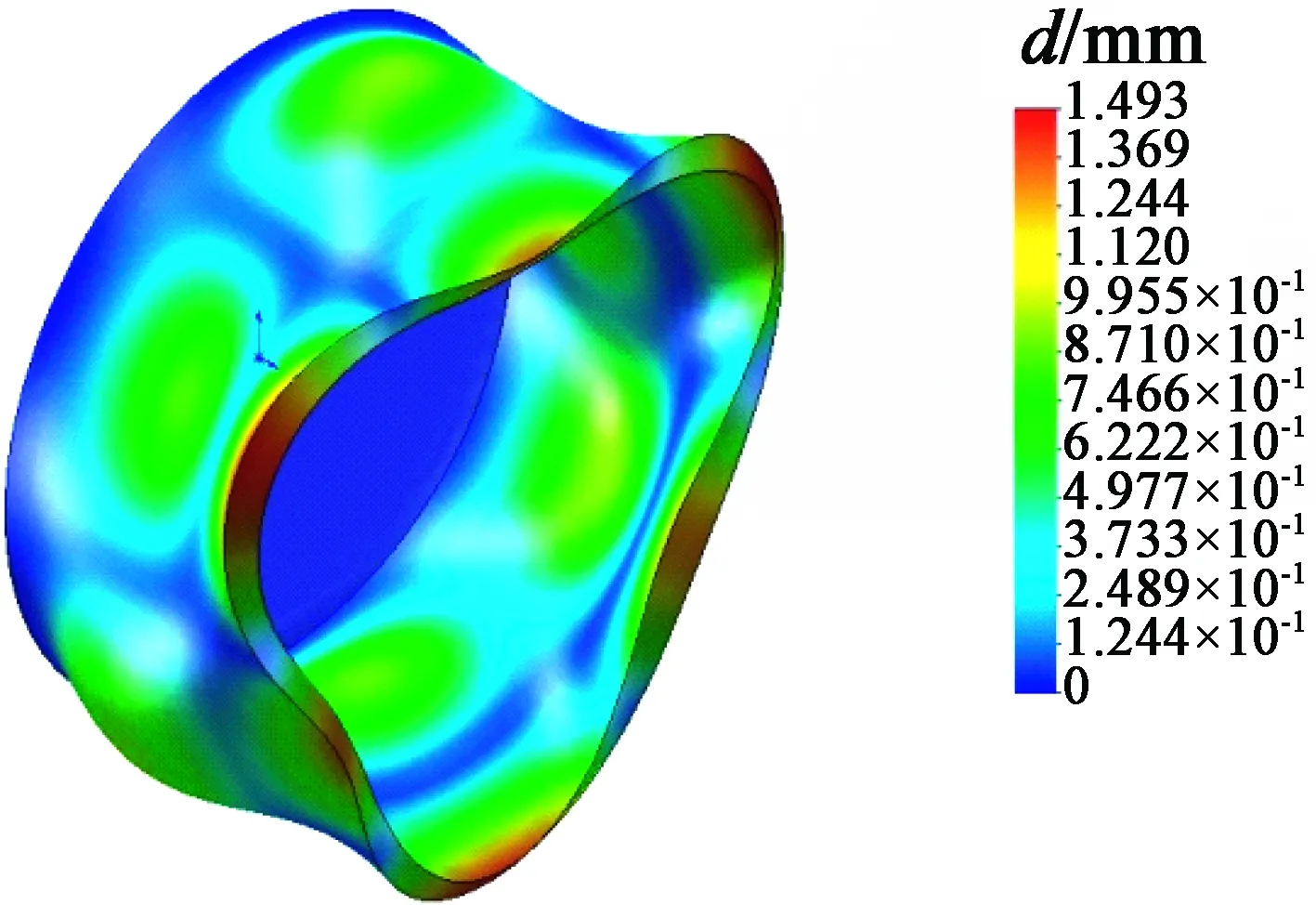
(d) ν=2 500 r/min
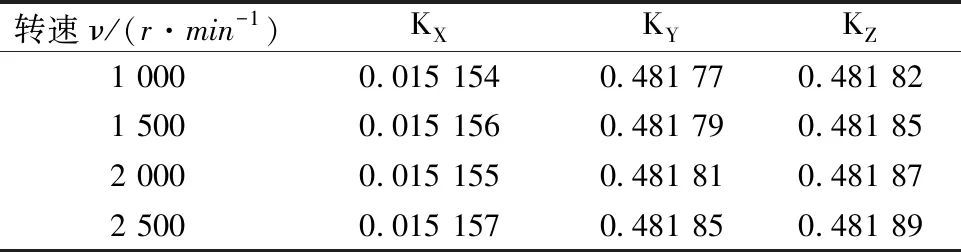
转速ν/(r·min-1)KXKYKZ1 0000.015 1540.481 770.481 821 5000.015 1560.481 790.481 852 0000.015 1550.481 810.481 872 5000.015 1570.481 850.481 89
对表1与表2进行分析,初步可以得到结论如下:径向与轴向导体转子X方向振动参与系数远大于轴向导体转子,这是因为单独的轴向导体转子X方向的;径向与轴向导体转子Y方向与Z方向振动参与系数远小于轴向导体转子,这是因为在轴向导体的左端添加一个径向导体转子,径向导体转子对轴向导体转子在Y方向与Z方向存在约束力F;转速增大,振动质量参与系数增大,但是增加量极小;径向与轴向导体转子在不同转速下振动质量参与系数几乎相等,则导体转子在稳定运动状态下约束力F对导体转子在不同转速下振动的影响甚小,可以把约束力F看作常数。
3.3 不同厚度的径向与轴向导体转子在不同推进位置的有限元仿真分析
对不同厚度的导体转子在处于不同推进面积(1/3,2/3和3/3)时,针对不同的转差作振动分析,如图6所示,其目的在于分析导体转子振动特性,以便于寻找设备的最佳工作状态,规避对设备造成损坏的不利运行状态,并进一步确定导体转子振动最优尺寸。
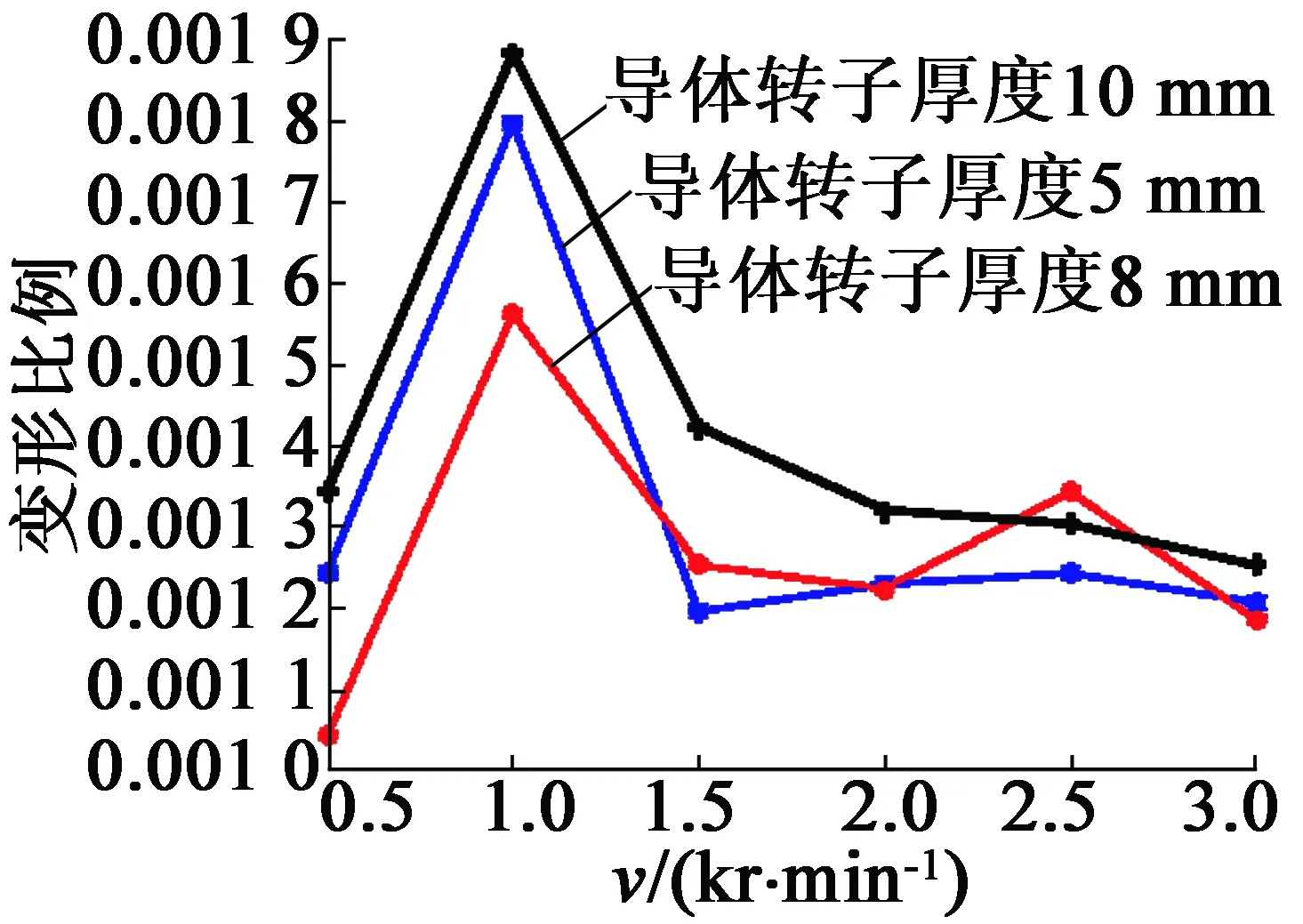
(a) 推进面积为1/3
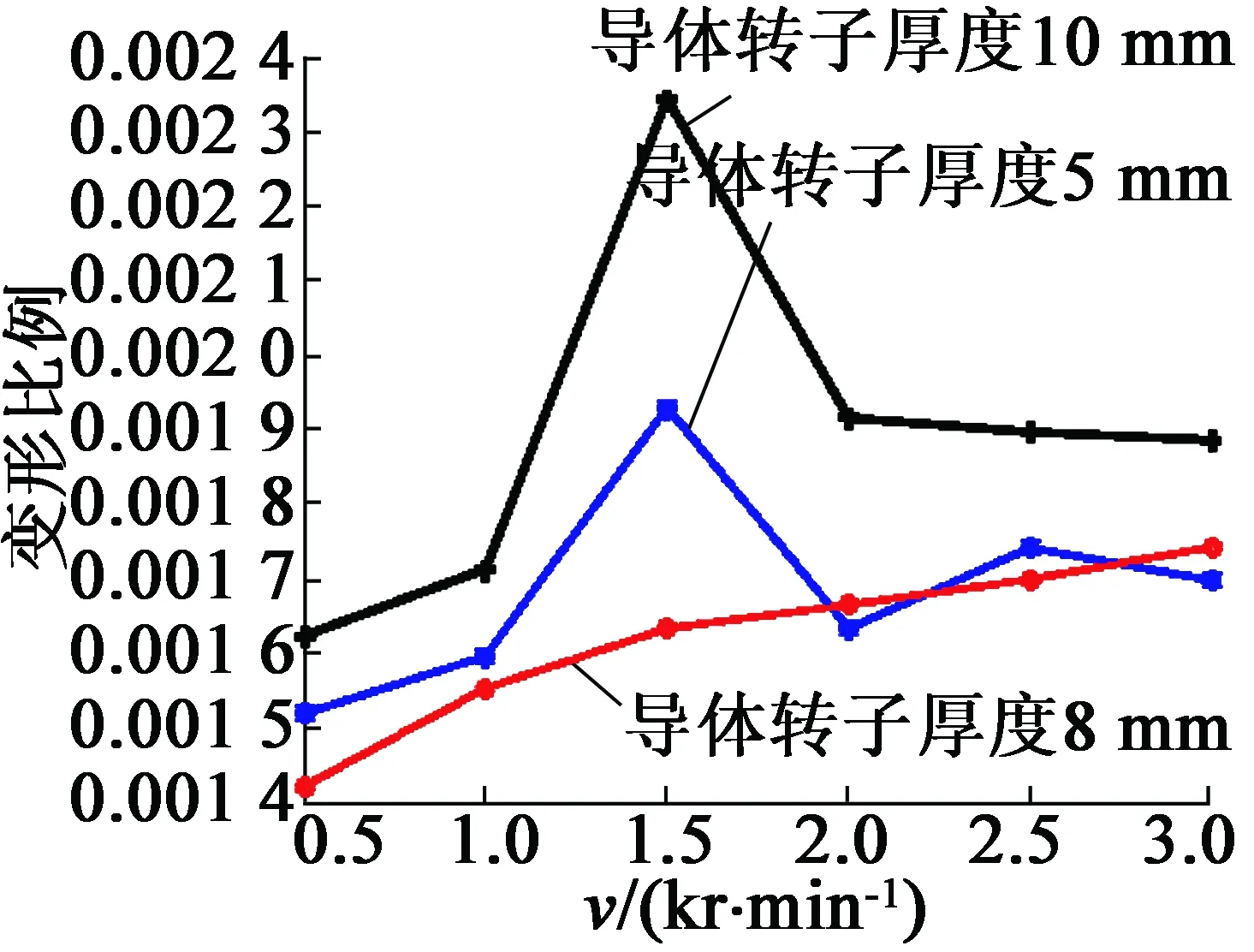
(b) 推进面积为2/3

(c) 推进面积为3/3
通过对图6进行分析,初步可以得到结论如下:不同厚度的导体转子在不同推进位置随着转速的增加,振动逐渐增大到达最大值后逐渐减小。相同转速下,当导体转子推进位置为2/3时,导体转子的振动情况最差。在相同推进位置处,转速在1 500 r/min左右,不同厚度的导体转子振动情况最差。通过对比,导体转子厚度为8 mm时,导体转子整体振动效果最优。
4 实验分析
本文采用的振动测试实验平台如图7所示,包括异步电动机、混合式永磁调速器、振动采集系统。图7中设有2个测点,测点1位于混合式永磁调速器外壳上,测点2位于混合式永磁调速器负载轴上,其中测点2为备用测点。

图7 混合式永磁调速器振动实验
测量混合式永磁调速器振动时,首先起动异步电动机,调节混合式永磁调速器气隙,将负载轴调至预定转速。随后控制电涡流制动器,增大负载轴转速,记录混合式永磁调速器振动数据,对其进行时域、时频域分析。最后得到时域波形如图8所示。
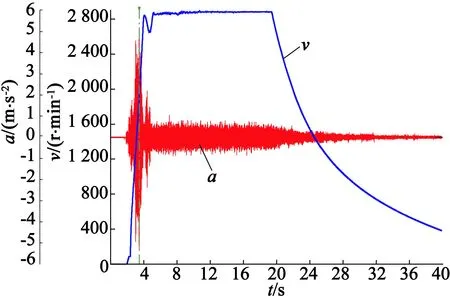
图8 振动时域波形图
实验验证了混合式永磁调速器轴向导体转子与径向导体转子为厚度8 mm时,混合式永磁调速器的振动最小。
5 结 语
本文研究了混合式永磁耦合调速器中径向导体转子对轴向导体转子振动问题。研究了不同厚度的径向导体转子对导体转子的影响,利用有限元软件仿真分析与实验验证。得到导体转子厚度为8 mm时,混合式永磁调速器整体振动最小。为混合式永磁调速器振动研究提供一定的理论依据。
