V型内置式永磁同步电动机齿槽转矩削弱方法研究

周 建，钱 喆，王群京，李国丽，陈 鑫，姜 鸿

(1.安徽大学 高节能电机及控制技术国家地方联合实验室，合肥 230000；2.安徽中磁高科有限公司，安庆 246000)

0 引 言

与感应电机相比，永磁同步电动机的结构更紧凑，体积更小，质量更轻，并且具备可靠性高和损耗低等优点；同时，由于永磁同步电动机具有较高的功率密度和转矩密度以及较宽的调速范围，作为驱动电机，其在新能源汽车中得到了广泛的应用。齿槽转矩是永磁同步电动机中一个重要的性能指标，因此对其进行深入的研究分析是十分必要的。同时，采取适当的方法来减小齿槽转矩，有利于提升永磁同步电动机的整体性能。

近几年，国内外学者对永磁同步电动机的齿槽转矩及其削弱方法进行了一系列研究。文献[1]提出从优化极槽配合、添加辅助齿或辅助槽以及改变定子槽开口大小等方法来削弱齿槽转矩。文献[2]基于内置式永磁同步电动机，提出可通过转子分段斜极来削弱齿槽转矩，并给出了理想的分段数、分段长度以及分段磁极的偏转角度。文献[3]研究了4极12槽、4极15槽和4极18槽电机的齿槽转矩，提出与整数槽相比，选择分数槽电机会产生更低的齿槽转矩。文献[4]在永磁同步电动机定子齿端部采用了一种“健壮设计”以削弱齿槽转矩。文献[5]运用傅里叶级数的分析方法，提出了一种基于槽口偏移削弱齿槽转矩的方法。文献[6]提出，运用开辅助槽的办法，电机齿槽转矩的幅值有明显降低，并且还进一步探究了所开辅助槽的深度以及辅助槽中心线夹角的大小与电机齿槽转矩的关系。经过实际验证，上述方法均可较为理想地削弱齿槽转矩。

上述方法大多是从内置式永磁同步电动机定子的角度出发，在优化齿槽转矩的同时，需要对电机的定子做较大修整，容易对电机的其他性能造成较大影响。而本文提出的方法是对电机的转子进行适当的修形。

本文首先建立数学分析模型，给出了基于转子参数的V型内置式永磁同步电动机极弧系数的数学表达式，然后利用能量法给出齿槽转矩关于极弧系数的数学解析式，提出对于不同极数和槽数的永磁同步电动机，总存在一个最优的极弧系数值。通过转子修形使电机极弧系数达到理论最优值，以削弱齿槽转矩。最后以一台8极48槽的V型内置式永磁同步电动机为例，进行了有限元仿真验证。

1 数学模型的建立

1.1 极弧系数的数学模型

永磁同步电动机的极弧系数定义为电机永磁体所跨的弧长与极距的比值。由于两个弧在同一个圆上，故弧长的比值等于弧长所对应圆心角的比值。在式(1)中，αPole为电机一极对应的电角度，αPM为一极永磁体所对应的电角度，极弧系数αp可表示为αPM与αPole的比值。

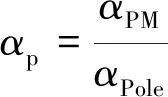
(1)

如图1所示的电机转子模型中，两块永磁体均采用平行充磁，并成V字型结构。D为一个极下相邻永磁体的最小距离，β为磁钢圆心角，w为一个极下永磁体的长度总和，r为转子圆心到磁钢的最大距离，φ为一极永磁体所对应的机械角度。

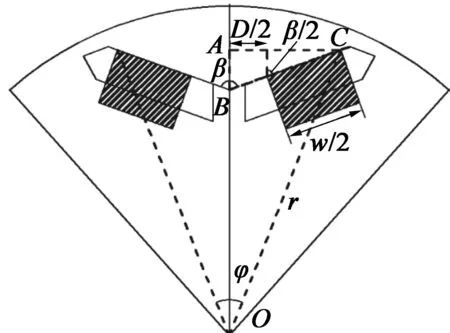
图1 电机转子参数化分析模型

在△ABC和△OAC中，由正弦定理可得：

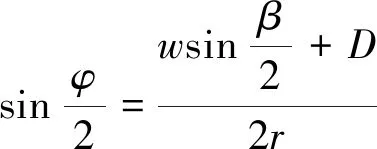
(2)

则一极永磁体对应的机械角度：

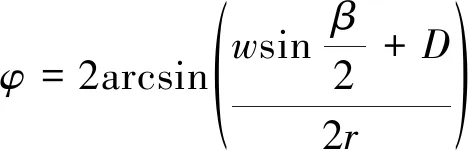
(3)

电机极弧系数：

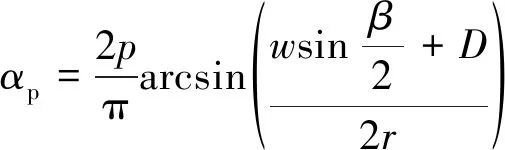
(4)

式中:p为电机极对数。通过转子修形改变式(4)中的磁极参数，可以改变电机的极弧系数值。

1.2 齿槽转矩的数学解析式

永磁同步电动机定子绕组不通电时，电机的齿槽转矩可由式(5)计算所得。其中，W是电机的内部磁共能，α是电机定转子的相对位置角。

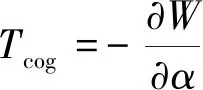
(5)

而电机内部的磁共能W可近似表示：

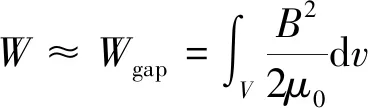
(6)

忽略饱和、漏磁的影响，则永磁同步电动机气隙磁密可表示：

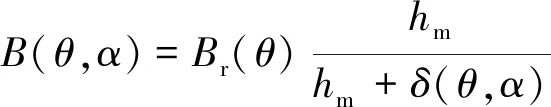
(7)

式中：Br(θ)是永磁体的剩余磁通密度；hm是永磁体的宽度；δ(θ,α)是电机气隙的有效长度。

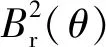
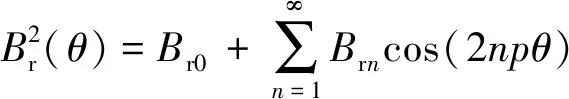
(8)

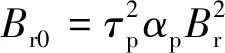
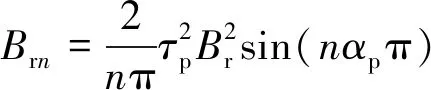
式中：τp是每极永磁体总长度与每极极弧长度的比值；αp为电机的极弧系数；Br是永磁体剩磁。

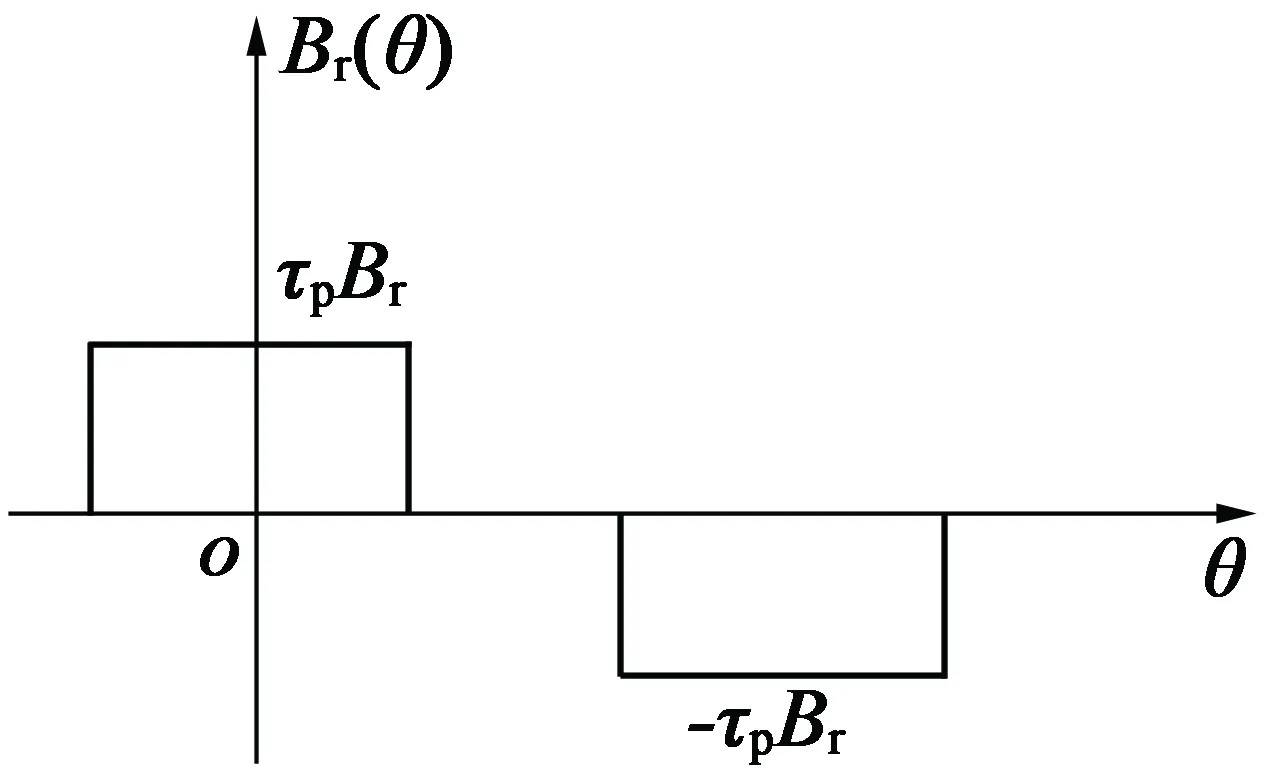
图2 沿圆周方向的分布

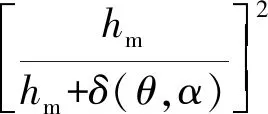
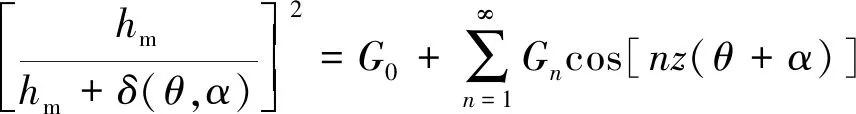
(11)

由式(6)～式(11)，可得：

将式(12)对相对位置角α求负导数，可得永磁同步电动机齿槽转矩解析式：

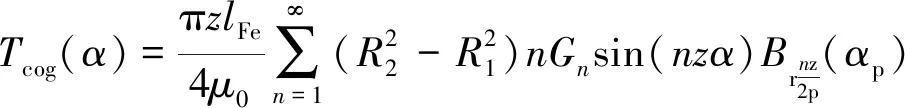
(13)

式中：z是定子槽数；lFe是电机电枢铁心的轴向长度；n是使nz/(2p)为整数的整数。

2 理论最优极弧系数

结合这两个结论，可得对于不同极槽配合的永磁同步电动机，要使齿槽转矩最小，电机理想的极弧系数αp：

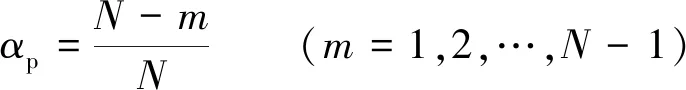
(14)

式中：N=Nc/(2p),Nc是z和2p的最小公倍数。

但需要注意的是，尽管理想的αp值有多个，但如果αp的值太小，虽然齿槽转矩减小了，但是永磁体的宽度也会变得很小，而不能提供足够的磁通，因此，通过优化极弧系数减少齿槽转矩时应尽量选取数值较大的αp[7]。由此可知，对于不同极槽配合的永磁同步电动机，理论上最优的极弧系数值：

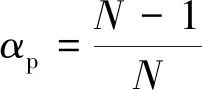
(15)

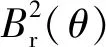
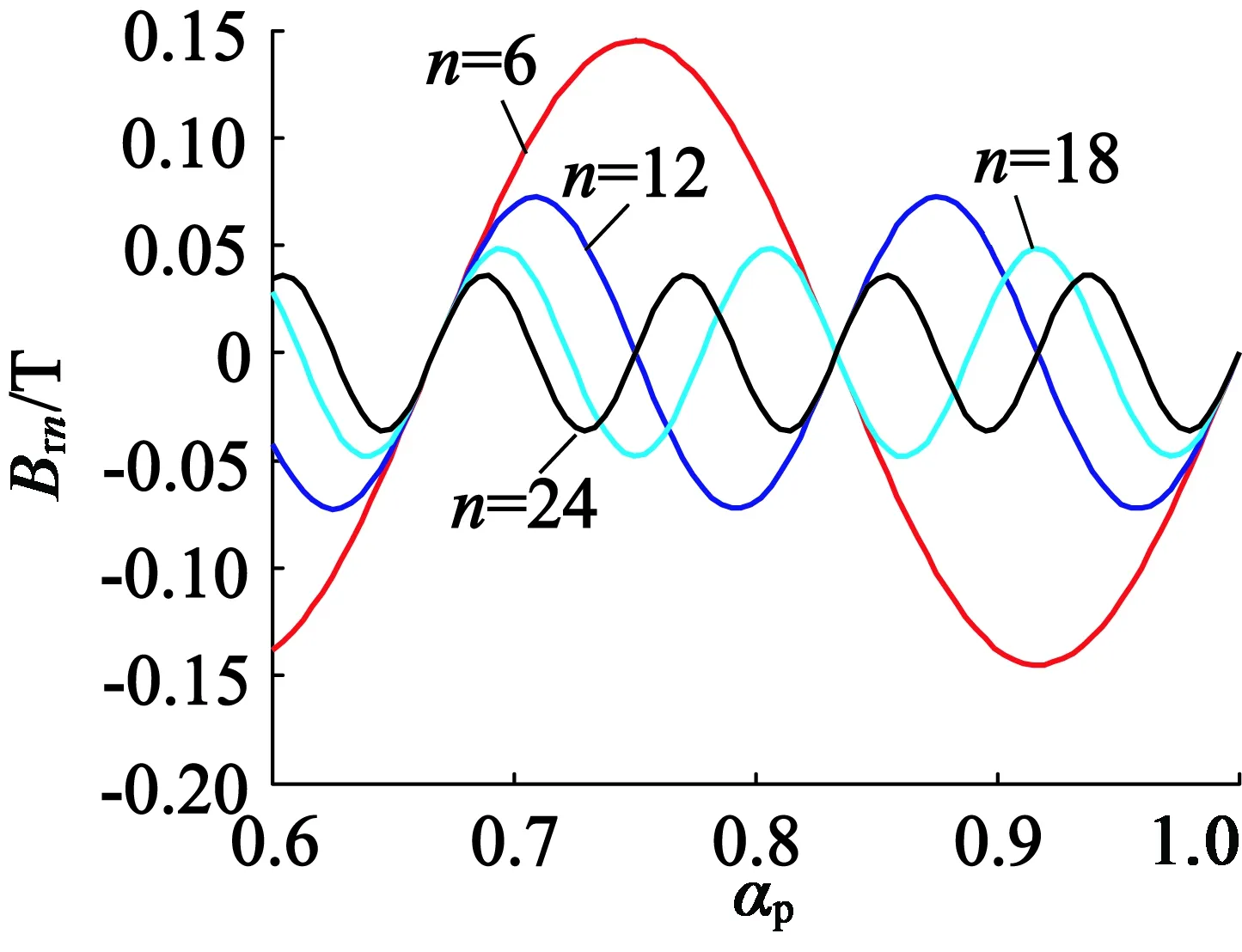
图3 Brn随极弧系数的变化曲线

3 转子极弧系数优化

本文采用8极48槽V型内置式永磁同步电动机，其主要参数如表1所示。

表1 内置式永磁同步电动机的主要参数

由式(4)可得此时电机的极弧系数αp=0.796 1，并未达到理论最优值αp=0.833 3。

采用转子修形的方法优化极弧系数，为了最大程度地减小对电机性能的影响，选择修改的参数：相邻永磁体最小距离D和相邻永磁体磁桥距离Rib，其余参数不变。随着参数D和Rib的变化，电机极弧系数αp的数值如表2所示。

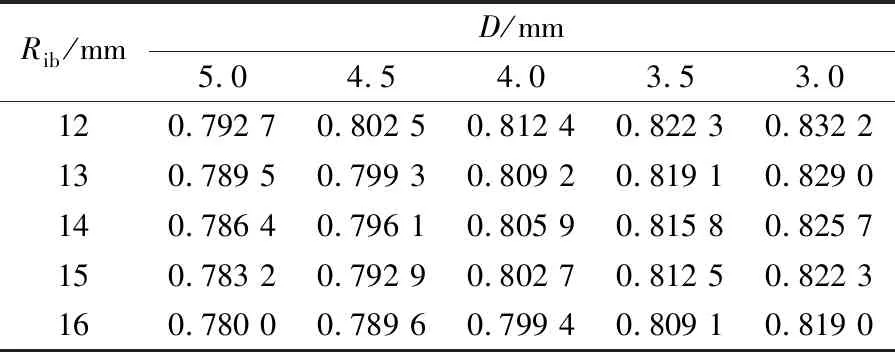
表2 随参数变化的电机极弧系数值

当D=3 mm，Rib=12 mm时，电机的极弧系数αp=0.832 2。考虑到电机定子开槽导致的漏磁而产生的误差影响，可以认为在这个修形方案下，极弧系数已经达到了最优。这表明，采用转子修形的方法可以优化电机的极弧系数，使其趋于理论最优值，为削弱电机齿槽转矩提供了途径。

4 电机模型仿真验证

为验证本文方法的有效性，以电机转子修形前αp=0.796 1和电机转子修形后αp=0.819 1、αp=0.832 2这三种情况为例，对电机空载性能和负载性能等两方面进行分析比较。

利用有限元分析软件建立电机模型，电机极数为8，为减少所仿真电机的尺寸，节省时间。可以只对电机的八分之一模型进行仿真研究，如图4所示。

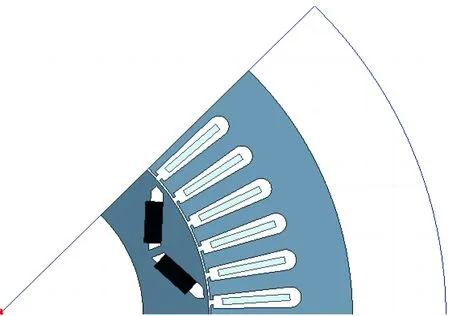
图4 电机仿真模型

4.1 空载气隙磁密分析

转子修形前后电机空载气隙磁密一个周期下的波形如图5所示。可以看到，转子修形后，对电机空载气隙磁密影响整体较小。

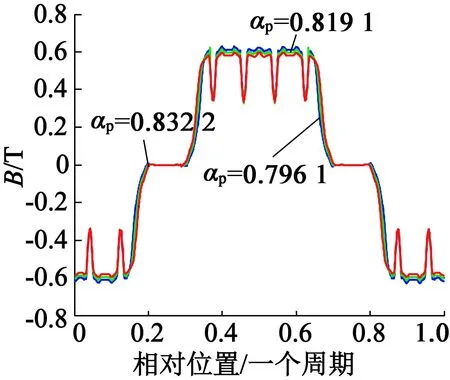
图5 空载气隙磁密波形

在对空载气隙磁密作傅里叶分析后，结果如表3所示。

显然，随着极弧系数进一步趋于理论最优值，气隙磁密的基波幅值略有下降。这主要是因为修形后，转子磁钢夹角增大，削弱了V型永磁体结构的聚磁效应。不过，可以看到，当转子修形后极弧系数取最优值时，气隙磁密的谐波含量有所降低，这有利于降低齿槽转矩。

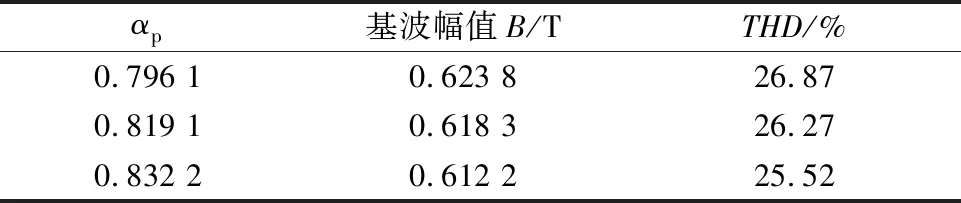
表3 空载气隙磁密傅里叶分析结果

4.2 齿槽转矩分析

不同极弧系数下，电机齿槽转矩波形如图6所示。由图6可知，当电机极弧系数αp分别为0.7961，0.819 1和0.832 2时，电机的齿槽转矩变化趋势相同。修形前，αp的值为0.796 1，电机齿槽转矩的峰值为1.783 0 N·m；修形后，当电机极弧系数为0.819 1，未达到最优值时，齿槽转矩的峰值也略有下降，为1.232 4 N·m。而当极弧系数为最优值时，齿槽转矩的峰值为0.298 9 N·m。与修形前相比，齿槽转矩峰值下降了约82.13%。这表明，通过优化永磁同步电动机的极弧系数，能有效减小电机的齿槽转矩，并且当极弧系数取到最优值时，削弱效果最为显著。

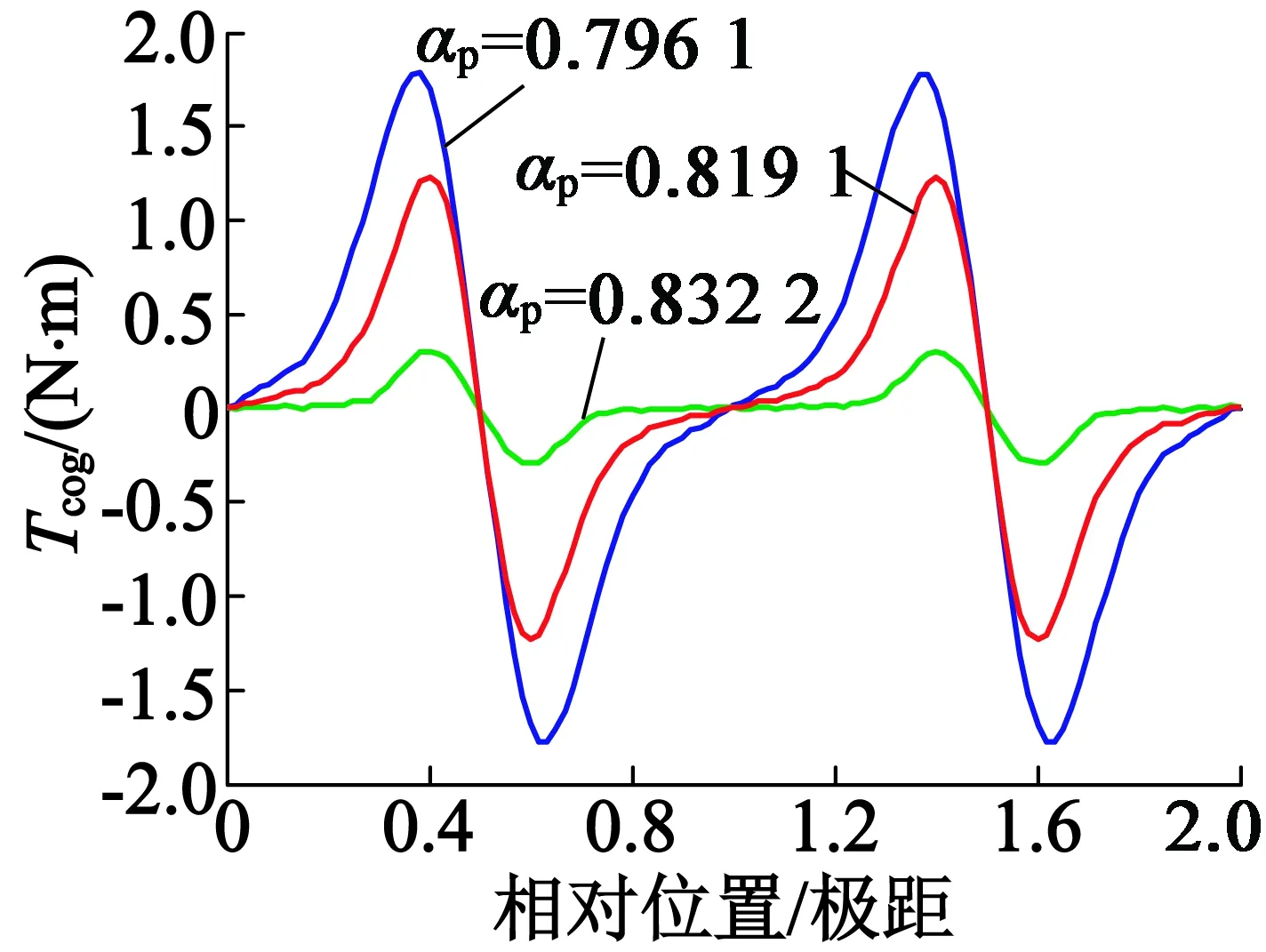
图6 电机齿槽转矩波形

4.3 负载性能分析

电机在不同极弧系数下一个极距内的输出转矩波形如图7所示。

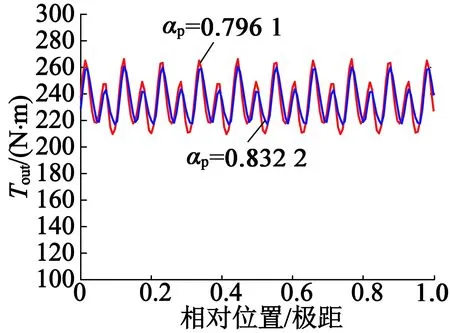
图7 电机输出转矩波形

结合图7，可以将电机在不同极弧系数下与输出转矩有关的数值列表，如表4所示。

由表4可知，通过转子修形，在最优极弧系数时，电机的最大输出转矩下降了约2.2%，输出转矩的最小值和平均值反而略有上升。这对于电机的整体输出性能而言影响不大。而电机的转矩脉动降低了4.38%，有利于提升电机的振动和噪声性能。

表4 电机输出转矩参数

5 结 语

本文首先研究了永磁同步电动机极弧系数对电机齿槽转矩的影响，给出了一种确定电机最优极弧系数的方法；同时提出了通过参数化扫描的方式，确定理想的转子修形方案，使电机极弧系数达到理论最优值，可以很好地降低电机的齿槽转矩。有限元分析结果表明，在对电机整体输出性能影响不大的前提下，采用优化电机极弧系数的方法，可以降低齿槽转矩，并且在最优极弧系数时，削弱效果最为明显，从而验证了本文方法的有效性。