基于改进干扰观测器的稳定平台扰动抑制技术

2019-08-01丁祝顺蒋鸿翔来新晓

导航与控制 2019年3期

丁祝顺，李洁，蒋鸿翔，来新晓

（1.北京航天控制仪器研究所,北京100039；2.国防科技大学,长沙410073）

0 引言

航空遥感主要被应用于资源勘查、地理测绘等领域，用于获取高分辨率的遥感数据。由于在飞行过程中受到大气湍流、突风等因素的影响，载机难以保持自身姿态的平稳，使得遥感相机的视轴低频晃动，成像质量下降。同时，载机发动机的高频振动使得遥感相机的成像质量进一步降低[1]。作为航空遥感系统的重要组成部分，稳定平台采用被动或主动隔振的方式滤除发动机的高频振动。利用机/电伺服控制方案隔离载机的低频角运动，以及隔离稳定平台自身由装配等原因带来的不平衡扰动和摩擦等扰动，可使相机视轴始终保持垂直指向[2-4]。

稳定平台的伺服控制精度决定了相机的视轴稳定性，因此，研究平台的扰动抑制方法具有重要的意义。经典的PID控制方法采用了速度环/位置环的双环控制方案，可以抑制扰动的影响。但是，由于受限于陀螺及位置姿态系统等传感器本身的精度，伺服控制的精度往往难以满足要求。本文在对不平衡扰动、摩擦和基座角运动等扰动进行分析的基础上，设计了一种改进干扰观测器的控制策略。通过观测，得到稳定平台的各种扰动，将其反馈到控制端，最终实现对扰动的抑制。相比经典控制方法，控制精度提高了2～3倍。

1 稳定平台简介

如图1所示，稳定平台由外至内依次为横滚框、俯仰框和方位框，遥感相机与位置姿态系统（POS）被安装在最内框。作为稳定平台控制回路的传感器件，POS敏感平台的姿态信息，并通过数字伺服控制器驱动电机转动，保持视轴的指向。

图1 稳定平台原理框图Fig.1 Principle block diagram of stabilized platform

稳定平台控制系统采用双环控制：内环为速度环，能够使稳定平台保持惯性稳定；外环为位置环，能使稳定平台跟踪地理水平。稳定平台的控制框图如图2所示。

图2 稳定平台控制框图Fig.2 Control block diagram of stabilized platform

在图2中，1/（Ls+R）为电机模型，Ki为电机力矩系数，N为齿轮传动比，J为稳定平台转动惯量，Kg为陀螺标度因数，KA为惯组标度因数，Gs（s）为速度环控制器，GA（s）为位置环控制器，M为稳定平台的干扰力矩。干扰力矩的存在会使稳定平台的指向精度及视轴稳定精度变差，因此需要对其进行分析。

2 稳定平台干扰分析

由于机械结构设计和加工精度的影响，稳定平台框架的质心与几何中心偏离，产生不平衡力臂，进而在重力加速度和载体运动干扰加速度的共同作用下产生不平衡力矩[5]。不平衡力矩可以表示为

在式（1）中，m为稳定平台的质量，g为重力加速度，a为干扰加速度，f为干扰加速度的频率，l为不平衡力臂。

作为承载惯性稳定平台的基座，飞行载体在飞行过程中会受到大气湍流等外界扰动因素的影响，使得载体发生运动。对于惯性稳定平台而言，这便产生了基座角运动。由于基座角运动是由飞行载体受到各种内外扰动因素作用而形成的，其作用形式是多样的，在分析过程中可将其看作典型的正弦形式的扰动，故其可表示为

在式（2）中，A为基座角运动幅值，ω为基座角运动频率。

摩擦广泛存在于惯性稳定平台系统中，会使平台在低速运行时产生不平稳现象。Stribeck模型可以描述惯性稳定平台系统中存在的静摩擦、动摩擦及低速运动时摩擦随速度增加而减小的性质。因此，采用Stribeck模型来描述惯性稳定平台系统中存在的摩擦现象[6]。Stribeck摩擦模型可以表示为

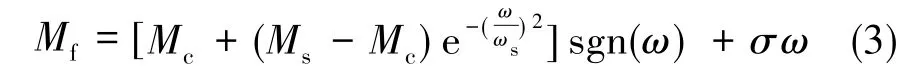
在式（3）中，Mc为库伦摩擦力矩，Ms为最大静摩擦力矩，ω为接触面之间的相对角速度，σ为粘性摩擦系数，ωs为Stribeck速度。

3 改进干扰观测器

干扰观测器（Disturbance Observer，DOB）可以将由外界扰动而引起的被控对象的输出与标称模型的输出之间产生的差异输入到控制输入端，并将其与实际的外界扰动做差，实现对扰动的完全抑制[7-8]。干扰观测器的原理图如图3所示。

在图3 中，Q（s）为低通滤波器，G0（s）为被控对象传递函数，为被控对象标称模型的逆，由图3可得

将Q（s）设计为低通滤波器，故在低频段Q（s）≈1时，系统可以实现对频率较低的外界扰动的抑制；而在高频段Q（s）≈0时，系统能抑制测量噪声的影响。

图3 干扰观测器的原理图Fig.3 Schematic diagram of disturbance observer

低通滤波器Q（s）的具体表达形式为

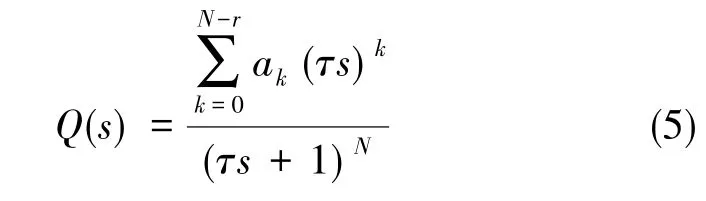
根据图1可得，被控对象为

将干扰观测器代入到惯性稳定平台系统中，可以表示为如图4所示的形式。

加入干扰观测器可以观测出系统中的扰动，将观测出的扰动加到控制端，可以实现对扰动和测量噪声的抑制。但是，被控对象的传递函数一般为真有理分式，这使得其标称模型的逆中包含微分环节，在物理上难以实现，因此需要对其进行改进。从图4中可以看出

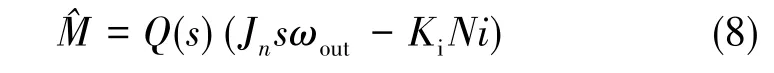
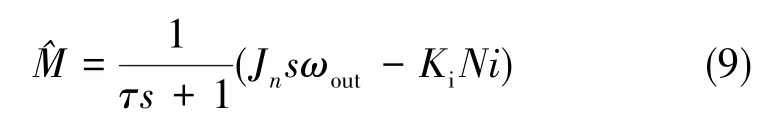
图4 带有干扰观测器的惯性稳定平台框图Fig.4 Diagram of inertial stabilized platform with disturbance observer

从式（9）可以看出，干扰观测器包含一阶微分环节，会导致系统对高阶量测噪声敏感。因此，可以对式（9）进行如下变化，避免出现微分环节

这样，改进后的干扰观测器如图5所示。

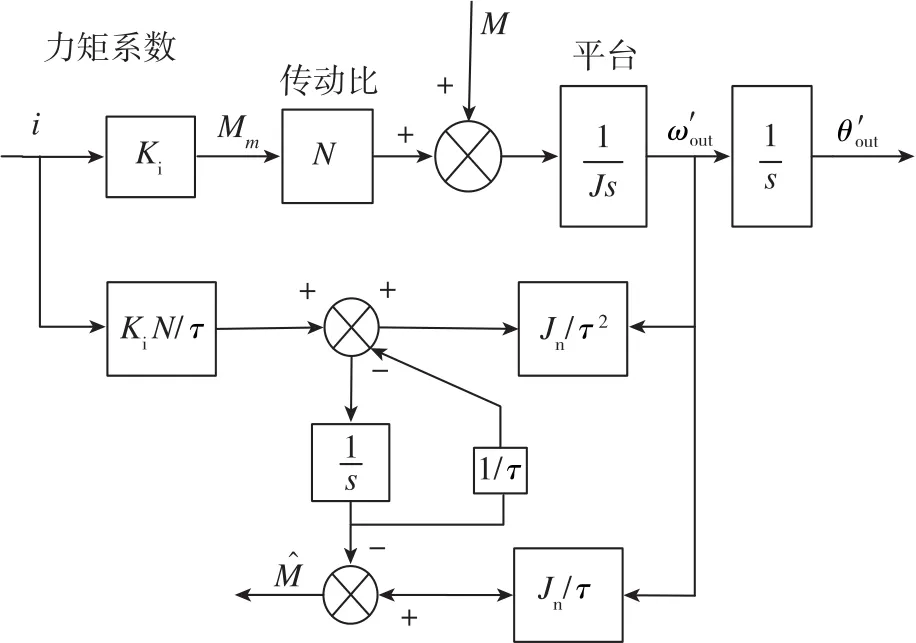
图5 带有改进干扰观测器的惯性稳定平台框图Fig.5 Diagram of inertial stabilized platform with improved disturbance observer

4 仿真与分析

稳定平台的仿真参数如下：电机电枢电阻为8.6Ω，电机力矩系数为0.25Nm/A，减速比为90，稳定平台转动惯量为2.767kg·m2，陀螺标度因子为1.2×106LSB/（rad/s），低通滤波器的滤波时间常数为0.002s。

稳定平台的质量为75kg，设偏心距为1cm，载体运动干扰加速度的幅值为1g，则不平衡扰动的表达式为Mmass=7.35+7.35sin2πft。

稳定平台允许的最大角速度幅值为20（°）/s，本文将基座角运动的幅值取为平台运动最为剧烈的情况，基座角运动的表达式为ωb=20sin2πft。

当不平衡扰动的干扰角速度频率和基座角运动频率均为1Hz时，在PID控制与改进干扰观测器的控制下，稳定平台的角度输出如图6所示。当不平衡扰动的干扰角速度频率和基座角运动频率均为2Hz时，在PID控制与改进干扰观测器的控制下，稳定平台的角度输出如图7所示。

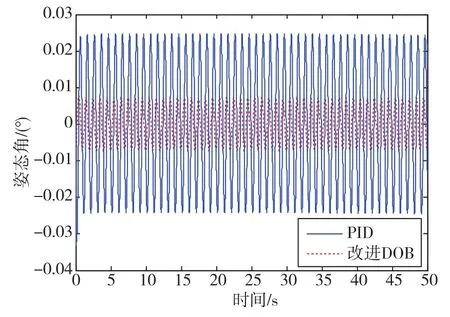
图6 扰动频率为1Hz时，PID控制与干扰观测器的控制效果Fig.6 Effect of PID control and disturbance observer control when frequency of disturbance is 1Hz

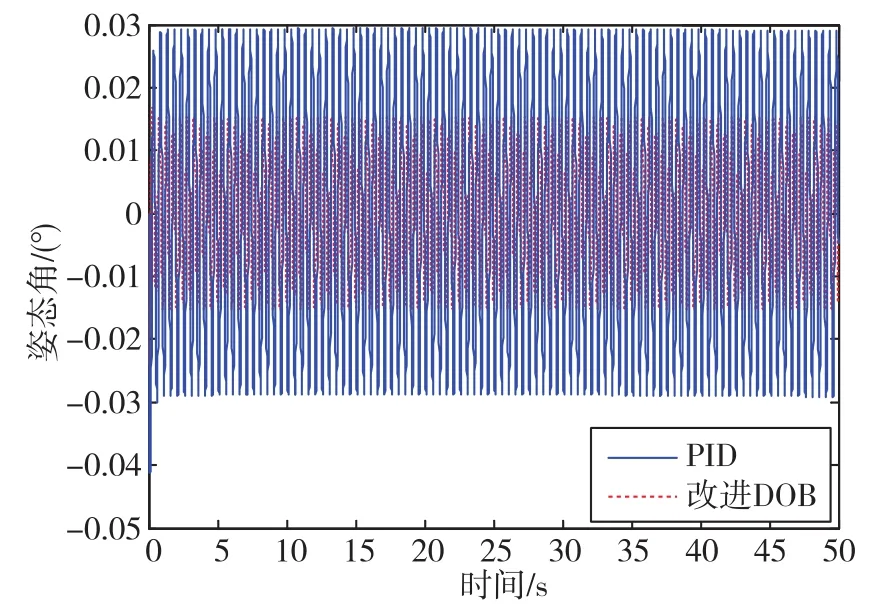
图7 扰动频率为2Hz时，PID控制与干扰观测器控制效果Fig.7 Effect of PID control and disturbance observer control when frequency of disturbance is 2Hz

从图6可以看出，当扰动频率为1Hz时，PID控制下稳定平台输出的角度峰值为0.024°。在加入改进干扰观测器之后，稳定平台角度输出峰值约为0.008°，提高了3倍。从图7可以看出，当扰动频率为2Hz时，PID控制下稳定平台输出的角度峰值为0.03°。在加入改进干扰观测器之后，稳定平台角度输出峰值约为0.015°，提高了2倍。仿真结果表明，在不同的扰动作用下，改进干扰观测器的扰动抑制效果均优于PID控制，大大提升了稳定平台的稳定效果。