绝对重力仪隔振系统发展综述

要佳敏，伍 康

（1.清华大学精密测试技术及仪器国家重点实验室,北京100084；2.清华大学精密仪器系,北京100084）

0 引言

绝对重力测量是指对重力加速度绝对值的测量。重力是作用在地球表面某一质点的地球万有引力与自转离心力的合力，垂直于该质点所在位置的大地水准面。地球表面各点的万有引力和离心力都随测量点的时空坐标的改变而变化。因此，重力加速度绝对值是一个随时间和空间变化的重力场参数。

重力加速度绝对值一般用g表示，约等于9.8m/s2。在重力测量领域，更常用的单位是伽（Gal，1Gal=0.01m/s2）。目前，重力加速度值测量结果的单位普遍为毫伽（mGal）和微伽（μGal）。 绝对重力测量在计量学、地球物理、资源勘探、辅助导航、军事、海洋监测等领域中有着重要意义和广泛应用。

绝对重力测量最早可以追溯到1590年意大利物理学家伽利略进行的比萨斜塔实验，至今依次出现了摆法、自由落体法和原子干涉法这3种主要的测量方法。1672年，法国天文学家Richer发现摆的振荡周期与其所处纬度有关。1792年，法国的Borda和Cassini用线摆较为精确地测量了重力。此后，摆仪成为了主要的绝对重力测量仪器。其中，又出现了更为复杂的复摆和可倒摆[1]，并在可倒摆仪的基础上建立了被广泛使用的 “波茨坦重力系统[2]”。

进入20世纪后，自由落体法出现并不断发展，实现了更高的测量精度，逐渐取代了摆法而成为了主要的绝对重力测量方法。早期，苏联的Agaletzkij等[3]、加拿大的Preston-Thomas等[4]、法国的Thulin等[5]及美国的Faller等[6]均开始研究基于自由下落的绝对重力仪。1967年，英国的Cook研发了一种上抛下落式的绝对重力仪[7]，该重力仪使用固定位置的光学狭缝和光脉冲触发电子计时器装置来获取落体轨迹的 “时间位移对”信息，并由此计算出重力加速度。此后，随着时间测量、位移测量和信号采集技术的不断发展，绝对重力仪广泛采用激光干涉仪和原子钟来获取自由落体轨迹的 “时间位移对”，并配备了隔振系统。通过拟合成百上千对的时间位移测量值来求解重力加速度的绝对值，大大提升了测量精度。20世纪80年代，在修正固体潮汐之后，该类型仪器的测量精度已普遍达到了±10μGal。其中，最著名且应用最为广泛的当属美国Micro-g LaCoste公司在JILA型绝对重力仪[8]的基础上研制的FG5型和FG5X型绝对重力仪[9-10]，如图1所示。该仪器属于自由落体式，配备了其团队自主研发的Superspring隔振系统[11]，测量精度达到了微伽量级。此外，法国乔治S.A.公司制造的GA60型上抛下落式绝对重力仪是第一台可移式商用绝对重力仪[12]。目前，精度最高的同类型仪器是意大利计量院研制的IMGC-02型绝对重力仪，其曾长期监测意大利的火山活动[13]。

图1 Micro-g LaCoste公司的FG5X型绝对重力仪Fig.1 FG5X absolute gravimeter developed by Micro-g LaCoste

中国计量科学研究院于1975年研制出了我国第一台遵循自由落体法的固定式绝对重力仪，其测量精度在百微伽量级，并在此基础上研制出了我国第一代可移式绝对重力仪（NIM-I型），其测量不确定度为20μGal。1983年，中国计量科学研究院研制并逐渐完善了其第二代绝对重力仪（NIM-II型），并参加了多次国际重力比对[14]。中国计量科学研究院-清华大学精密测量联合实验室于2012年研制完成了T-1型高精度绝对重力仪[15]。该重力仪参加过2011年欧洲绝对重力仪比对，参加过2013年与2017年的国际绝对重力仪比对，其比对结果与参考值符合。

20世纪90年代，美国的Kasevich与Chu首次成功使用原子干涉法测量了重力加速度[16]，此后成熟的原子干涉式绝对重力仪出现。其基本原理为：原子团在自由下落的过程中经过三次Raman跃迁，形成原子干涉，其相位与重力加速度和有效波矢成正比，与Raman脉冲时间间隔的二次方成反比，可由此计算出重力加速度的绝对值。相比经典自由落体式绝对重力仪，原子干涉式绝对重力仪具有更快的测量频率和更小的反弹效应。但是，其发展起步较晚，与FG5型绝对重力仪相比，目前在性能方面仍存在差距。法国巴黎天文台（LNESYRTE）研制的CAG-01型原子重力仪已参加过多次国际重力比对[17]，已由MUQUANS公司进行了商业推广。

典型的自由落体式绝对重力仪以激光波长为长度基准，以原子钟为时间基准，采用激光干涉仪测量下落物体在真空中自由下落的轨迹，以获得大量的 “时间位移对”数据。高速数据采集卡采集这些数据并将其传输到信号处理系统中，经过二次拟合求解出重力加速度。这种绝对重力仪的基本结构如图2所示，其主要由自由落体装置、激光干涉测量装置和振动处理装置组成。其中，重力仪包含的主要部件有：1）下落物体。其内部固定角锥棱镜，以保证可以用干涉法测量其在真空腔中的自由下落轨迹[18]；2）电机及传动结构。用于控制下落物体的释放和进行重复测量；3）激光干涉仪中的光电探测器。可以将干涉条纹信号转变为电信号；4）参考角锥棱镜。用于为干涉测量提供稳定的参考点，理论上其应相对惯性参考系静止。参考棱镜如果被放置于地面，必然会受到地面振动的影响，使得振动噪声耦合进干涉仪测量到的落体运动轨迹中，严重影响重力加速度值的测量精度，因此必须对其进行相应的处理。

图2 自由落体式绝对重力仪的组成Fig.2 Formation of free-fall absolute gravimeter

1 地面振动噪声对绝对重力测量的影响

地面振动噪声对绝对重力测量的影响随测量地点的改变而有较大区别，波动范围从百微伽量级到十毫伽量级。对测量精度达到微伽量级的绝对重力仪而言，这是一项必须被处理的影响因素。地面振动包含水平分量和竖直分量。由于绝对重力测量只选取竖直方向的运动数据进行计算，前者造成的参考棱镜水平运动不会影响测量，因此计算过程只需考虑竖直方向上的振动噪声。

影响绝对重力测量的地面振动主要可分为两种，一是环境噪声，二是仪器噪声。

首先是环境噪声，它与测量时间和测量点的坐标、地基及周围环境有关。环境噪声的来源一般可以通过频率进行区分：一是人类活动的噪声，一般大于1Hz，如车辆和风机等人工振源的振动（频率一般为1Hz～150Hz）、建筑物和树木的晃动（与土壤特性有关，频率一般为10Hz以上）及仪器测试期间附近的人员走动（频率一般为1Hz～3Hz）；二是地脉动噪声，一般在0.1Hz～1Hz，如风激振（频率一般为0.1Hz～2Hz）、地震和火山等地球内部运动引起的振动（频率一般为0.1Hz～30Hz）以及地脉动，主要包括海浪撞击海岸和海浪相互碰撞时在地壳中产生的表面波和体波；三是大气运动噪声，一般小于0.1Hz，如风造成的植物晃动及气压波动。

总体来看，可以选择在远离人类活动频繁区域的、偏僻安静的地点进行测量，以减少第一类环境噪声的影响；第三类环境噪声主要由气压波动导致，其对绝对重力测量的影响可以忽略[19]；只有来源于地球本身的第二类环境噪声无法避免，且对测量的影响也最大，需要对其进行进一步的分析。图3为2012年Trnkoczy等人测得的全球不同地点的地脉动噪声垂直分量功率谱密度[20]，其中的虚线为谱密度曲线的上下界，表示全球新高低噪声模型，由美国地质调查局的Perterson等人于1993年通过处理分布在全球的多个地震台站的数据而得，其分别被称为新高背景噪声模型（NHNM）和新低背景噪声模型（NLNM）[21]。 从图 3可以看出，地脉动噪声在周期为10s～20s和4s～6s的位置存在两个峰值，前者被称为第一类地脉动，与全球海浪的主要周期一致，一般被认为是浅海海岸被海浪压力驱动所产生的；后者被称为第二类地脉动，一般被认为是由近海岸两列方向相反、频率相同的第一类地脉动的非线性耦合导致的。

图3 地脉动噪声模型的加速度功率谱密度Fig.3 Acceleration power spectra of ambient seismic noise

地面振动噪声的第二大类是仪器噪声。在仪器测量期间，传动机构每次释放下落物体时，绝对重力仪的静态质量将瞬间减小，此时地面支持力与仪器所受重力的合力不再平衡，可等效为一个瞬时冲击；之后，传动机构每次承接下落物体时，二者之间的碰撞也会对地面产生冲击。由这两种情况造成的地面振动噪声的频率相对较高，仅在安静环境下会对绝对重力仪产生较为明显的影响。

目前，常用的解决地面振动噪声的方法包括两种。一是使用隔振系统，以尽可能减少地面振动对参考棱镜的影响。由前文对振动来源的分析可知，这种隔振系统主要在竖直方向上发挥作用，其本征频率应至少低于0.1Hz（以下简称为 “超低频垂直隔振系统”）；二是建立一套振动补偿方法，利用传感器测量参考棱镜的运动，在处理数据时对干涉仪测量到的落体轨迹数据进行修正。这两种方法在各种自由落体式和原子干涉式绝对重力仪中均有应用，不过到目前为止，大多数绝对重力仪仍然主要依靠超低频垂直隔振系统来实现高精度的测量。

2 超低频垂直隔振系统

相比水平隔振系统，垂直隔振系统必须在隔振的同时支撑被隔振物体的重量，因此其更为复杂，研发难度更大[22]。多年来，已有多家国内外机构针对本征频率低于0.1Hz（即本征周期大于10s）的超低频垂直隔振系统进行了研究，下文将进行详细介绍。

超低频垂直隔振系统从原理上可被分为被动式（无源）隔振和主动式（有源）隔振，其中主动式隔振又可被分为一级主动隔振和二级主动隔振。

2.1 被动式隔振系统

被动式隔振系统主要包括零长弹簧结构、几何反弹簧结构、欧拉压杆结构、扭杆弹簧结构等形式。从本质上而言，它们均是通过设计弹性元件的结构而使系统具有较低的本征频率。

1934年，LaCoste提出了最初用于研制长周期地震计的零长弹簧结构，如图4所示。后来，其也被应用于研制垂直隔振系统[23]。在图4（a）中，O为摆杆转轴，A和B分别为零长弹簧的上、下悬挂点，l1和l2分别为A、B到转轴O的距离，m为摆杆质量，l3为质心到转轴O的距离，θ0为AO相对于竖直线的偏角，θ为摆杆相对于水平线的偏角，h为转轴O相对于零长弹簧的距离。零长弹簧的拉力与弹簧总长成正比，即弹簧的等效原长为0。记弹簧的等效刚度为k，被隔振物体和摆杆的总质量为m。理论上，可以设计图4中的摆杆长度参数l2和l3，使得。此时，便可保证摆杆在任意位置均处于平衡状态，即对任何θ而言，系统的回复力均为0，本征周期趋于无穷大。但在实际系统中，由于弹簧受蠕变和温漂等因素的限制，系统的实际本征周期一般在15s～20s之间。

图4 基于LaCoste零长弹簧结构的长周期地震计Fig.4 Long-period seismometer based on LaCoste zero-length spring

基于长周期地震计的隔振系统一直被应用于IMGC系列的上抛下落式绝对重力仪中，如目前正在使用中的IMGC-02型绝对重力仪[24-25]，如图5所示。

图5 IMGC型重力仪的基本结构及IMGC-02型重力仪Fig.5 Basic structure of IMGC gravimeter and IMGC-02 gravimeter

清华大学的李刚等利用反馈控制对LaCoste零长弹簧的结构进行了改进，使用光学杠杆探测了摆杆的角位移，反馈电路根据探测到的位移信号控制音圈电机驱动摆杆，补偿弹簧由蠕变和温漂而被造成的影响。改进后的隔振系统如图6所示，其在实际工作时的本征周期达到了32s，可持续稳定工作1年以上[26]。

图6 李刚等提出的对基于LaCoste零长弹簧的垂直隔振系统的改进Fig.6 Improvement of vertical vibration isolation system based on LaCoste zero-length spring proposed by Li

目前，应用于绝对重力仪中的被动式隔振系统主要采用的都是这种零长弹簧结构。除此以外，还有另外几种被动式垂直隔振系统。

首先是在LIGO、Virgo等引力波探测器中广泛使用的几何负刚度弹簧（Geometric Anti Spring，GAS）结构[27-31]，如图 7（a）所示。 它由绕垂直轴对称分布的钢片组成，每根钢片的一端以角度θL固定在中心连接件上，另一端以角度θ0分别夹紧，负载与中心连接件固连。由于结构具有对称性，负载将只在垂直方向上运动[27]。该结构的等效物理模型为一个竖直方向上被拉伸的弹簧和数个在水平方向上轴对称分布的被压缩的弹簧[30]，在其平衡位置附近具有足够大的静态刚度和较小的动态等效刚度，相当于一个可以承受较大负载且具有长周期的线性垂直弹簧。Stochino等为改进型LIGO研制的振动衰减系统中的垂直隔振结构如图 7（b）所示[31]。

图7 几何负刚度弹簧隔振系统Fig.7 Vibration isolator based on geometric anti spring

欧拉压杆是另一种适合用于研制垂直隔振系统的结构。对于细长受压直杆来说，当其承受的轴向载荷小于使其屈曲的临界载荷时，杆只有轴向的压缩变形，没有侧向的弯曲变形；当轴向载荷稍大于使其屈曲的临界载荷时，压杆将失稳弯曲，并在此状态下处于新的平衡，成为欧拉压杆[32]。在这种轴向载荷处于临界载荷附近的独特状态下，载荷的微小变化会改变轴向变形，因此欧拉压杆可以等效为负长度弹簧。这种特殊力学特性使得欧拉压杆结构能够用来解决垂直低频隔振系统中负载弹簧静态变形过大的问题[32]，可以通过合理的结构设计使得系统在较为紧凑的空间内承受一定的重力，且具有很小的等效弹簧刚度。Winterflood等提出的基于欧拉压杆结构研制的实际隔振系统如图8所示[32]。

图8 Winterflood等提出的基于欧拉压杆设计的隔振系统Fig.8 Vibration isolator based on springs in Euler buckling mode proposed by Winterflood

此外，两个对称的扭杆弹簧系统的几何非线性效应可以在小范围内等效为具有长本征周期的垂直弹簧。Winterflood等之后也提出了基于这种结构的垂直隔振系统[33]，实际周期超过 20s，如图9（a）所示。在此基础上，赵鹏飞等提出了带附加质量的扭杆弹簧垂直隔振系统[34-36]，可以改善系统的高频隔振性能，如图9（b）所示。

图9 基于扭杆弹簧原理的隔振系统Fig.9 Vibration isolators based on torsion crank linkage

2.2 一级主动式隔振系统

一级主动式隔振系统可以简化为利用反馈控制实现长本征周期的一级弹簧振子模型，具体的实现方式为：利用加速度计测量被隔振物体的绝对加速度，反馈控制电路根据该信号控制直线电机驱动被隔振物体，使加速度信号保持不变，从而消除地面振动噪声的影响。

1984年，Saulson等研制的隔振系统如图10（a）所示[37]，本征周期达到25s。系统中的摆杆可绕左侧转轴转动，其重力通过弹簧来平衡。摆杆上放置加速度计，下方为直线电机，可依据上述原理利用反馈控制来抑制摆杆的振动。

与之类似，Hensley等研制的垂直隔振系统如图10（b）所示[38]，本征周期达到 30s，已应用在Stanford大学的原子干涉式绝对重力仪中。系统内部的振子由垂直弹簧支撑，在空气轴承的限制下做严格的垂直运动。振子上安装加速度计，通过直线电机施加反馈力来抑制振子的振动。

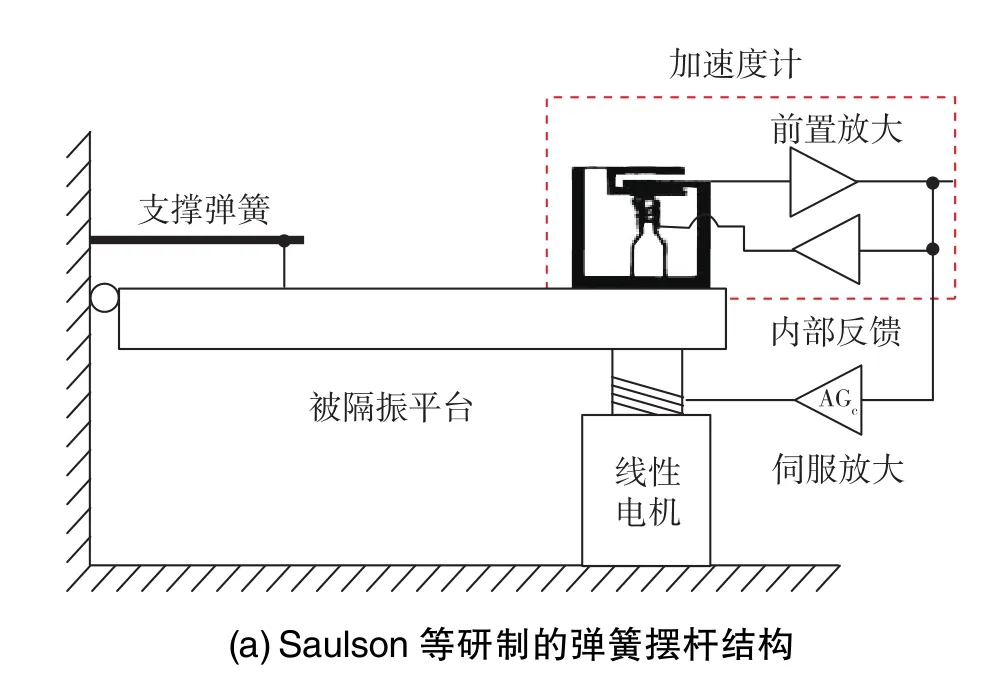
除了加速度计，也可以利用地震计作为测量被隔振物体运动的传感器。汤彪等基于Minus K Technology公司的被动隔振平台研制出的一级主动式隔振系统即采用这种方法[39]，如图10（c）所示，其本征频率达到66s。周敏康等用类似结构实现的三轴主动隔振系统在垂直方向上的本征周期可以达到100s[40]。

2.3 二级主动式隔振系统

二级主动式隔振系统可以简化为利用反馈控制实现长本征周期的二级弹簧振子模型，其设计思路来源于对无限长垂直弹簧的分析，如图11（a）所示。其中，M为被隔振物体质量，L为弹簧总长，xm（t）为被隔振物体垂直运动位移，d为弹簧上一点到弹簧底部的距离，xc（t）为该点的垂直运动位移。垂直弹簧刚度为k，下端悬挂重物后，其总长拉伸至L。当重物上下振动的绝对位移为xm时，弹簧线圈也随之振动。对于线圈上到重物的距离为d的一点来说，其振动的绝对位移xc=xm（1-d/L）。假设弹簧总长L≫d，此时弹簧的本征周期非常大，且弹簧线圈上与重物距离为d的一点的位移与重物的位移满足xc≈xm。也就是说，理论上，对长度为d的一段弹簧来说，如果其上端位移xc与悬挂重物的下端位移xm保持一致，则这段弹簧相当于无穷长弹簧的底部，等效本征周期无穷大。在实际系统中，可以通过控制弹簧的上端位移尽可能地趋近其下端位移，来提高系统的本征周期。

目前，在自由落体式绝对重力仪中应用最广泛的Superspring就是基于这种设计思路研制的二级主动式垂直隔振系统[41]，本征周期为30s～60s。该系统由来自美国JILA实验室的Rinker等于1983年提出，其原理如图11（b）所示，已配合FG5型等绝对重力仪沿用至今，也多次单独应用于国内外多家研究机构自主研发的绝对重力仪中。在图11（b）中，M1、M2分别为一级框架和被隔振物体的质量，k1和β1分别为一级弹簧的刚度和阻尼，k2和β2分别为二级弹簧的刚度和阻尼，F（t）为反馈力，xi（t）、x1（t）和x2（t）分别为地面、 一级框架和被隔振物体的垂直运动位移。该系统的基座与地面固连，受地面振动位移xi（t）的影响；第一级弹簧将质量为M1的一级框架悬挂在基座内部，绝对位移为x1（t）；第二级弹簧将被隔振物体M2悬挂在一级框架内部，绝对位移为x2（t）。如图12所示[41-42]，安装在一级框架内的光电探测电路探测一级框架M1与被隔振物体M2之间的相对位移信号为 Δx（t）=x2（t）-x1（t），控制电路根据该相对信号输出驱动信号给音圈电机，使一级框架M1在电机施加的反馈力F（t）的驱动下跟踪被隔振物体M2的运动，保持相对位移Δx恒定。此时，第二级弹簧的上端位移x1和下端位移x2几乎完全相同，即系统实现了相当长的本征周期。该系统隔振效果很好，但必须添加水平约束结构来保证一级框架只沿竖直方向运动，因此系统结构较为复杂[42]。

图11 垂直隔振系统示意图Fig.11 Diagram of vertical vibration isolation

1991年，同样来自JILA实验室的Nelson提出了另一种二级主动式隔振系统[43]，如图13所示，其本征周期大于30s。该系统利用平行四连杆机构替代Superspring中的一级框架，当机构摆杆转动角度很小时，可以起到水平约束的作用，保证一级机构只有沿垂直方向运动的单一自由度。

我国关于二级主动式垂直隔振系统的研究起步较晚，主要有清华大学、中国科学院测量与地球物理研究所、地震局等。清华大学的伍康等研制的隔振系统与Nelson提出的隔振系统类似，但结构更为紧凑，而且针对二级框架位置进行了优化，减小了高频耦合振动，本征周期可达到30s，如图14所示[44]。

图12 二级主动式垂直隔振系统SuperspringFig.12 Two-stage active vibration isolator Superspring

图13 Nelson提出的隔振系统Fig.13 Vibration isolation proposed by Nelson

图14 伍康等提出的隔振系统Fig.14 Vibration isolation proposed by Wu

2016年，清华大学的王观等研制出一种基于弹簧摆杆结构的二级主动式隔振系统[45]，如图15所示，其工作原理与Superspring的工作原理非常类似。在图15中，M1、M2分别为上摆杆和下摆杆的质量，其他参数同图11（b）中一致。不同之处在于，该系统中的一级框架为图15上方的一级摆杆，被隔振物体则与图15下方的二级摆杆固连，这两级摆杆都可以绕各自左侧与基座固连的铰链转动。当二级摆杆偏转角度非常小时，被隔振物体相当于做垂直方向上的一维运动。由于这种结构不需要添加对一级框架水平运动的约束，因此相比弹簧振子结构，它的抗干扰性更强，尺寸更为紧凑，如图16所示。该系统本征周期可达到100s，且能配合绝对重力仪保证81h的连续正常工作[45]。

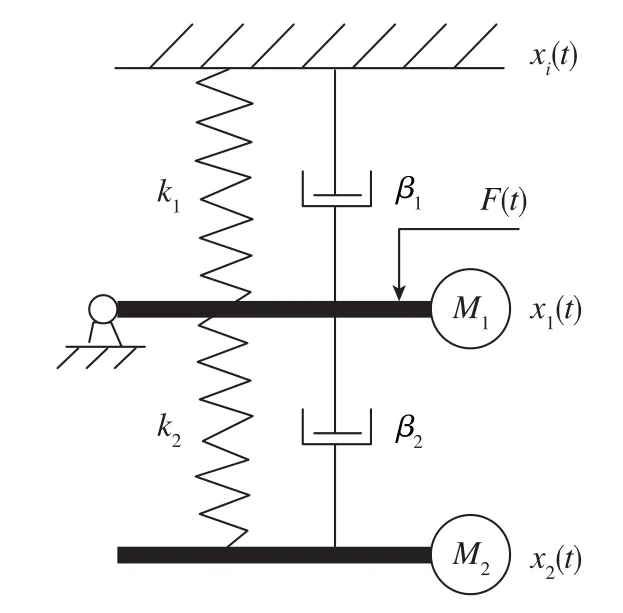
图15 二级主动式弹簧摆杆结构隔振系统Fig.15 Two-stage active vibration isolator based on spring-beam structure

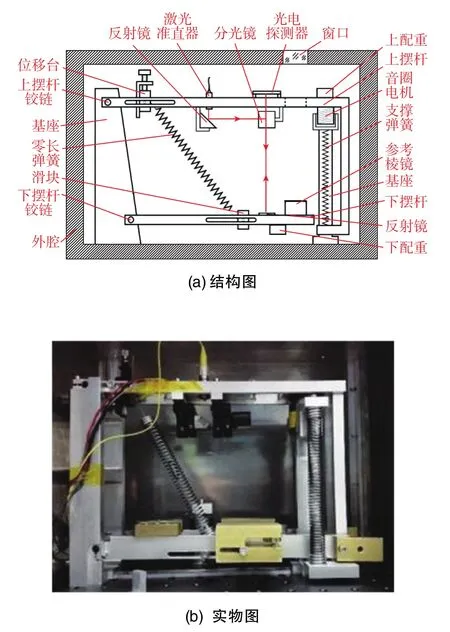
图16 王观等提出的隔振系统Fig.16 Vibration isolation proposed by Wang

2017年，清华大学的要佳敏等提出了一种特殊弹簧振子结构的二级主动式隔振系统，其采用了几何负刚度弹簧结构来替代Superspring中的第二级主弹簧[46]。与传统主动式隔振中使用的螺旋弹簧相比，该结构的垂直尺寸大大减小，且可以通过调节钢片的水平压缩率来适应不同大小的负载。以该结构为第二级弹簧搭建的隔振系统如图17所示[46]，系统的本征周期达到19.2s，与Superspring相比高度降低了近一半。该系统已在T-1型绝对重力仪上进行测试，隔振效果良好。

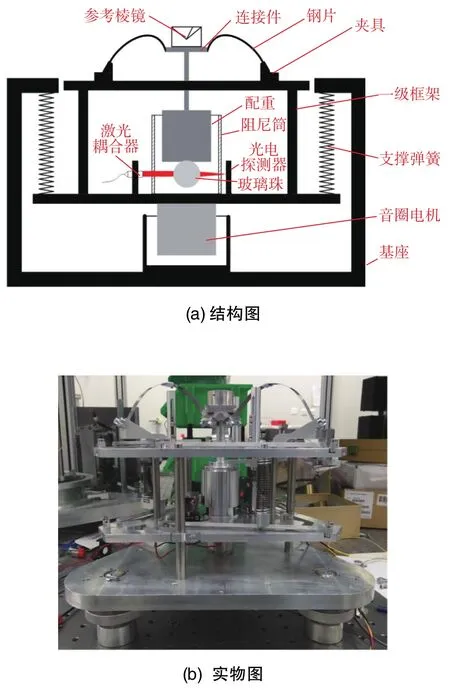
图17 要佳敏等提出的隔振系统Fig.17 Vibration isolation proposed by Yao

3 结论

随着绝对重力测量的发展，已有众多国内外研究机构为自由落体式和原子干涉式绝对重力仪研发了不同种类的超低频垂直隔振系统。普遍来看，和振动补偿方法相比，采用隔振系统来处理地面振动对测量造成的干扰，可以使绝对重力仪具有更高的测量精度。超低频垂直隔振系统从工作原理上可以分为被动式和主动式，其中主动式又包括一级主动式和二级主动式；从机械结构上可以分为弹簧振子式和弹簧摆杆式等。

总体而言，被动式隔振系统可以承受较大负载，结构简单，但对结构的装配和调试精度依赖很大。由于弹性材料存在蠕变和易受环境温度影响的问题，系统的抗干扰能力较差，难以保持长时间的低频率工作。因此，其性能普遍逊色于主动式隔振系统。一级主动式隔振系统的抗干扰能力有所提高，具有较好的性能；二级主动式隔振系统结构复杂、技术难度大，但具有相对而言最好的性能，可以实现较长时间的稳定工作，在绝对重力仪中应用最为广泛，如美国Micro-g LaCoste公司研发的Superspring。

在主动式隔振中，弹簧振子结构的隔振系统与弹簧摆杆结构的隔振系统各有利弊。前者的优点是振子与地面没有刚性连接，缺点是需要额外的约束限制振子除竖直方向以外的自由度；后者的优点是摆杆转轴可以确保摆杆只在竖直平面内运动，缺点是此时摆杆通过转轴与地面刚性连接，地面振动会通过转轴内的铰链传递到被隔振物体上。

目前，我国已在超低频垂直隔振系统领域取得了显著进展，包括中国科学院武汉物理与数学研究所、清华大学等单位在内的多家研究机构已研发了基于不同原理的隔振系统，并在高精度绝对重力仪上验证了其工作性能。在进一步提高便携性、稳定性和可靠性的基础上，这些系统有望应用于我国的多项绝对重力测量任务中。