基于Wardrop第二原理的中转旅客换乘紧张度优化模型研究
2019-08-01葛庆红上海理工大学上海200093
葛庆红,韩 印 (上海理工大学,上海 200093)
GE Qinghong,HAN Yin (University of Shanghai for Science and Technology,Shanghai 200093,China)
0 引言
当前旅游业的发展带动着机场客流量的递增,为适应发展,航空公司需要在机场增设卫星厅,新增的卫星厅有效提升了机场的服务能力,但卫星厅对中转航班旅客的换乘也带来了一些问题,同时对登机口的分配提出了新的挑战。
航班—登机口分配问题是最优化分配包括最小化使用登机口数量、最小化旅客的中转时间两个部分,它们之间相互约束,构成一个整体上的运筹学优化问题[1-3]。现有的研究一般采用按阶段次序分解成子问题的方式求解[4-6],陈欣等[7]研究成果表明合理指派停机位可以降低旅客步行距离,提高机场服务水平。Haghani等[8]在最小化旅客航站楼内的步行距离时,综合考虑了航班之间的转机旅客数量和停机位之间的距离,更加有效降低旅客步行距离。Yan等[9]针对乘客行走路程与等待时间建立了整数规划模型,该模型较好地体现了乘客登机前的整个过程。刘君强等[10]研究了实时登机口分配问题,并提出了相关分配算法。
目前为止,研究航班和登机口分配问题和减少乘客步行距离的专家和学者有很多[11-13],成果颇丰,研究对象通常为同一航站楼,登机口优化分配模型较成熟,但针对中转乘客换乘的登机口分配模型显得不足,且现有的模型进行登机口分配时缺乏对中转乘客换乘时间和中转乘客前后航班连接时间的考虑。本文以新建卫星厅和航站楼为研究对象,考虑中转乘客换乘时间和中转乘客前后航班连接时间两个主要因素,定义了“换乘紧张度”这一概念,以最小化换乘紧张度为目标对登机口优化分配进行建模,并同时考虑最小化登机口使用数量。
1 优化方法的基本思想
本文采用上海浦东国际机场提供的相关资料。卫星厅和航站楼之间设置有捷运路线相连接,国际国内旅客可以在两区域之间快速往来,单程需要8分钟,即h,同一个登机口的两航班之间的间隔时长不少于45分钟,即0.75h,且中转航班对应到达、出发的两个航班须分配在相同登机口。
1.1 问题分析。中转航班与登机口的匹配不仅需要考虑到达/出发类型、宽窄机体的匹配,还需考虑到时间的限制,这是一个复杂的问题,为简化建立模型的难度,本文采用集合分类的思想的基础上循序渐进的进行匹配建模。
中转航班的类型众多,按到达/出发可分为4类,分别用集合pn表示,如表1所示。
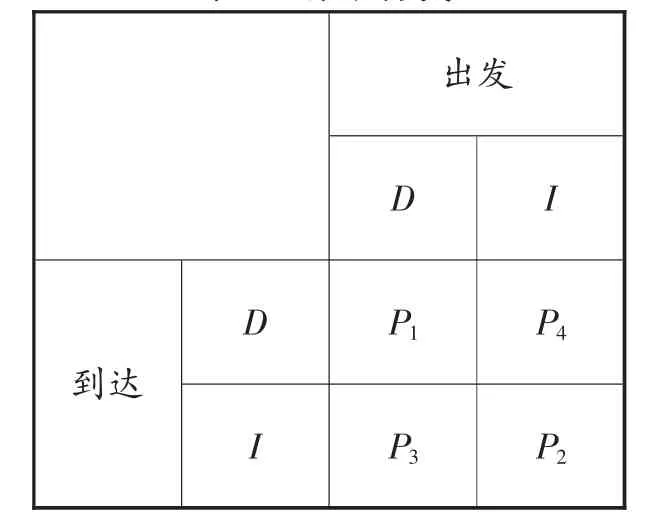
表1 航班分类
登机口(上海浦东国际机场)可分为6类,分别用集合gm表示,如表2所示。

表2 登机口分类
为将简化问题建模,综合表1和表2的信息,按到达/出发的规则将登机口和航班进行初步匹配,匹配结果如表3所示。
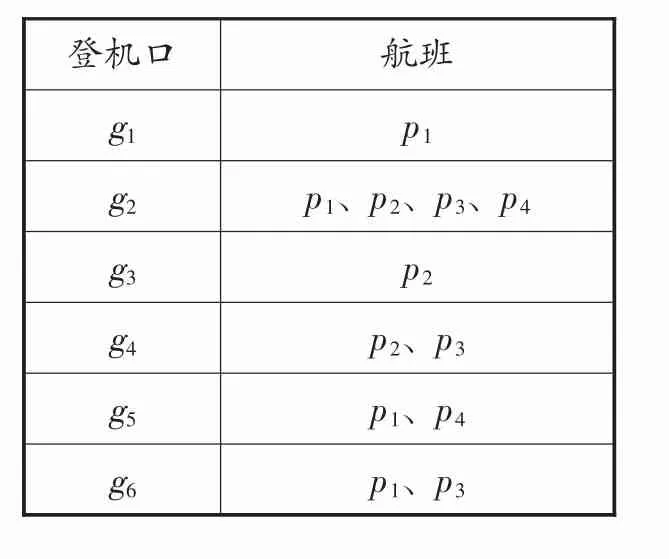
表3 航班—登机口初匹配
1.2 换乘紧张度。首先本文对换乘紧张度的定义如下:

其中:旅客换乘时间=行走时间+最短流程时间+捷运时间;航班连接时间=后一航班出发时间-前一航班到达时间
1.3 Wardrop第二原理的应用。交通规划领域进行交通分配时,通常采用Wardrop第一、第二原理,Wardrop第一原理从用户角度考虑,强调用户平衡;Wardrop第二原理从系统的角度考虑,强调系统最优;其中Wardrop第二原理为:车辆在网络上的分布,使得网络上所有车辆的出行时间最小[14]。
本文基于此原理将乘客的到达、出发航班视为一组OD对,中转乘客的换乘时间即交通阻抗,在登机口布局信息已知的情况下,分配各OD对的登机口进行优化建模,使得所有OD对的换乘紧张度最小即原理中的出行时间最小。
2 模型建立
2.1 目标函数。首先定义两个0-1变量:

k旅客记录号的捷运时间如式(1)所示:

式中,sk表示第k个旅客记录号中的人数;xk表示第k个旅客记录号的到达航班号;yk表示第k个旅客记录号的出发航班号表示集合g中jm登机口到集合中登机口的捷运次数,其数值在表1中可以查到。表示严格约束到达航班和出发航班必须与旅客记录号中的航班信息是一一对应,否则该值为
k旅客记录号的行走时间如式(2)所示。

k旅客记录号的最短流程时间如式(3)所示。表示乘客从集合gm中j登机口到集合


式中,lyk表示k旅客记录号中出发航班的时刻;lxk表示k旅客记录号中到达航班的时刻。k旅客记录号的换乘紧张度如式(5)所示。

第一个目标函数为所有的中转旅客记录号中的旅客换乘紧张度最小,即如式(6)所示。

在减少乘客紧张度的同时,需要同时兼顾机场的运营成本,即尽量减少登机口的使用数。

定义如下0-1变量。第二个目标函数即最小化登机口的使用数量,如式(7)所示。

2.2 约束条件。首先针对机型定义两个0-1变量。

约束中相关参数的取值如下:
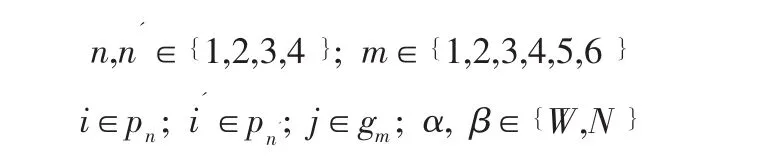
所述的机型约束即到达航班的机型与其分配的登机口机型严格一致,如式(8)所示。

所述的同一登机口的两航班之间的空挡间隔时间必须大于等于0.75h(45min),如式(9)、(10)、(11)所示。

从到达/出发类型角度出发,约束有:g1中的登机口只对P1中的航班服务,如式(12)所示。

g3中的登机口只对P2中的航班服务,如式(13)所示。

g4中的登机口
只对P2、P3中的航班服务,如式(14)所示。

g5中的登机口只对P1、P4中的航班服务,如式(15)所示。

g6中的登机口只对P1、P3中的航班服务,如式(16)所示。

每一个转场飞机号中的航班最多分配一个登机口,如式(17)所示。

3 模型分析
以往模型多强调登机口的优化分配,来减少机场的运营成本,对以中转旅客为对象的登机口分配优化模型研究目前尚未检索到。本文建立的双目标优化模型相对传统的登机口优化分配模型具有以下特点:(1)以往登机口分配模型较少考虑到乘客出行的换乘行为,本模型考虑出行换乘行为,优化目标为双目标,分别为换乘紧张度和登机口使用数量,可以中转旅客换乘紧张度最小为目标进行第一次求解,在求解结果的基础上以登机口使用数量最少为目标进行第二次求解,从而达到最小化中转旅客换乘紧张度的同时优化登机口使用数量。(2)模型在建立的过程中充分考虑到了信息交互,同时优化中转旅客前后航班的登机口分配,来减小中转乘客的换乘紧张度。(3)模型优化方法的思想是Wardrop第二原理,基于Wardrop第二原理对问题进行分析与数学建模,理论支撑更加成熟。(4)本文的优化模型以新建卫星厅机场为研究对象,选用登机口匹配准则等作为约束,在现实中将具有较好的实用价值。
4 结论
本文基于Wardrop第二原理对新增卫星厅机场中的中转旅客换乘紧张度进行了优化研究,将乘客的到达和出发航班视为一组OD对,在航班—登机口的匹配规则基础上考虑信息交互,以换乘紧张度、登机口使用数量为目标和航班—登机口匹配规则为约束建立了双目标优化模型,从而在优化中转乘客换乘紧张度的同时尽量减少了登机口的数量。未来在数据允许的条件下,学者可以针对中转旅客利用该模型对实际生活中的航班卫星厅登机口分配进行实例分析。
