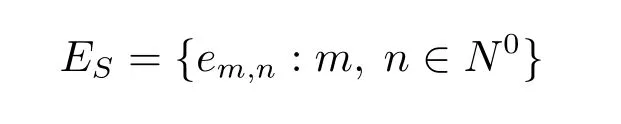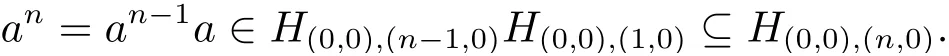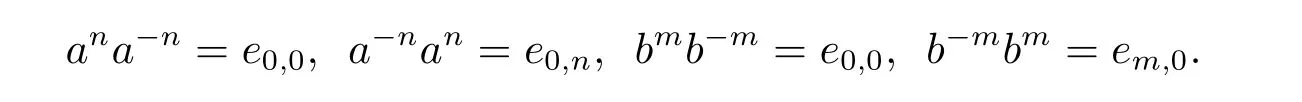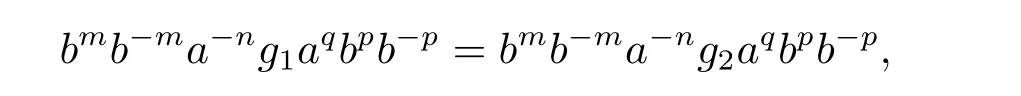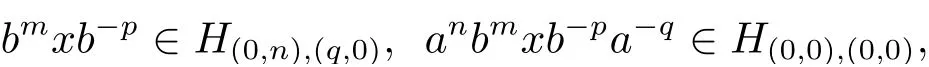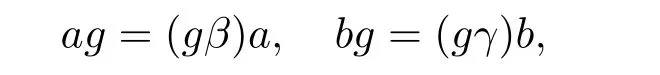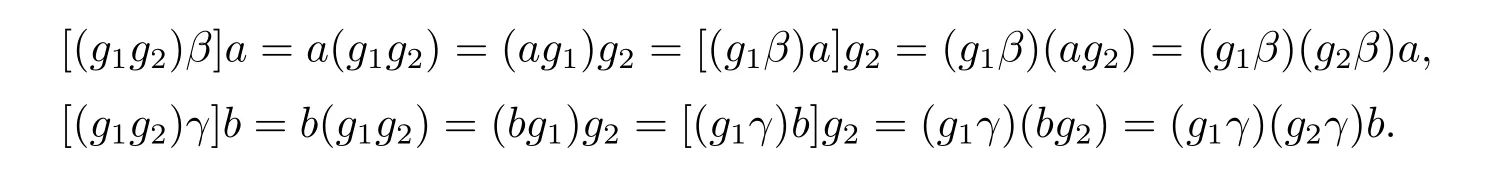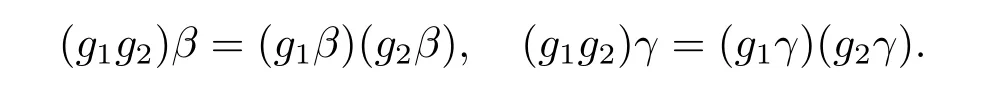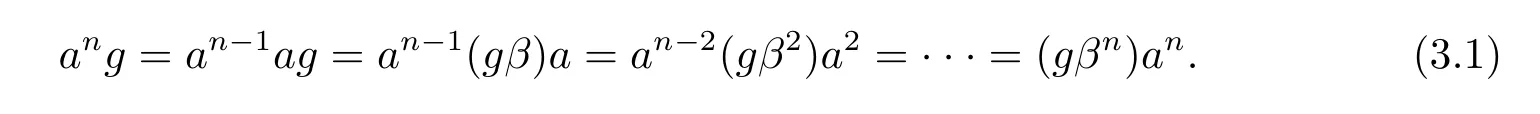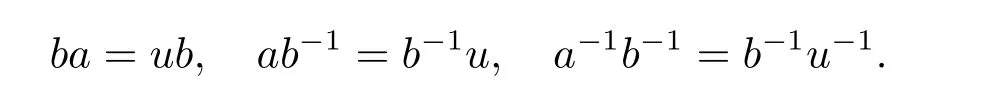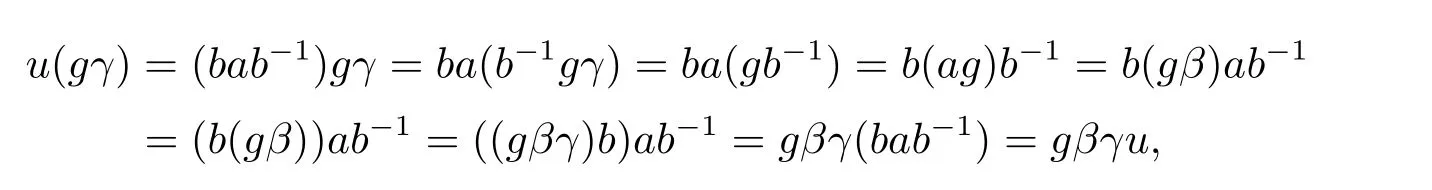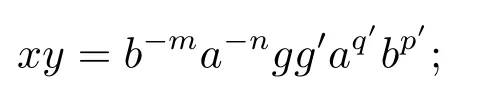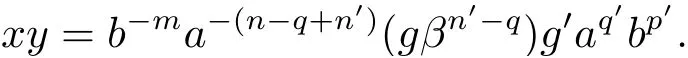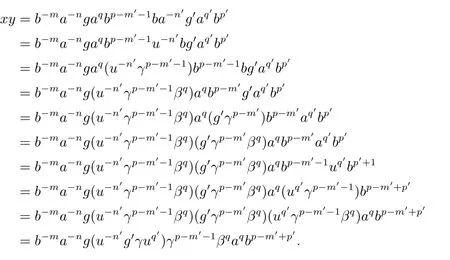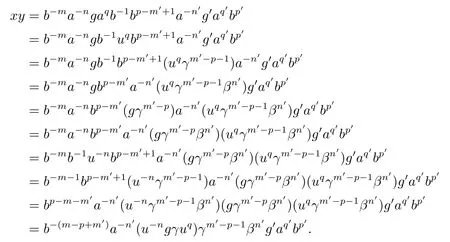正则双单ω2-半群
2019-07-31汪立民冯莹莹
汪立民,商 宇,冯莹莹
(1.华南师范大学数学科学学院,广东广州510631)
(2.普洱学院数学与统计学院,云南普洱665000)
(3.佛山科学技术学院数学系,广东佛山528000)
1 引言及背景知识
在文献[1]中,通过对群G 进行Bruck-Reilly 扩张,Reilly 获得了正则双单ω-半群的BR(G,θ)结构.Warne 研究了正则双单ωn-半群,他在文献[2]中证明了正则双单ωn-半群具有(G×Cn,◦)的结构,其中G 为群,Cn为2n-循环半群,“◦”是一种乘法.本文将用文献[1]的方法研究正则双单ω2-半群.在本节中,引入了ω2-链;在第2 节中,将引入幺半群T 的一种广义Bruck-Reilly 扩张,然后通过群G 的关于它的两个同态β,γ 及它的一个元u 的广义Bruck-Reilly 扩张,得到正则双单ω2-半群;在第3 节中,将证明任意一个正则双单ω2-半群都可以这样构造.
我们将使用文献[3,4]的概念及记号,其余相关概念参见文献[3–16].在本文中,映射作用在元素上都统一用映射写在元素的右侧来表示.设a,b 为半群S 的元,若S1a=S1b,则称a,b 是L-相关的.若aS1=bS1,则称a,b 是R-相关的.规定H=L ∩R 且D=L ∨R.可知L,R,H 和D 是S 上的等价关系且满足H ⊆L ⊆D,H ⊆R ⊆D 及D=L ◦R=R ◦L.为了避免混淆,记S 上的关系K 为K(S).用La记S 上包含a 的L-类,Ra记S 上包含a的R-类.若半群S 只含一个D-类,则称它是双单的.若对半群S 的任一元a,存在唯一的S 的元x,满足axa=a 且xax=x,则称半群S 为逆半群,称x 为a 的逆元,记为a−1.用ES表示半群S 的幂等元的集合.在ES上定义偏序“≤”为e ≤f 当且仅当ef=fe=e.设S 为半群且Cω={e0,e1,e2,···},其中e0,e1,e2,···为幂等元且e0>e1>e2>···,若则称S 为ω-半群.用N 0 表示所有非负整数的集合,N 表示所有正整数的集合,T 为具有单位元e 的幺半群,θ 为从T 到T 的单位的群He的同态.在上规定乘法为
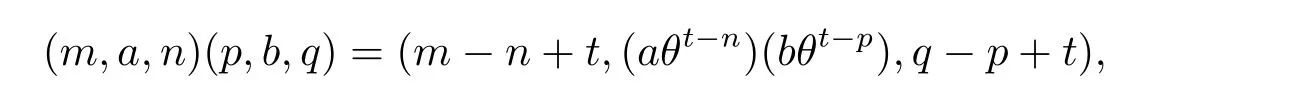
其中t=max{n,p},θ0为T 的恒等映射,则在上述乘法下构成一个半群,称为T 的由θ 决定的Bruck-Reilly 扩张,记为BR(T,θ),可知
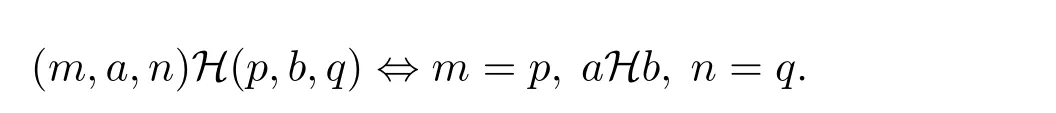
引理1.1[3]设G 为群,θ 为G 的自同态,S=BR(G,θ)为G 的由θ 决定的Bruck-Reilly扩张,则S 为双单逆ω-半群.反之,任一个双单逆ω-半群同构于某一个BR(G,θ).
定义1.2在集合上规定一个序为:(m,n)≤(p,q)当且仅当m>p,或m=p且n ≥q,则称具有这样序的集合为一个ω2-链,记为Cω2.任一个序同构于Cω2的偏序集也称为ω2-链.
若半群S 的幂等元集ES序同构于Cω2,则称S 为ω2-半群.因此,若S 为ω2-半群,则ES={em,n:m,n ∈N0},其中em,n≤ep,q当且仅当(m,n)≤(p,q).用Rm,n表示S 的包含幂等元em,n的R-类,用Lm,n表示S 的包含幂等元em,n的L-类,用H(m,n),(q,p)表示Rm,n∩Lp,q,即

引理1.3[5]设S 为ω2-逆半群,则其中
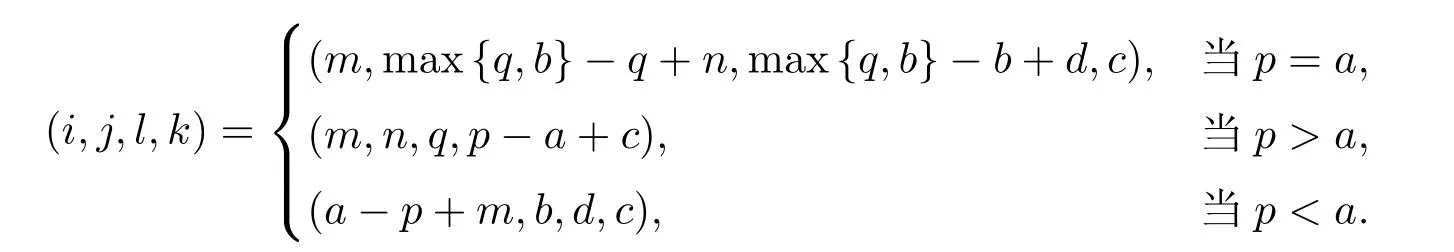
引理1.4设S 为正则ω2-半群,则S 为具有单位元的ω2-逆半群.特别地,双单ω2-半群是双单ω2-逆半群.
证 设S 为正则ω2-半群,e 和f 为S 的幂等元,则e ≤f 或f ≤e,从而ef=fe=e或ef=fe=f.不论何种情况,都有ef=fe.因此S 的幂等元可交换,从而S 为逆半群.设ES={em,n:m,n ∈N0},其中em,n≤ep,q当且仅当(m,n)≤(p,q).设a 为S 的任一元,则存在S 的幂等元em,n,使得aa−1=em,n,因此e0,0a=e0,0(em,na)=(e0,0em,n)a=em,na=a.类似有ae0,0=a,于是e0,0是单位元,故S 为具有单位元的ω2-逆半群.
2 广义Bruck-Reilly 扩张
在这一节中,将引入一种广义Bruck-Reilly 扩张,对群和它的一对同态做这种扩张,可得到正则双单ω2-半群.在下一节中,将证明任一个正则双单ω2-半群都可以这样构造出来.
设T 为具有单位元e 的幺半群,He为T 的包含e 作为单位元的极大子群,u 为He的一个元,τu为He的内部自同构,即对任意g ∈He,有gτu=ugu−1. 设β,γ 为从T到He的两个同态,且满足γτu=βγ,其中β0,γ0为T 的恒等映射,u0=e. 对任意(m,n,t,q,p),(m',n',t',q',p')∈N0×N0×T×N0×N0,在N0×N0×T×N0×N0上规定乘法如下
可以验证(2.1)式满足结合律,由于证明过程是直接的和繁琐的,因此省略了验证过程.规定从BR(T,γ)到N0×N0×T×N0×N 0 的映射φ 为(m,a,n)φ=(m,0,a,0,n).显然φ 为单射.对任意(m,0,a,0,n),(m',0,a',0,n')∈N0×N0×T×N0×N0,有
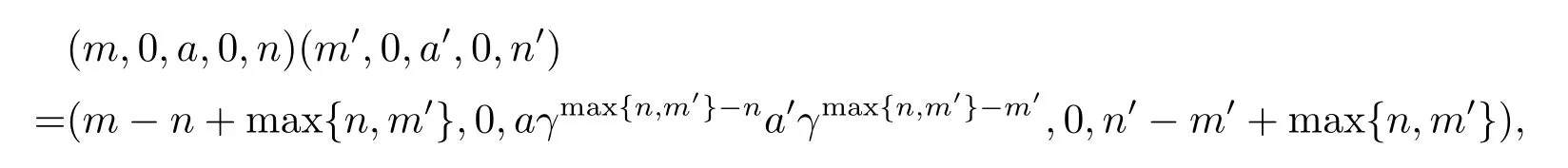
从而φ 为同态. 在这个观点下,称上述构造的半群为T 的由β,γ,u 所决定的广义Bruck-Reilly 扩张,记为GBR(T;β,γ;u).可验证(m,n,a,q,p)为GBR(T;β,γ;u)的幂等元当且仅当m=p,n=q 且a 为T 的幂等元.
引理2.1设S=GBR(T;β,γ;u)为幺半群T 的由β,γ,u 所决定的广义Bruck-Reilly扩张,(m,n,a,q,p),(m',n',a',q',p')为S 的任意元,则
(1)(m,n,a,q,p)R(S)(m',n',a',q',p')当且仅当m=m',n=n'及aR(T)a'.
(2)(m,n,a,q,p)L(S)(m',n',a',q',p')当且仅当q=q',p=p'及aL(T)a'.
证(1)设(m,n,a,q,p),(m',n',a',q',p')为S 的两个元且(m,n,a,q,p)R(S)(m',n',a',q',p'),则存在S 中的元(x,y,b,z,w)使得(m,n,a,q,p)(x,y,b,z,w)=(m',n',a',q',p'),从而
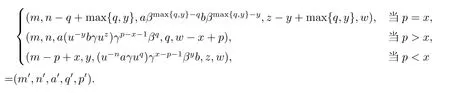
比较第一分量,得m'≥m.对偶地,有m ≥m',从而m=m',因此p ≥x.比较第二分量,得n ≤n'.对偶地,有n ≥n',于是n=n'.若p=x,比较第二分量,得max{q,y}=q,从而

比较第三分量得a'=abβq−y,从而在T 中有Ra'≤Ra.若p>x,比较第三分量,从而在T中有Ra'≤Ra.对偶地,有Ra≤Ra'.故aR(T)a'.
反之,若aR(T)a',则存在T 的元c,d,使得ac=a'且a'd=d,从而
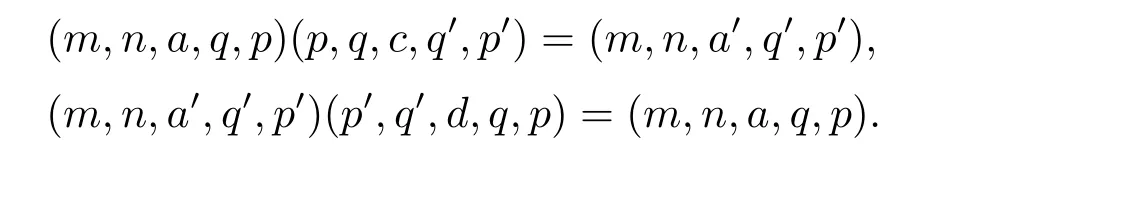
故(m,n,a,q,p)R(S)(m,n,a',q',p').(2)类似可证.
引理2.2设S=GBR(T;β,γ;u)为幺半群T 的由β,γ,u 所决定的广义Bruck-Reilly扩张,则S 为逆半群当且仅当T 是逆半群.
证若T 为逆半群,则对S 的任一元(m,n,a,q,p),有
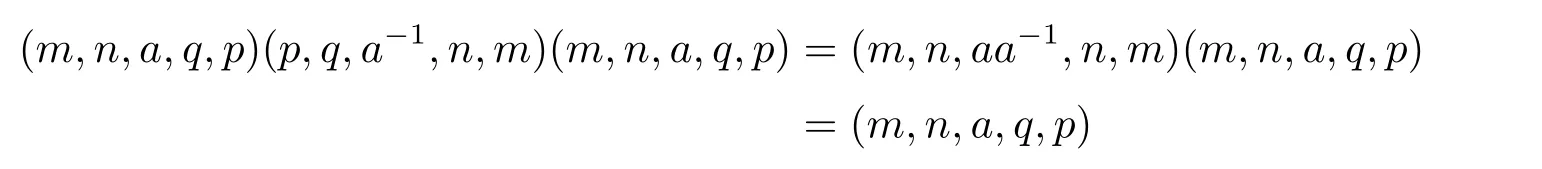
且
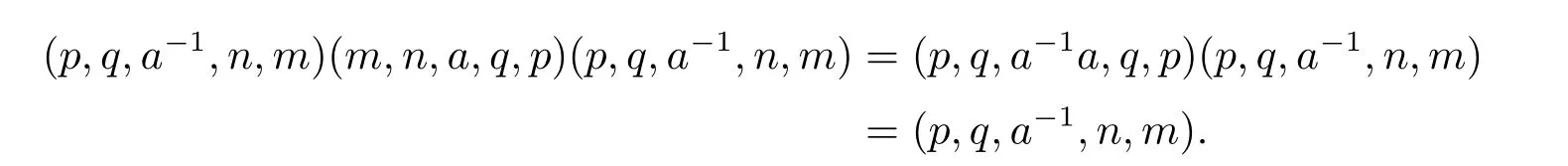
因此(m,n,a,q,p)有逆元(p,q,a−1,n,m),于是S 是正则的.若(m,n,e,n,m)和(m',n',e',n',m')为S 的两个幂等元,则
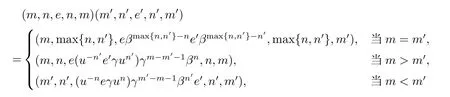
且
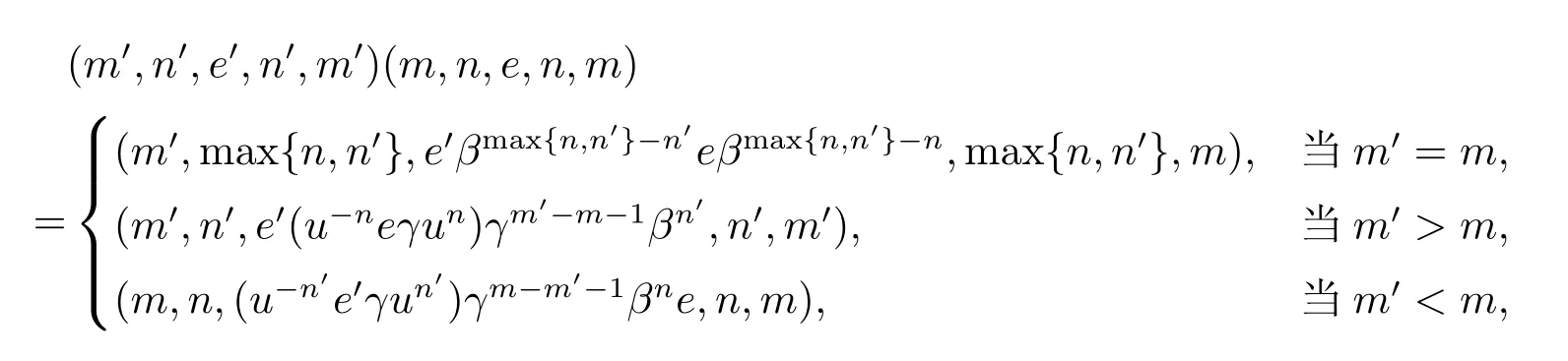
由于T 为逆半群,幂等元可交换,从而S 的幂等元是可交换的.
反之,若S 为逆半群,设(m,n,a,q,p)−1=(x,y,b,z,w),则

是幂等元且R-相关于(m,n,a,q,p)且L-相关于(x,y,b,z,w),从而p=x.由于

是幂等元,从而m=w 且n=n −q+max{q,y}=z −y+max{q,y}=z,因此q=y,于是
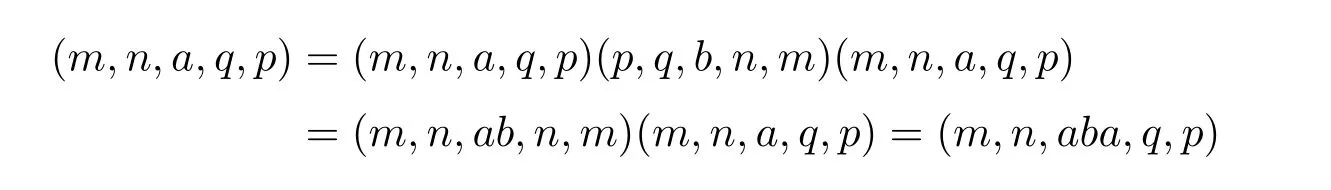
且
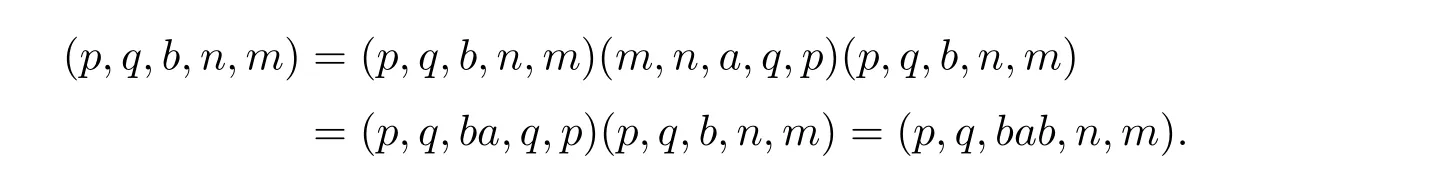
故在T 中有a=aba 且b=bab,从而T 是正则的.若e,f 为T 的两个幂等元,由于
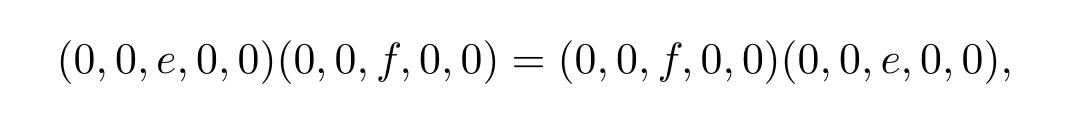
从而ef=fe.因此T 为逆半群.
定理2.3设G 为群且单位元为e,u 为G 的元,β 和γ 为G 的同态,S=GBR(G;β;γ;u)为G 的由β,γ,u 决定的广义Bruck-Reilly 扩张,则S=GBR(G;β,γ;u)为正则双单ω2-半群.
证由引理2.2 知,S 为正则半群.设(m,n,a,q,p),(m',n',a',q',p')为S 的任意两个元,则
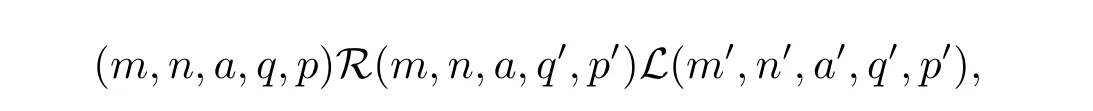
从而(m,n,a,q,p)D(m',n',a',q',p'),因此S 是双单的.设(m,n,e,n,m),(m,n',e,n',m)为S 的任意两个幂等元且n 若(m,n,e,n,m),(m',n',e,n',m')为S 的两个幂等元且m 从而(m',n',e,n',m')<(m,n,e,n,m),因此S 的幂等元构成一个链 对任意m,n ∈N0,规定em,n=(m,n,e,n,m),从而S 的幂等元的集合为{em,n:m,n ∈N0}且em,n≤ep,q当且仅当(m,n)≤(p,q).因此S=GBR(G;β,γ;u)为正则双单ω2-半群. 在本节中,我们将证明任一个正则双单ω2-半群同构于群G 的由β,γ,u 决定的Bruck-Reilly 扩张GBR(G;β,γ;u). 设S 为正则双单ω2-半群,ES为S 的幂等元的集合,则 构成ω2-链且em,n 从而对任意非负整数n,有an∈H(0,0),(n,0).类似地,设m,n 为非负整数,则 且 由引理1.3,对H(0,0),(0,0)的任意元g,有b−ma−ngaqbp∈H(m,n),(q,p).对任意m,n,p,q ∈N0,规定从H(0,0),(0,0)到H(m,n),(q,p)的对应法则σ 为gσ=b−ma−ngaqbp.若b−ma−ng1aqbp=b−ma−ng2aqbp,则 从而a−ng1aq=a−ng2aq,因此 于是g1=g2.设x 为H(m,n),(q,p)的任意元,则 从而(anbmxb−pa−q)σ=x,因此σ 为双射. 引理3.1设a ∈ H(0,0),(1,0)且b ∈ H(0,0),(0,1),则S 的任一元都可唯一的表为b−ma−ngaqbp的形式,其中m,n,p,q ∈N0,g ∈H(0,0),(0,0). 设H(0,0),(0,0)=G,g 为G 的任一元,则ag ∈H(0,0),(1,0)H(0,0),(0,0)⊆H(0,0),(1,0)且bg ∈H(0,0),(0,1)H(0,0),(0,0)⊆H(0,0),(0,1),从而由引理3.1 知ag 可唯一的表示为b0a0g'a1b0=g'a;bg可唯一的表示为b0a0g''a0b1=g''b,其中g',g''∈G.设β,γ 分别为G 的按如下条件所决定的映射 则 由于aa−1=e0,0且bb−1=e0,0,从而 因此β,γ 为G 的自同态.于是对任意n ∈N0,有 进一步地,由于ga−n∈H(0,n),(0,0)且ana−n=e0,0为S 的单位元,从而 类似地,对任意n ∈N0,有 令u=bab−1,则u−1=ba−1b−1.规定u0=e0,0.由于 从而ba−1=u−1b.类似有 因此,对任意m,n,q,p ∈N0,有 引理3.2设S 为正则双单ω2-半群,G 为S 的单位的群,a ∈H(0,0),(1,0),b ∈H(0,0),(0,1),则u=bab−1∈G 且γτu=βγ,其中τu为G 的内部自同构,即对任意g ∈G,gτu=ugu−1. 证由知且对任意g ∈G,有 因此对任意g ∈G,有gγτu=ugγu−1=gβγ,于是γτu=βγ. 定理3.3设S 为正则双单ω2-半群,则SGBR(G;β,γ;u),其中G 为群,β,γ 都为G 的自同态,u ∈G. 证设G,β,γ,u 如前述所规定.由引理3.1 知,S 的每一元都可唯一表示为b−ma−ngaqbp的形式,其中m,n,p,q ∈N0,g ∈G.设x=b−ma−ngaqbp,y=b−m'a−n'g'aq'bp',其中g,g'∈G.分以下三种情形. 情形1若p=m',则 若q=n',则 若q>n',则由(3.1)式知 若q 情形2若p>m',则由(3.1),(3.3),(3.4)式知 情形3若p 因此从S 到GBR(G;β,γ;u)的映射

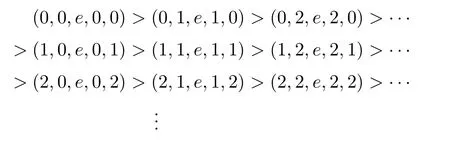
3 结构定理