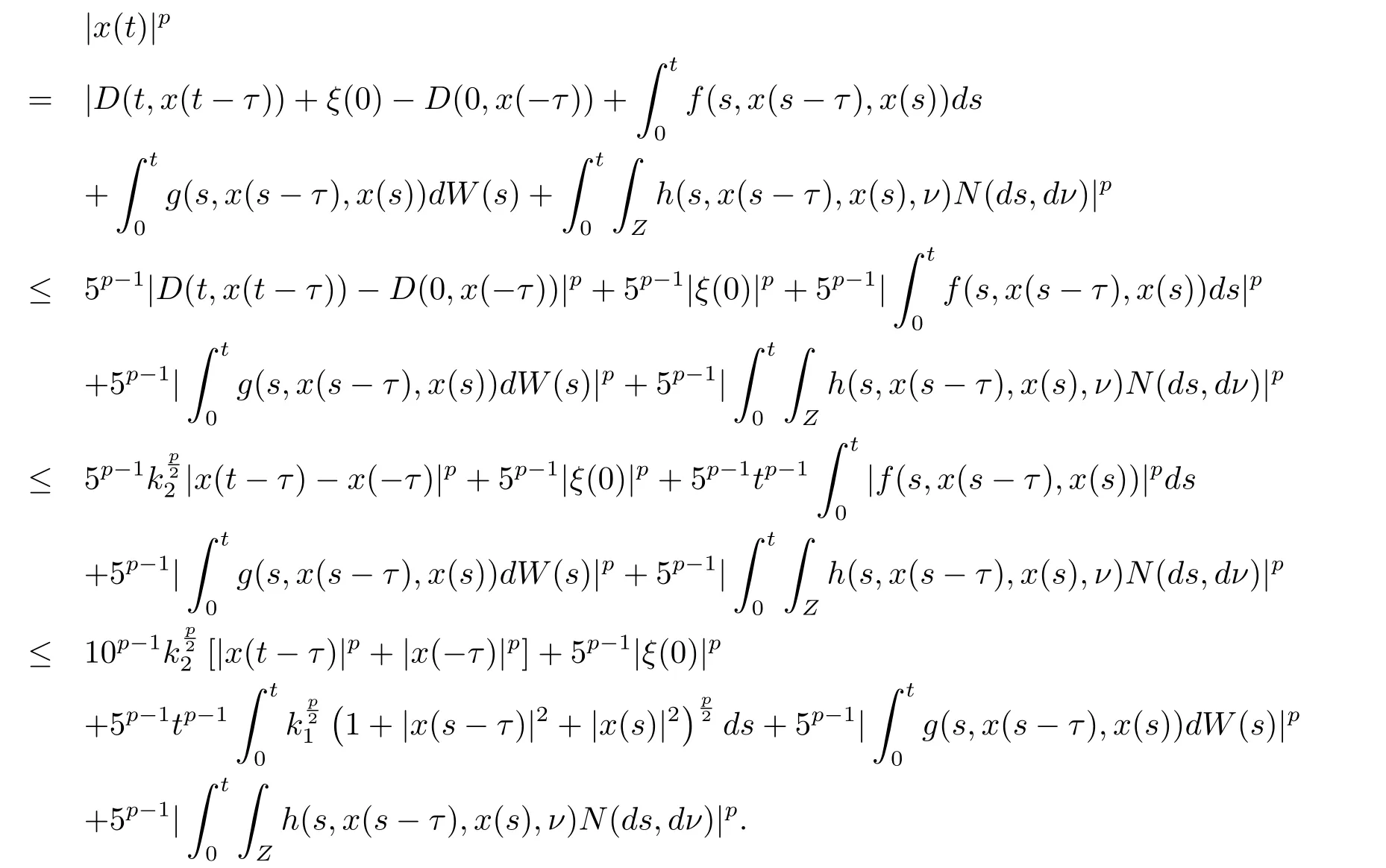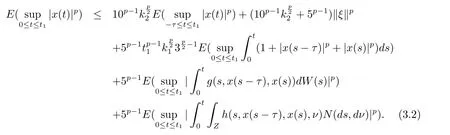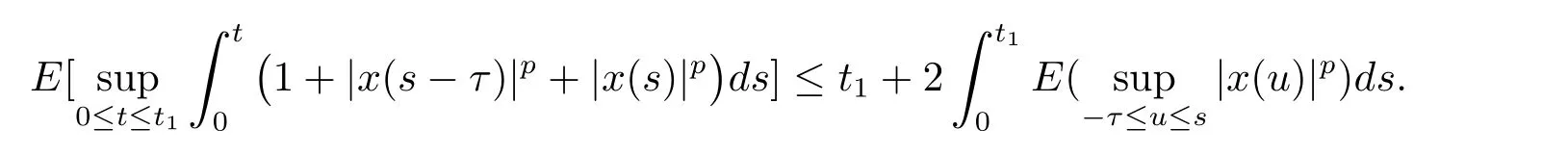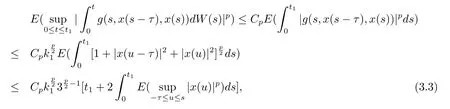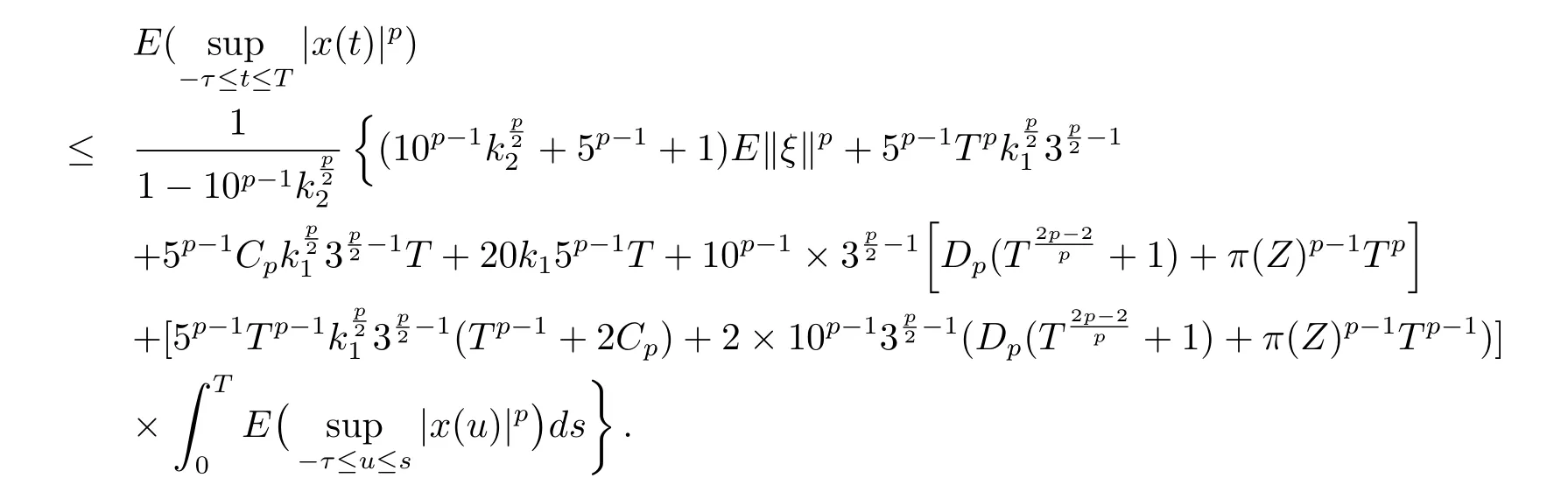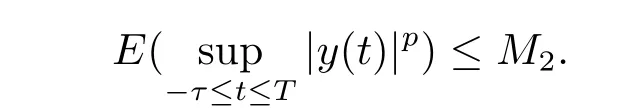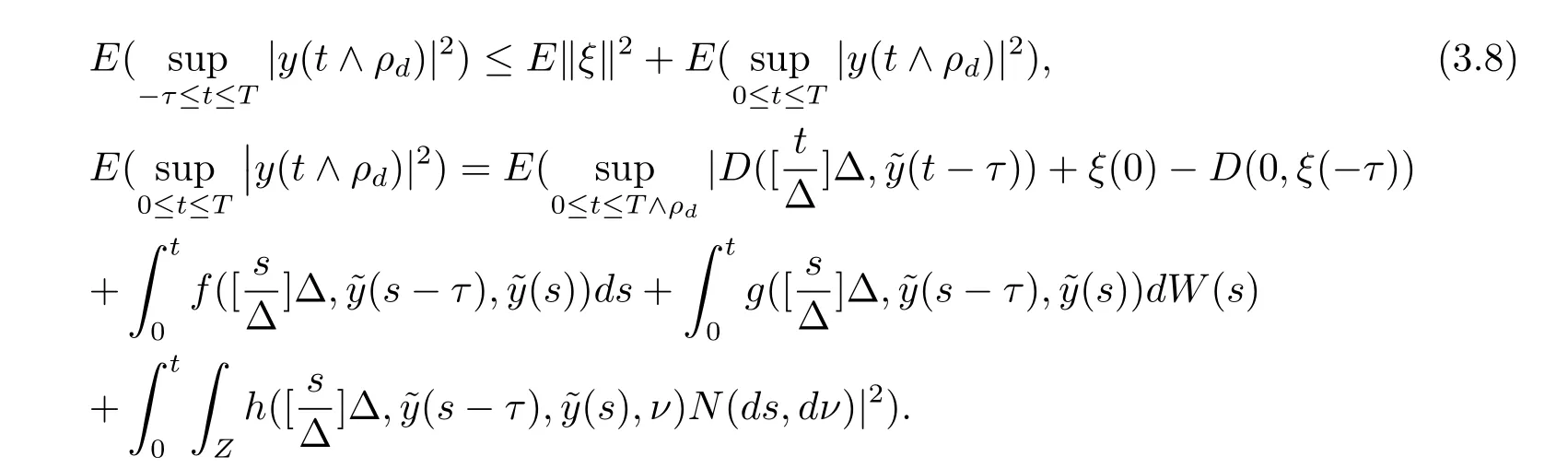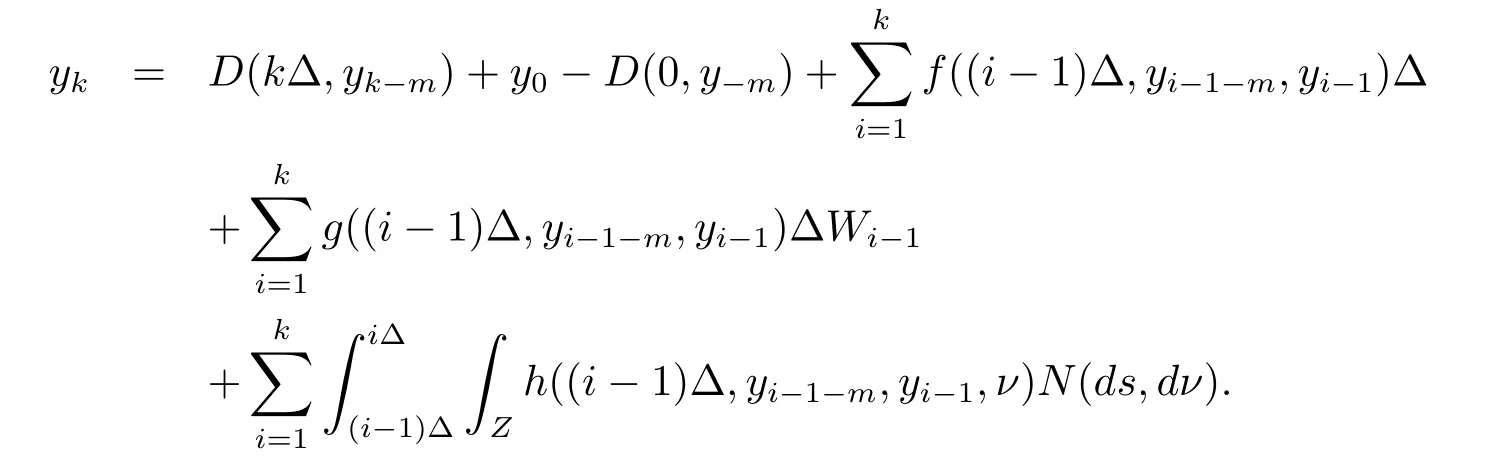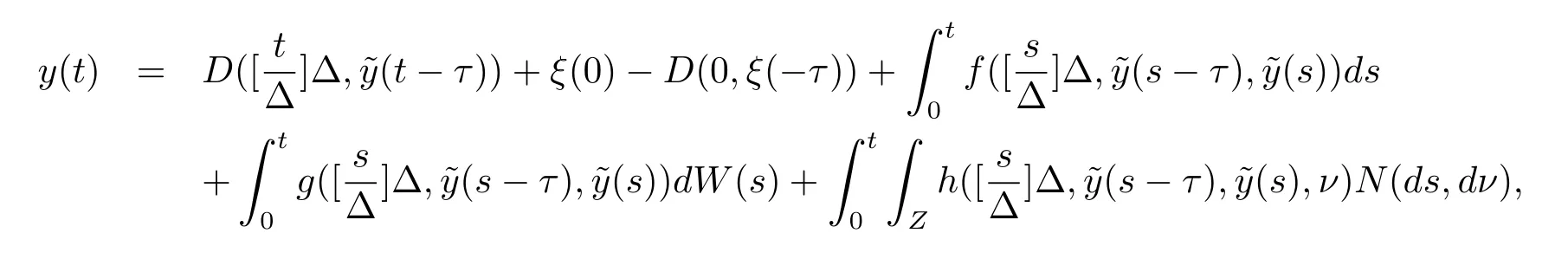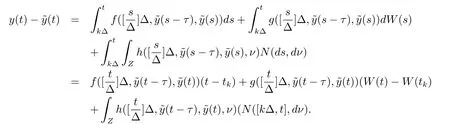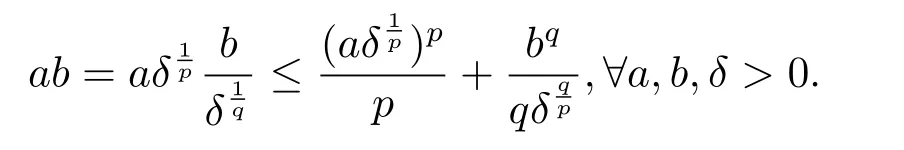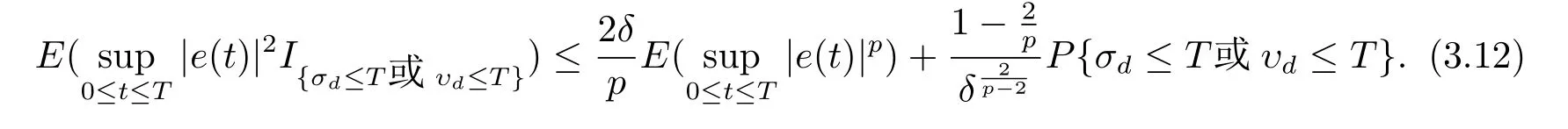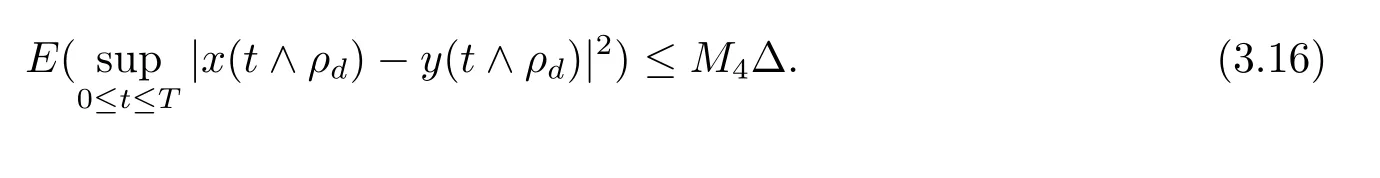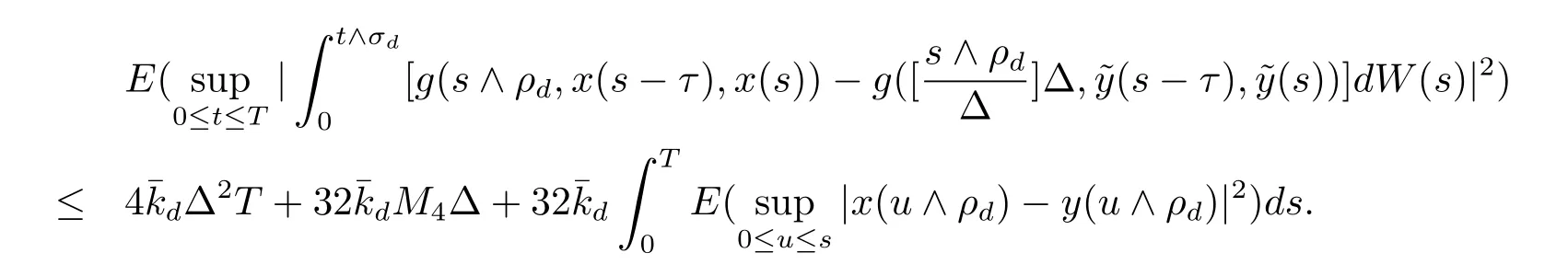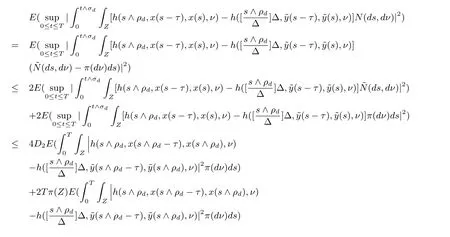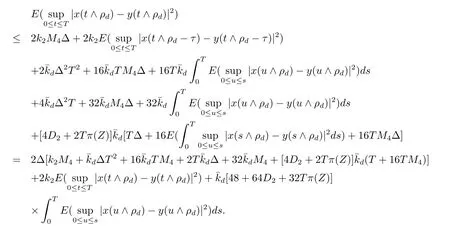带Lévy 跳的中立随机微分方程的EM 逼近
2019-07-31严良清韩新方
马 丽,严良清,韩新方
(海南师范大学数学与统计学院,海南海口571158)
1 引言
中立延迟随机微分方程历年来在生物、工程、金融等各个领域引起了学者的广泛关注.文[1]系统地介绍了不带跳的随机泛函微分方程的基本理论及其在金融、随机游戏、人口问题中的应用;文[2]给出了带有Lévy 跳随机泛函微分方程解的存在唯一性;文[3]得到了一类带Lévy 跳的中立随机泛函微分方程解的存在唯一性;文[4]研究了带有特殊跳(泊松跳)的中立随机延迟微分方程的数值逼近;文[5]得到了Lévy 噪声扰动的混合随机微分方程的Euler 近似解;文[6]和文[7]研究了带Markov 状态转换的跳扩散方程的数值解.
设(Ω,F,P)是完备概率空间,(Ft)t≥0是其上一个满足通常条件的适应流. 设{=(t),t ≥0}是一个关于(Ft)t≥0适应的稳定的Rn值泊松点过程. 设B(Rn−{0})为Rn−{0}上的波莱尔σ-代数,对A ∈B(Rn−{0}),定义与联系的泊松计数测度N(t,A)=N((0,t]×A)如下

则存在一个σ 有限测度π 使得
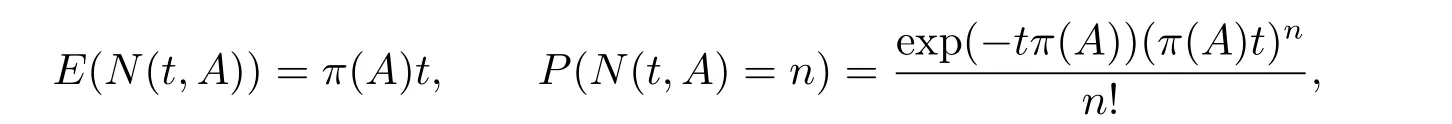
这里的测度π 称为Lévy 测度.由Doob-Meyer 分解定理,存在关于(Ft)t≥0适应的唯一的鞅和唯一的增过程使得

设|·|表示欧式空间Rd中的范数,τ 为一个正的固定的延迟,C([−τ,0],Rd)为[−τ,0]到Rd上的连续函数类,其上的范数为设ξ(t)为关于F0可测的C([−τ,0],Rd)随机变量且满足Eξp<∞,其中p 为大于等于2 的任意正整数. 设W(t)是(Ω,F,P)上关于流(Ft)t≥0适应的标准的r 维布朗运动且与跳N 独立. 设Z ∈B(Rn−{0})且π(Z)<∞,设0 在系数满足局部Lipschitz 条件和线性增长条件,中立项D(t,x(t −τ))关于第二个分量为压缩映射的条件下,类似于文[2],我们可得方程(1.1)存在唯一解.由于解没有显示表达,因此有必要研究其数值解.如果数值解逼近于真实解,我们可以用数值解来估计真实解. 本文内容安排如下:第二节介绍了方程(1.1)的Euler 的数值算法,并给出主要结果即定理1;第三节给出定理1 的证明.本文推广了文[4]的结果,考虑的中立项是时间和状态的二元函数,在逼近的时候对中立项需要加一定的条件才可以放缩.此外,有中立项时需要把它看成一个整体,进而用伊藤公式,再由基本不等式及压缩映射最终得到数值解稳定于真实解.方程(1.1)中f,g,h 也依赖于时间,因此需要三个函数关于时间t 是局部Lipschitz 的. 下面给出(1.1)式的EM 逼近解. 其中∆Wk=Wtk+1−Wtk.假设则EM 逼近解y(t)的连续形式如下 本文对系数做如下假设. (H1) 对任意的正整数m,存在正整数使得对任意的t1,t2∈[0,+∞),任意的且|x|≤m,|y|≤m,|有 (H2)对任意的p ≥2,存在正数k1使得对任意t ∈[0,+∞),x,y ∈Rn,有 (H3)存在正数k2∈(0,1),使得对任意t1,t2∈[0,+∞),x,y ∈Rn,有 设T ∈[0,+∞)为任一常数,本文主要结果如下. 定理1在(H1)–(H3)条件下,方程(1.1)的Euler 数值解收敛到真实解.即 在证明定理1 之前,需要一些重要的引理. 引理1在(H1)–(H3)条件下,对任意p ≥2,存在一个独立于∆的常数M>0,使得 证不失一般性,假定x(t)是有界的,否则的话,对每个整数n,定义停时τn=inf{t ∈[0,T]:|x(t)|≥n},考虑停止过程x(t ∨τn)即可.由基本不等式、假设(H3)及不等式可得 因此对任意的t1∈[0,T],有 显然有 由BDG 不等式及假设(H2)可得 其中Cp为与p 有关的正的常数.对于跳部分,由假设(H2)及文[3]引理3.2,得 其中Dp为正的常数.注意到对任意的t1∈[0,T],有 将(3.2)–(3.4)式代入(3.5)式得 因此 从而定理得证. 下面先建立两个停时, 引理2在假设(H1)–(H3)下,有 这里C1是独立于∆的正的常数. 证对任意的t1∈[0,T], 证明方法与引理1 的方法相同,这里其证明省略. 推论3在假设(H1)–(H3)下有 这里的M2是一个正的常数且独立于∆. 证对任意的t ∈[0,T ∧ρd],存在k 使得t ∈[tk,tk+1),注意到 因此 又 因此 由基本不等式及假设(H2)可得 由推论3,文[2]引理3.2 及文[9]中Lyapunov 不等式得 取M3=3k1T[1+r+2π(Z)](1+2M2)即可,其中r 为布朗运动的维数. 定理1 的证明假设e(t)=x(t)−y(t),易知 因此对任意的δ>0,有 根据引理1,有 由基本不等式得 将(3.13),(3.14)式代入(3.12)式得 根据x(t)和y(t)的定义,有 类似于引理4 中的证明可知 不妨令M4=3k1[1+2M2](∆+m+2π(Z)),则 由假设(H3)及(3.16)式知 由假设(H1)及Hölder 不等式可得 由假设(H1)及BDG 不等式可得 由假设(H1)及文[2]引理3.2 可得 因此 设 将(3.15)、(3.18)式代入(3.11)式得
2 EM 近似解及主要结果
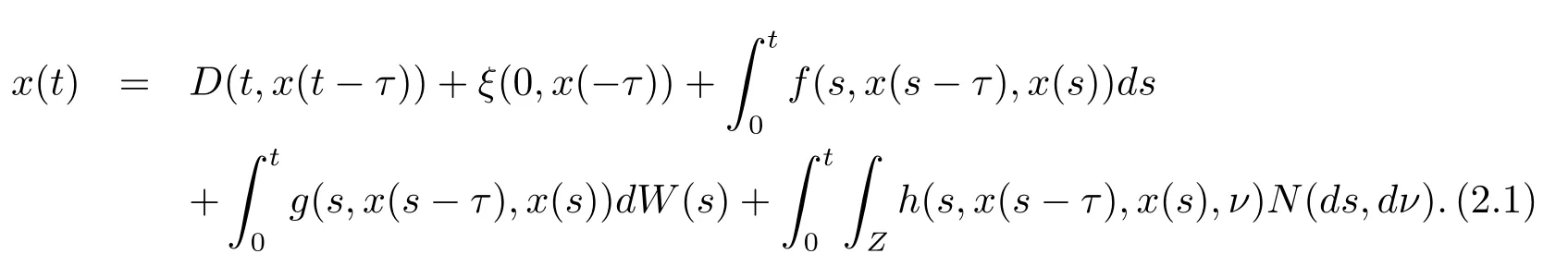
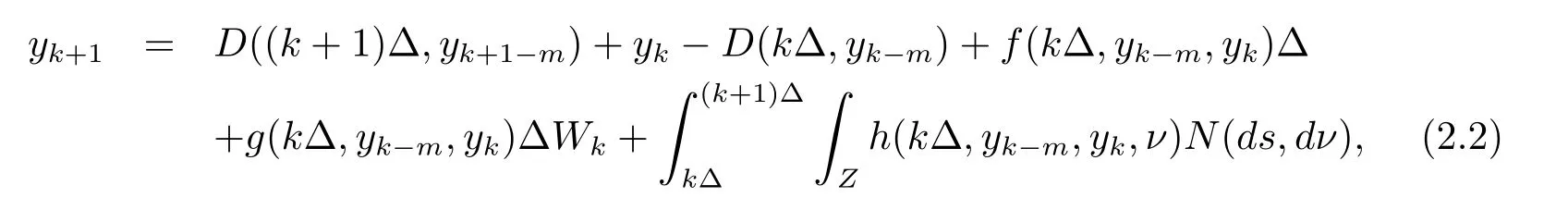

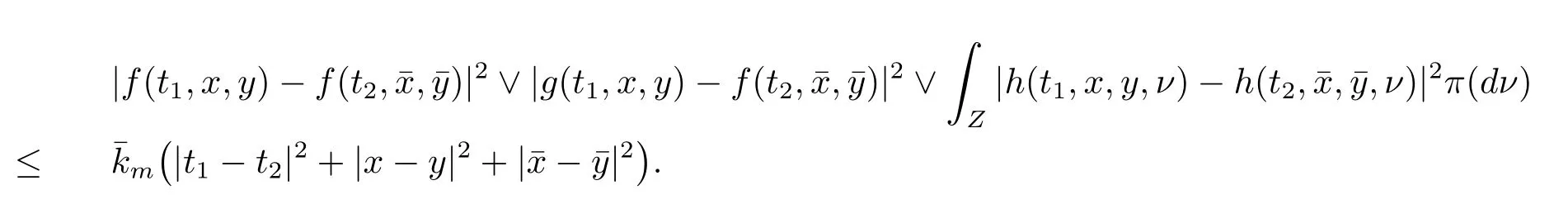

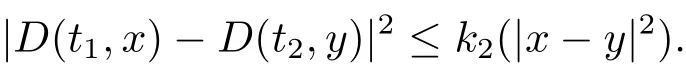

3 定理1 的证明