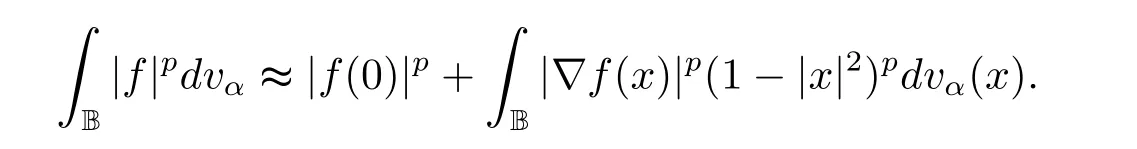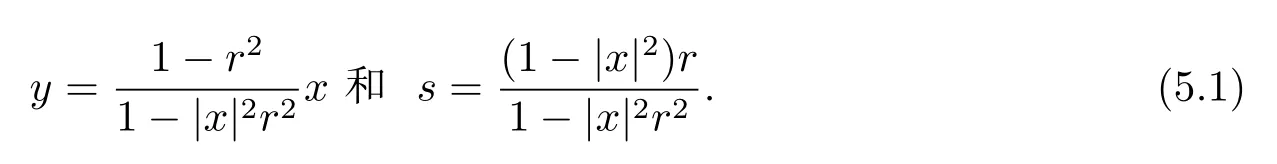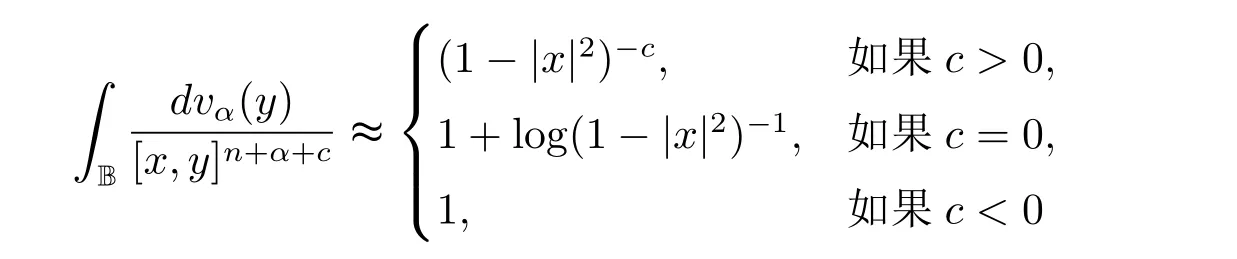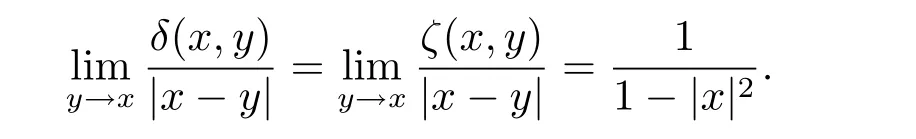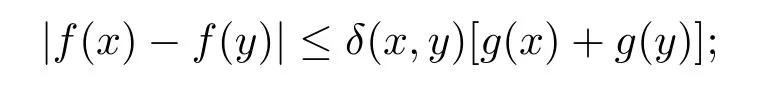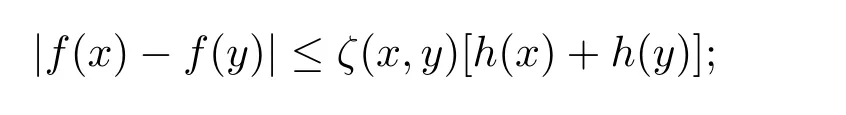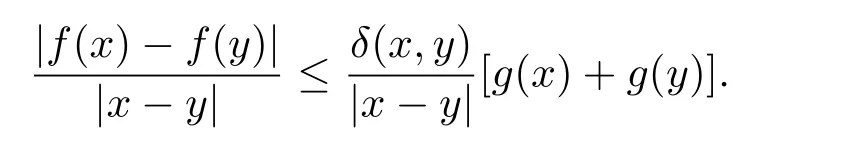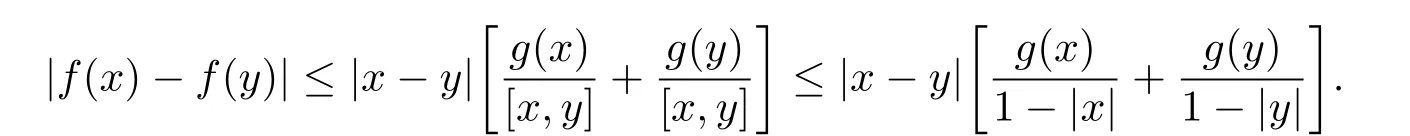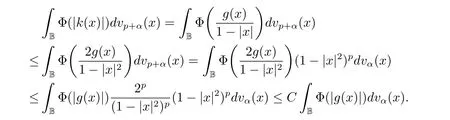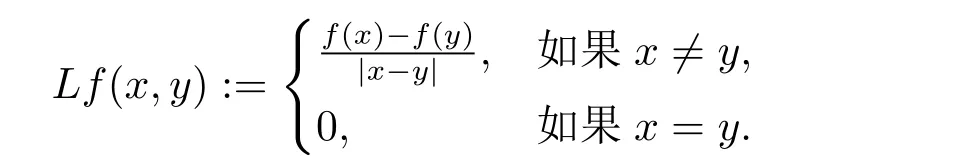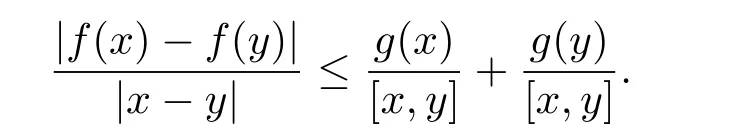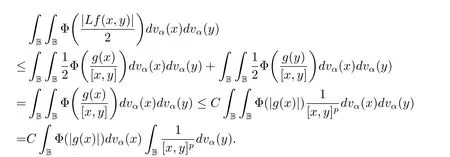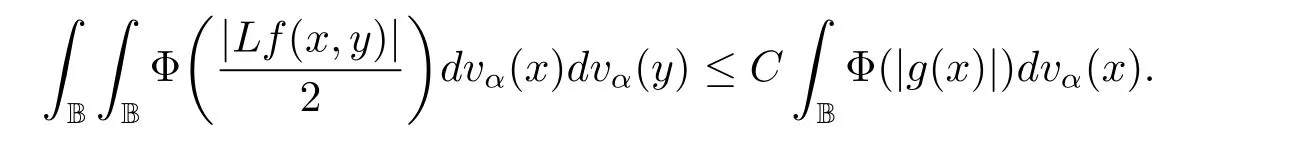调和Bergman-Orlicz 空间的Lipschitz 型刻画
2019-07-31马茹梦徐景实
马茹梦,徐景实
(海南师范大学数学与统计学院,海南海口571158)
1 引言
对于区域Ω ⊆Rn,用h(Ω)表示Ω 上的复值调和函数构成的空间.对于一个固定的正整数n ≥2,用H=Rn−1×R+表示上半空间,其中R+表示所有正实数构成的集合.设α 为实数,用表示H 上的加权测度.给定一个凸函数Φ:[0,∞)→[0,+∞),称Φ是一个增长函数如果它是连续的且非减的函数.对于增长函数Φ,Orlicz 空间
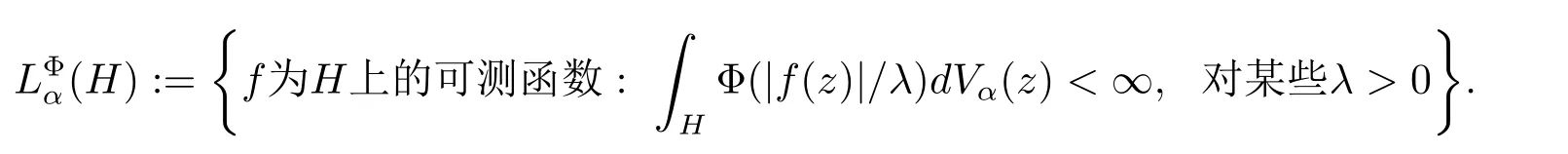
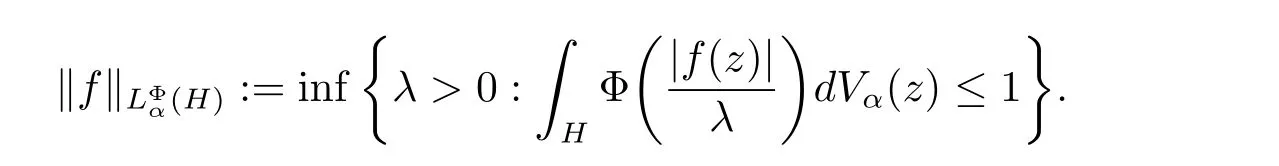
当Φ(t)=tp,t ∈[0,∞)时,Orlicz 空间是Lebesgue空间且对应的调和Bergman-Orlicz空间表示为
乌兰哈斯和朱克和在文献[1]中利用欧氏度量、双曲型度量、伪双曲型度量给出加权Bergman 空间在复欧氏空间Cn的单位球上的Lipschitz 型刻画;Kyesook 在文献[2]中研究了在上半空间H 上的调和Bergman 空间的刻画.即设α>−1,p ∈(0,∞)和则存在一个正的连续函数使得对所有的z,w ∈H 有
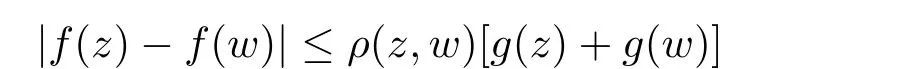
和
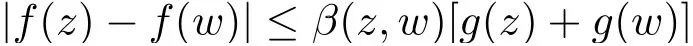

其中ρ 和β 的定义见第二节.文献[2]还给出了上半空间上调和函数差商的刻画和欧氏空间中单位球上调和Bergman 空间的刻画.
受文献[1,2]的影响,我们将把文献[2]中的结果推广到上半空间或单位球上的调和Bergman-Orlicz 空间中.本文后面如下安排:第二节为一些概念和需要的引理;第三节考虑上半空间上的调和Bergman-Orlicz 空间;第四节给出上半空间上的调和函数差商的有界性;第五节得到单位球上的调和Bergman-Orlicz 空间的Lipschitz 型刻画.在本文中符号表示存在一个正常数C 使得A ≤CB.如果且则记为A ≈B.
2 预备知识
在这一节,介绍一些概念和后面将会用到的引理.
定义H 上的双曲型度量β 为
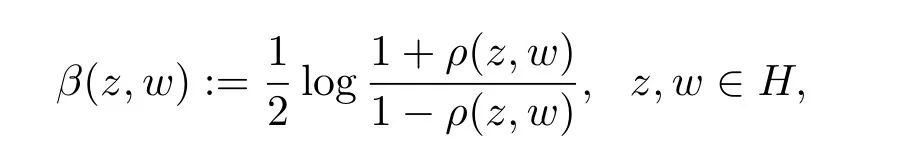
其中
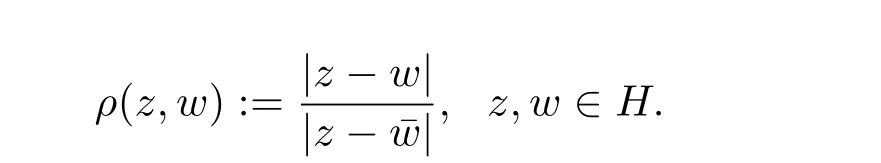
H 上的伪双曲型度量ρ 是平移不变和伸缩不变的,且ρ 是H 上的距离函数,见文献[3]中的引理3.1.
符号Ba(x)表示以a>0 为半径x ∈Rn为中心的欧氏球.对于z ∈H 和r ∈(0,1),设Er(z)表示以r 为半径z 为中心的伪双曲型球.易得Er(z)为欧氏球Ba(x),其中
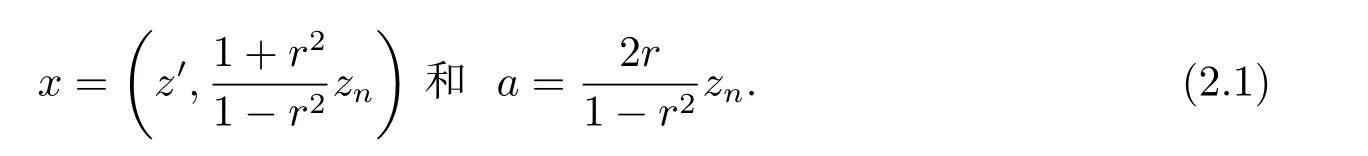
设d(x,Ω)是点x 到集合Ω ⊆Rn上的欧氏距离.则有

引理2.1[3]若z,w ∈H,则

引理2.2[3]若z,w ∈H,则

给定r ∈(0,1),由以上的引理可得

设dw 是Rn上的Lebesgue 测度.以下引理可参考文献[4]中的引理3.5 或者文献[5]中的定理HLFS.

给出多重指标m=(m1,···,mn),其中mi(i=1,···,n)为非负整数,则有|m|=m1+···+mn和其中∂i表示对第i 个指标进行求微分.由引理2.3 和Cauchy 估计得下列引理.其证明可参见文献[6]的推论8.2.
引理2.4[6]设Ω 为Rn中的一个区域.给定1 ≤p<∞和一个多重指标m=(m1,···,mn).则存在一个常数C=C(p,m)>0,使得对Ω 上的任意解析函数f 都有
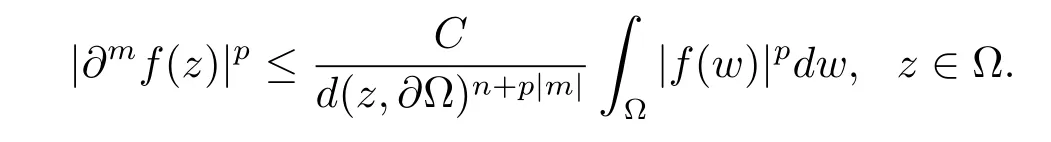
3 上半空间上的调和Bergman-Orlicz 空间
本节的主要定理如下.
定理3.1设α>−1,Φ 是一个增长函数,若则存在一个正的连续函数使得对所有的z,w ∈H,有|f(z)−f(w)|≤ρ(z,w)[g(z)+g(w)].
定理3.2设α>−1,Φ 为增长函数,若则存在一个正的连续函数使得对所有z,w ∈H,有|f(z)−f(w)|≤β(z,w)[g(z)+g(w)].
设p>0,Mp表示存在某个常数C>0 使得对所有的s>0 和t>0,Φ(st)≤CtpΦ(s)成立的凸增长函数Φ 构成的集合.
定理3.3设α>−1,Φ ∈Mp(p>0),若则存在一个正的连续函数使得对所有的z,w ∈H,有|f(z)−f(w)|≤|z −w|[g(z)+g(w)].
引理3.1[7]给定α>−1,则有

对所有z ∈H 成立.
定理3.1 的证明设固定考虑H 中ρ(z,w) 由引理2.2 知 即 令v=w,则 因此存在两个正的常数C1,C2使得同理可得由于对任意的w ∈Er(z),zn≈wn,则当w ∈Er(z)时,有.因此|f(z)−f(w)|≤ρ(z,w)h(z),这里 如果ρ(z,w)>r,则由三角不等式得 伪双曲型距离ρ 满足三角不等式,因此可以选取r'∈(0,1)使得对任意的a ∈Er(z)都有Er(a)⊂Er'(z). 由引理2.4,(2.2),(2.3)式和引理2.2 得 由引理3.1 知 则 运用Φ 的凸性和Jensen 不等式得 在H 上对以上不等式关于dVα(z)求积分且运用Fubini 定理可得 定理3.2 的证明由于ρ ≤β,则定理3.1 中的函数g 也使得该定理成立. 定理3.3 的证明设α>−1,Φ ∈Mp(p>0),若则由定理3.1 的证明知存在一个正的连续函数h 使得对所有的z,w ∈H 有 命题3.1给定α>−1,Φ 为增长函数,则存在一个正常数C 使得对所有f ∈h(H),有 证固定α>−1.假设f ∈h(H)和z ∈H.对于每一个固定的0 则 运用Φ 的凸性和Jensen 不等式得 在H 上对以上不等式关于dVα(z)求积分且运用Fubini定理得 本节考虑H 上关于调和函数的差商.给定f ∈h(H),对所有的z,w ∈H 定义 应用定理3.1 可得以下结果. 定理4.1假设α>−1,Φ ∈Mp,p ∈(α+n,∞)且2γ=p+α −n,则L 有界地映到LΦ(Vγ×Vγ). 证设由定理3.1 知存在一个正的连续函数使得对有 则 故 运用Φ 的凸性,得 因此 在这节考虑Rn上单位球B 上的调和函数.设α 为实数,用vα表示B 上的加权测度,即dvα(x)=(1 −|x|2)αdx.用dvα替代dVα,类似于空间与空间可以定义空间与空间 下列引理由Hardy 等在文献[8]中给出n=2 的证明,n ≥3 的情况见文献[9]. 命题5.1[8,9]给定α>−1 和0 因此有 引理5.1[10]若l,x,y ∈B,则 引理5.2[10]给定α>−1 和实数c,对所有的x ∈B,有 成立. 引理5.3[2]设1 ≤k ≤n,x,y ∈B,y=(x1,···,xk−1,txk,xk+1,···,xn)其中t 是一个标量.则 定理5.1设α>−1,Φ ∈Mp(p>0),f ∈h(B).则下列结果等价. 证(a)(b)类似于定理3.1 的证明可得. 由于[x,y]≥1 −|x||y|≥1 −|x|,1 −|y|.因此 因此得 考虑关于调和函数的差商L 在单位球上的情况.给定f ∈h(B),L 定义为 对于x,y ∈B,由定理5.1 可以模仿定理4.1 的证明,得到在单位球上的类似结果. 定理5.2设α>−1,Φ ∈Mp,n+α 注意到在引理5.2 中c<0 的情况与引理3.1 不同,这个不同可以把上面的调和函数的结果扩展到实单位球上0 定理5.3设α>−1,Φ ∈Mp,0 因此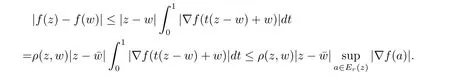
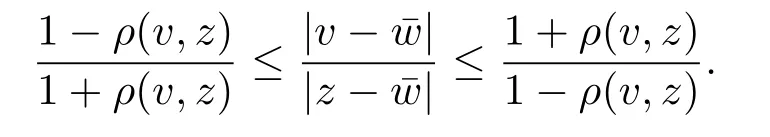

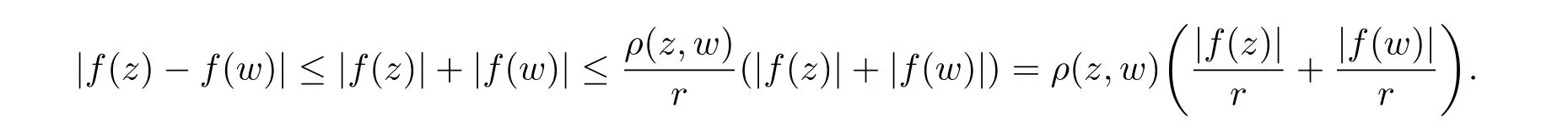
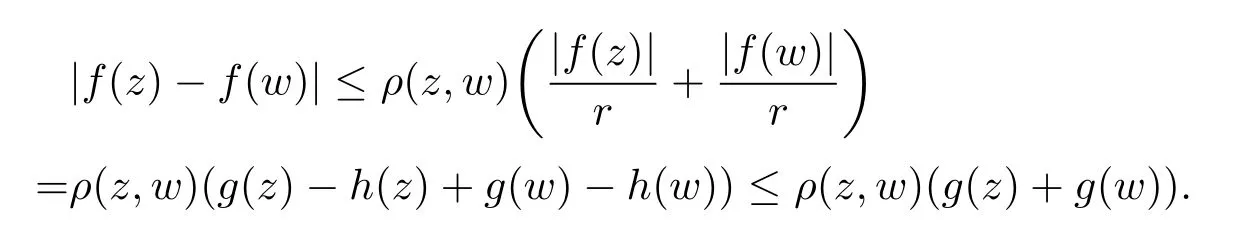
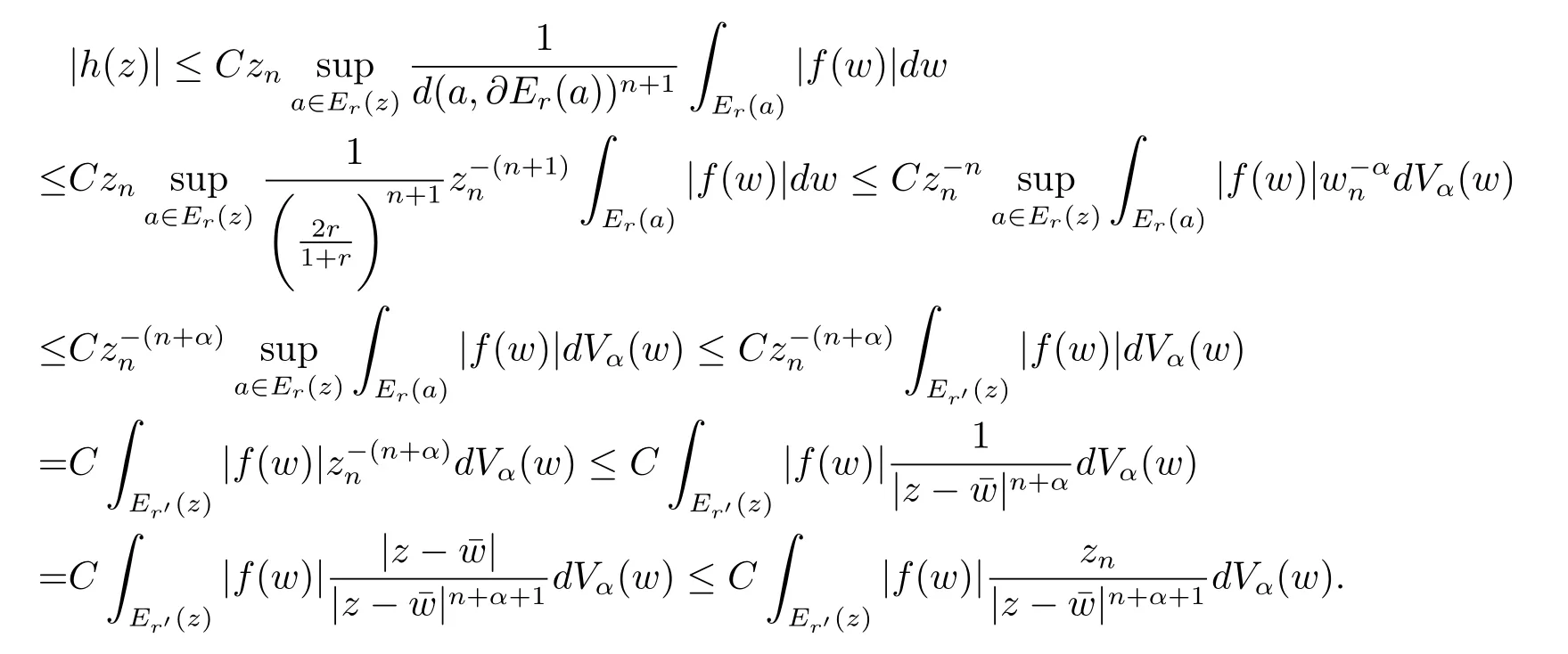


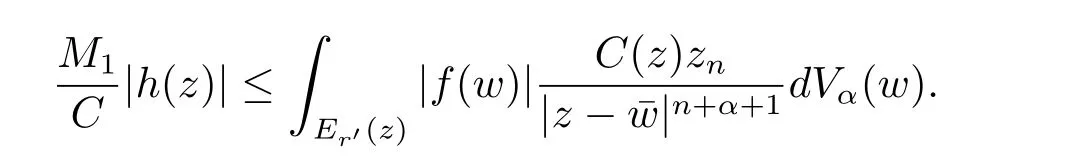
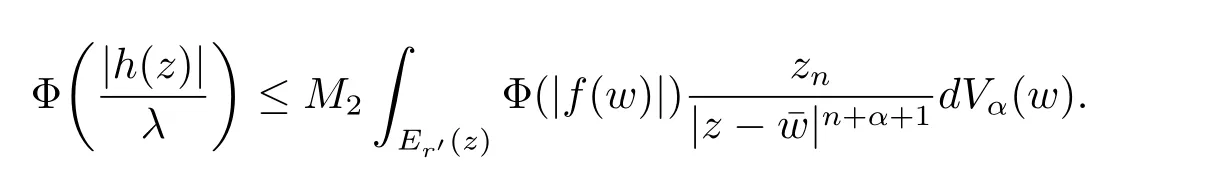
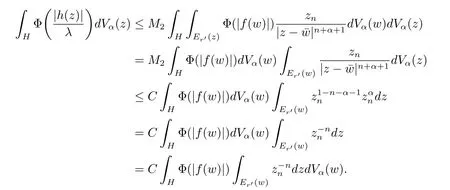
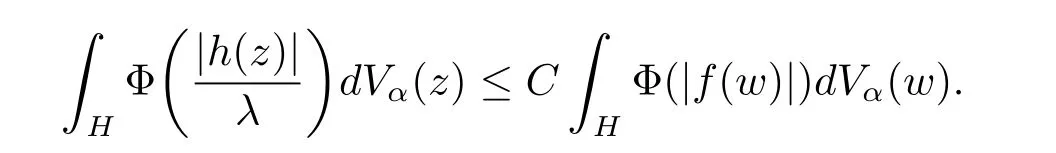
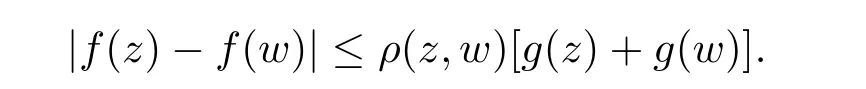

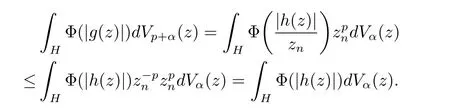


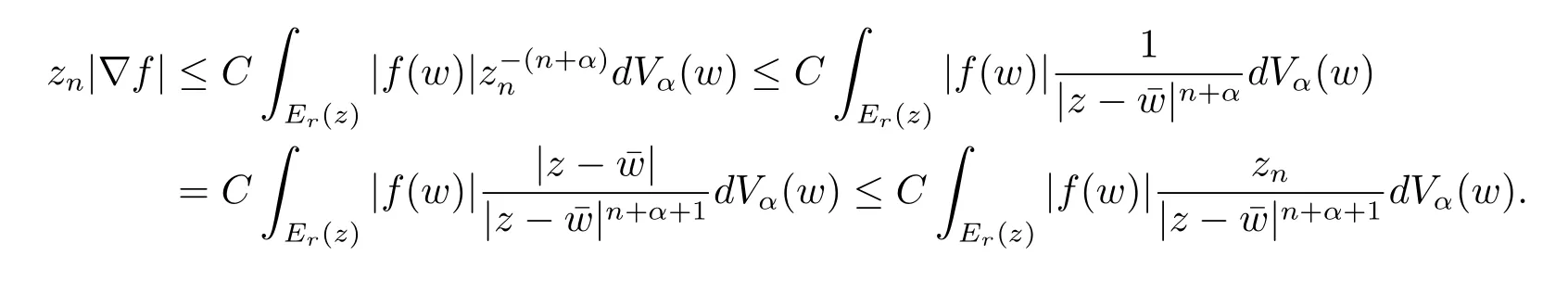
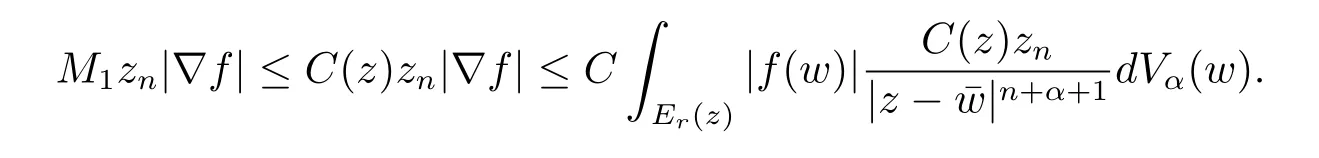
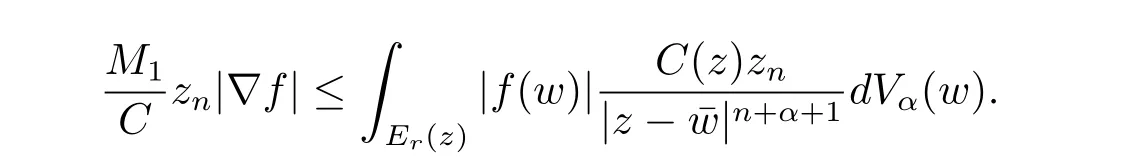

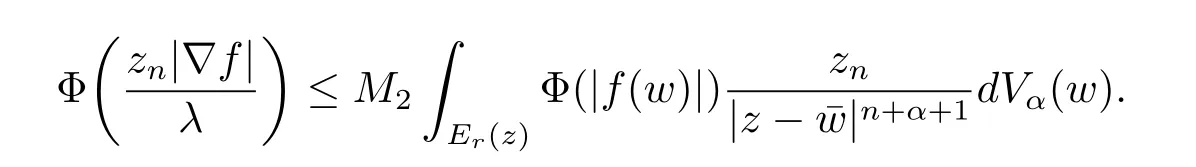

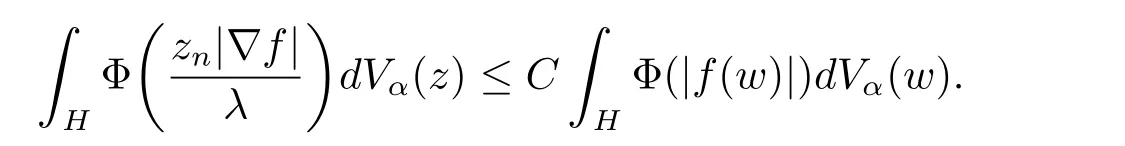
4 上半空间上调和函数的差商



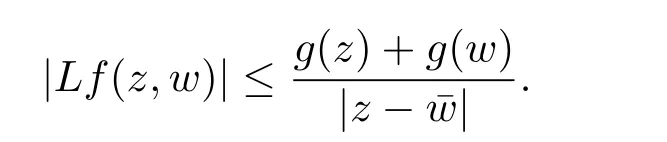
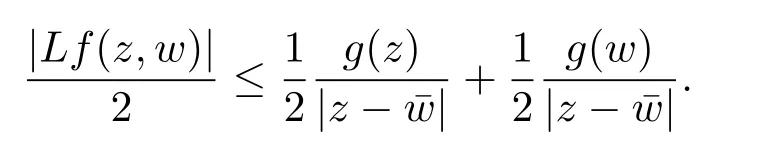

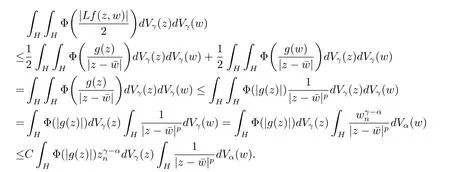
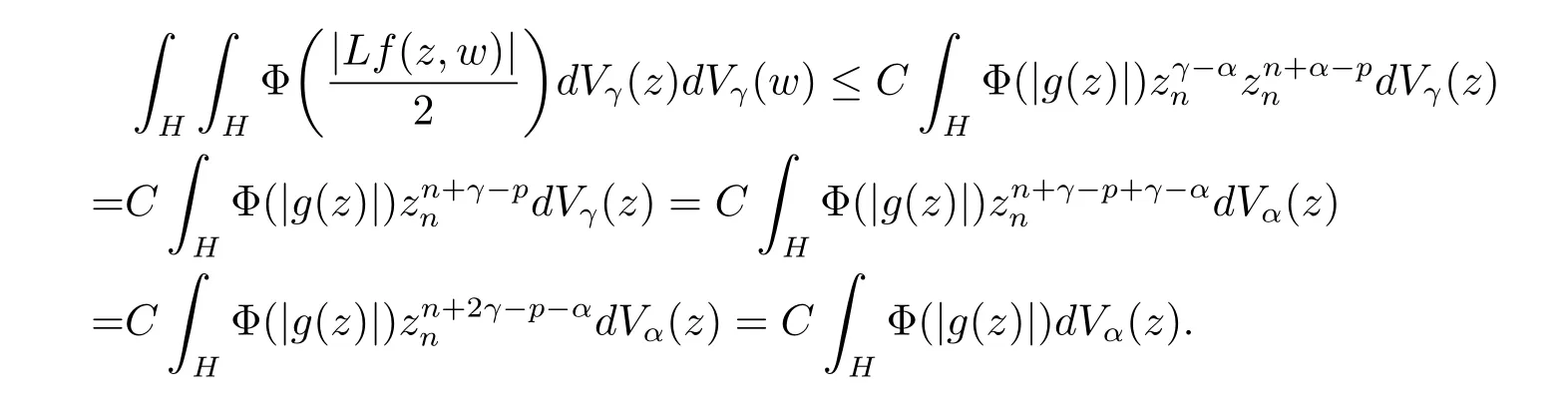

5 单位球上调和Bergman-Orlicz 空间的刻画