孤立子内波存在下的声传播仿真研究
2019-07-31邢传玺刘文博刘佳琪姜思源岳露露
邢传玺,宋 扬,刘文博,刘佳琪,姜思源,崔 琳,岳露露
(1.云南民族大学 电气信息工程学院, 云南 昆明 650500; 2.哈尔滨工程大学 水声技术重点实验室,黑龙江 哈尔滨 150001;3.哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001)
海洋中由于海水密度垂向分布不均匀会导致的海水密度垂直梯度突变,产生密度跃层.此密度跃层内界面,由于水流扰动所引起的波动被称作海洋内波,孤立子内波通常是指其中的非线性大振幅波动.孤立子内波一般是由强度比较大的流通过海底陡坡、海脊等形成的,其形状且和波速在相互碰撞后只有微弱的变化或者保持不变[1-5].
孤立子内波又叫做非线性内波[2],通常具有非线性、大振幅、短周期的特点,经常以3种方式出现,分别为单个孤立波、多个孤立波形成波包、多个波包形成波群,其特征宽度从几百米到几千米、周期为10到30分钟.孤立子内波最常以波群方式传播,其中多个波包间距离可达到几十至一百千米,特征波长最大可达几百千米.由于其在界面处振幅较大,孤立子内波在传播过程中不但会引起海水强烈的垂向混合、影响海洋动植物的生存环境,而且在传播过程中引起海面剧烈辐聚和突发性的强流.孤立子内波又携带巨大的能量,会对水下声呐、海洋工程、海洋捕捞、石油钻井等海面、海底设施构成重大威胁.有研究表明,孤立子内波的传播过程中会产生假潮,对海岸港口会产生极大的破坏性[3-5].
由于孤立子内波在海洋上带来的威胁仅次于台风,国内外学者纷纷开始展开了对孤立子内波的研究.2005年Sugisoto[6]研究了孤立子内波对质量、动量、能量的传递,指出了孤立子内波对声场能量的作用.LUO[7]在2008年,利用射线理论的方法,研究了孤立子内波对声线的聚焦和散焦作用.2009年,Katsnelson Boris[8]研究了浅水孤立子内波存在下声场的时空波动.国内的学者主要研究集中在中国南部海域,2004年,陈守虎[9]等对中国南部海域内波的特点和内波的时空相关性进行了研究,并给出了内波的简正波模态分析结果.刘进忠[10]详细分析了内波对声场传播损失、传播时间、简正波系数等的影响,而且还提出了一种利用简正波群速度来反演孤立子内波的方法,这十分有望应用到孤立子内波检测技术当中.2008年,季桂花[11]等研究了浅海各种内波对匹配场时间相关的影响,提出了内波会使温跃层局部大幅度下降,影响水下设备的检测定位性能.2009年,哈尔滨工程大学的马树青[12]进一步进行了孤立子内波对声场声压传播损失及对其对声源定位的研究.2011年,李整林[13]等进行了孤立子内波存在下简正波到达时间的研究.2015年,周江涛[14]等亚研究了孤立子内波对声场结构的影响.2016年,秦继兴[15]等对浅海能量起伏进行了研究,并对有孤立子内波和没有孤立子内波时进行了对比.
我国拥有广阔的海域和海岸线,在我国沿海有很多浅海地区都存在着海洋内波,随着海洋工程的日益开展,海洋捕捞业的蓬勃发展,海底资源的大力开发,内波尤其是对水面、水底威胁最大的孤立子内波(非线性内波)就越需要去探究.声波是探知海洋、水下定位导航和水下通信的有效载体,建设“数字海洋”,必须要了解、掌握孤立子内波对声传播的影响,因此,本文基于COMSOL有限元方法,对孤立子内波对声传播的影响进行了仿真研究,为孤立子内部的研究提供理论基础和研究依据.
1 孤立子内波建模
1.1 线性内波模型
因为线性内波具有很大的随机性,所以一般用随机场在描述.在不考虑背景流场的情况下,设水体满足密度层化的条件,可知内波的定解方程为[2]:
(1)
其中W为内波水质点垂向运动速度ω的振幅,表达式为ω=W(z)exp[i(σt-kx-ly)];k和l分别为水平坐标(x,y)方向上的波数,且χ2=k2+l2;σ表示频率,t为时间,g为重力加速度,f为科氏参数,β=df/dy;H为不变值海洋深度,N为浮力频率表达式为:
(2)
引入f-平面近似,即取β=0,且设l=0,则有:
(3)

海洋中常见的内波波长一般都不超过1 km,因此f-平面近似可以成立[2].
然后,设海面是没有波动和起伏的,W(0)=0, 引入“刚盖近似”:
(4)
W(-H)=0,W(0)=0.
再进一步引入Boussinesq近似,内波方程可进一步的简化为:
(5)
W(-H)=0,W(0)=0.
这就是Fjelsted内波方程.
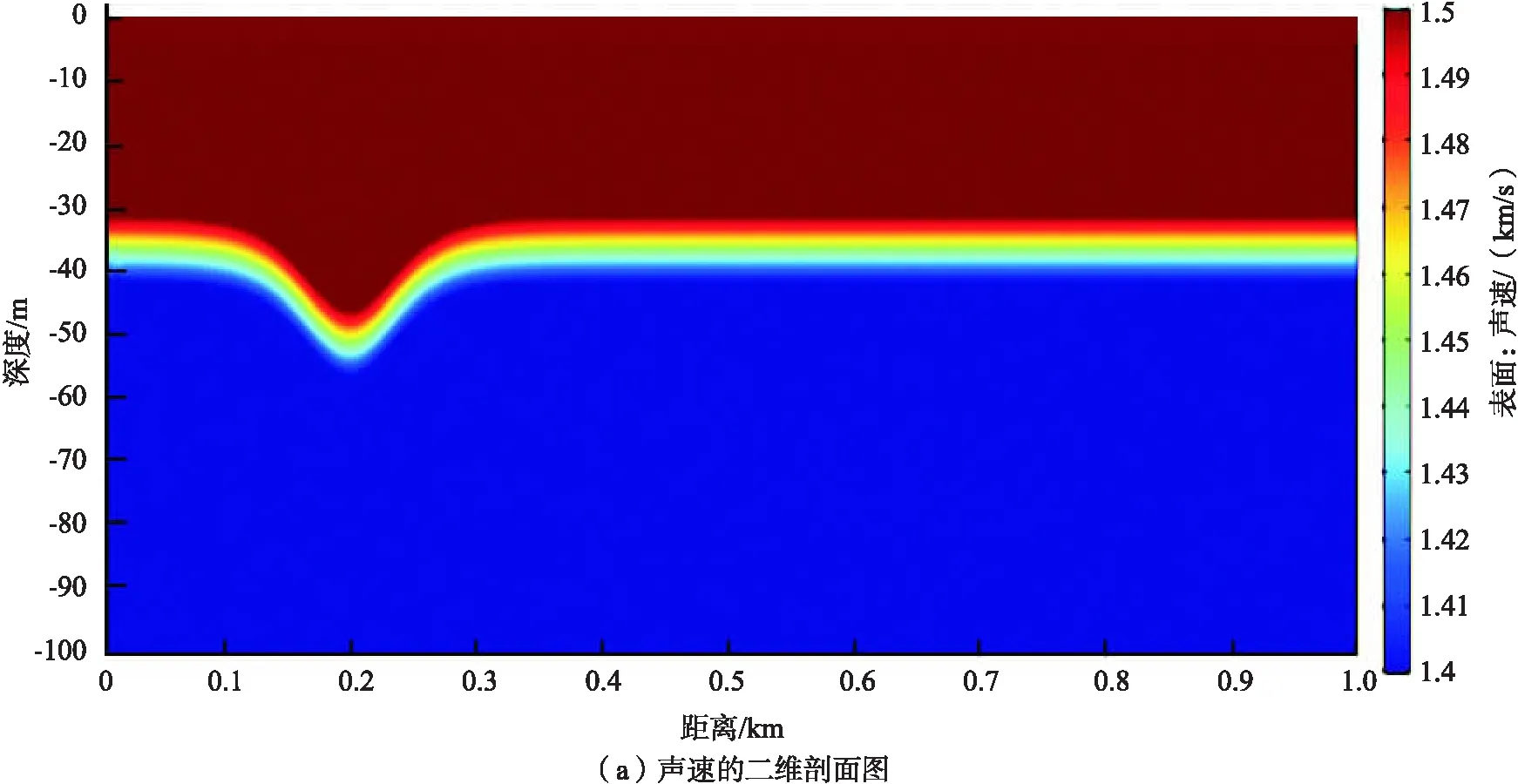
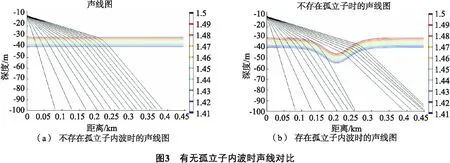
若忽略地转效应使f=0,且满足大尺度波动的情况下,或者当f2<<σ2< (6) W(-H)=0,W(0)=0, 其中c=σ/k为波动的相速度. 通常情况下,可通过KdV方程来求解方程的孤立子解[3]. 如果KdV方程的形式如下: θt-6θθx+θxxx=0, (7) 其中θ为KdV方程的孤立子解,θt为其对时间t的一阶偏导,θx为其对位移x的一阶偏导,θxxx为其对位移x的三阶偏导. 设θ(t,x)=f(u),其中u=x-ct,代入公式(7)后求解可得孤立子解: (8) 如果不考虑地转影响,引入Boussinesq近似可得到KdV方程的标准形式,求解之得到孤立子解.不同孤立子内波模型的KdV方程可得到不同的孤立子内波解.本文使用的模型为如图1所示, 此模型下,孤立子内波的垂向位移为: (9) 公式9的模型适用于实际的海洋环境,由n个孤立子内波组成的模型,其中的W(kh,j)为简正波的模态函数,Λm为孤立子内波的振幅,Vm为其移动速度,Δm为孤立子内波的波包宽度. 孤立子内波会改变海水的声速,海水声速的变化会使声线轨迹发生变化,最后可通过声线轨迹的改变来反映孤立子内波对二维声场的影响. 设孤立子内波的振幅15 m,波包宽度为50 m,在距声源水平距离200 m处出现其振幅的极大值: (10) 为了便于观察设置海水为温跃层浅海,海水深度为100 m,海面视为绝对软边界,海底视为绝对硬边界,海水中存在负声速梯度,图2为存在孤立子内波时的海水声速分布. 利用存在孤立子内波时的声速分布进行声线轨迹仿真,设声场中存在一点声源,声源位于10 m处,声源频率为100 Hz.在COMSOL中把物理场设为射线声学,研究设为声线轨迹,仿真得到有无孤立子内波时声线轨迹图如图3所示,为便于讨论孤立子内波对声线轨迹的影响,仿真中省略了海底反射等因素. 从图3中可以看出,孤立子内波可以明显的改变声线的传播轨迹,水平200~400 m区域是孤立子内波影响的主要区域,其声线轨迹变得稀疏,400 m后的声线轨迹则变得十分密集.可近似的认为孤立子内波使200~400 m区域的能量减少,使400 m后区域能量增加. 设声源深度10 m,接收深度10 m,分别计算当声源发射频率为50 Hz、100 Hz、150 Hz、200 Hz时的传播损失,其中声源频率为50 Hz和250 Hz时的计算结果如图4所示.从图4可知,声源频率为50 Hz时,孤立子内波对声信号的传播没有特别大的影响,这是因为低频声波激发的简正波模态相对较少,孤立子内波对各阶简正波的耦合没有产生太大的影响,声波对孤立子内波产生了饶射,所以内波只对声传播产生了微小的影响,并没有对声场干涉结构有很大的改变.随着声源频率从50 Hz升到250 Hz,孤立子内波对声压传播损失的影响逐渐加大.当声源频率f=250 Hz时,声压传播损失会因为孤立子内波的存在急剧增加,对水平距离2 700 m后的传播损失都产生了较大的影响. 孤立子内波会改变声场的干涉结构,进而引起声压传播损失的起伏幅度和位置的变化,在不同距离处的声压传播损失也会有起伏.仿真得到在不同声源发射频率下,存在孤立子内波时的声压传播损失与无内波时的传播损失差值如图5所示: 在声压传播损失差值较大的声源发射频率,可以近似认为孤立子内波与声波产生了共鸣现象.通过仿真分析可知,一般在声源频率低于70 Hz时,孤立子内波对声传播影响较小,随着频率的升高其影响逐渐加大并波动起伏. 为了更好研究孤立子内波对声传播的影响,将声源深度和接收深度分别设置为10 m、20 m、30 m,其他环境参数不变,发射信号频率为250 Hz,仿真计算得到声源深度10 m,分别计算不同声源和接收深度下有孤立子内波时声压传播损失减去无内波时声压传播损失差值如表1、2、3所示. 表1 声源深度10 m时不同接收深度和水平距离处声压传播损失差值 dB 表2 声源深度20 m时不同接收深度和水平距离处声压传播损失差值 dB 表3 声源深度30 m时不同接收深度和水平距离处声压传播损失差值 dB 对仿真结果进行分析可知: 1)当声源位于海底深度10 m时,有内波影响的情况下,在接收深度10 m处的传播损失增加了8 dB以上,在跃层处的传播损失增加了2 dB,而跃层的下方,深度30 m处的传播损失减少了11 dB.这种情况产生的原因是因为声源在跃层的上方,能量集中在这一部分,孤立子内波使声波产生散射和折射,造成其传播损失增加. 2)当声源位于海底深度30 m时,跃层上方的传播损失减少了6 dB以上,跃层处的传播损失变化不是很明显,跃层下方增加了1.7 dB左右.这种情况产生的原因是此时声源能量集中在下层,孤立子内波使跃层下方的传播损失增加. 3)当声源位于海底深度20 m时,跃层上方的传播损失增加了12 dB,下方减少了13 dB,跃层处的传播损失增加了2 dB.这是因为孤立子内波就位于跃层附近,此时孤立子内波对传播损失影响较小. 由仿真分析可知,孤立子内波使声传播产生散射,并改变声场的能量分布.孤立子内波会使声场的干涉结构更复杂. 在低频时,孤立子内波对声场的作用较小,设声源发射信号频率为250 Hz,环境参数不变,声源深度为30 m,接收深度为10 m,仿真计算得到孤立子内波影响下声压、质点振速和声能流传播损失对比如图6所示. 通过图6(b)、(c)看出,孤立子内波会使水平质点振速传播损失减小,使垂向质点振速略微增加.从图6(d)、(e)可看出孤立子内波使水平、垂向声能流密度传播损失减少. 基于COMSOL软件进行仿真,建立孤立子内波模型,通过仿真研究分析了孤立子内波对声传播产生的影响.研究结果表示,孤立子内波对声线具有折射作用,声线发生了偏折,使声线密集程度、声波到达时间、声场能量分布等都发生了改变.孤立子内波对声压传播损失和声场干涉影响的研究发现,孤立子内波对声场能量有明显的改变.浅海的情况下,孤立子内波对声传播的影响与声波频率有关,低频声波的简正波模态较少,对孤立子内波产生绕射作用,使孤立子内波对声场的影响很小;声源位于跃层上、下方时,孤立子内波使跃层上、下方的声压传播损失产生了明显的变化.而在声源位于跃层时,传播损失并没有很大的变化.孤立子内波对声波有一定的散射作用,可使声场能量分布更均匀. 对声矢量场进行的仿真研究发现,孤立子内波会使声场能量小处水平振速的传播损失减小,使垂直振速的传播损失略微增加.在实际应用中,可采用声压信号联合处理等方法来减少孤立子内波对声传播的影响.1.2 孤立子内波模型


2 孤立子内波对声线轨迹的影响仿真
2.1 孤立子内波对海水声速梯度的影响仿真

2.2 孤立子内波对声线轨迹的影响仿真研究
3 孤立子内波对声场的影响仿真
3.1 声源频率不同时孤立子内波对声传播的影响仿真
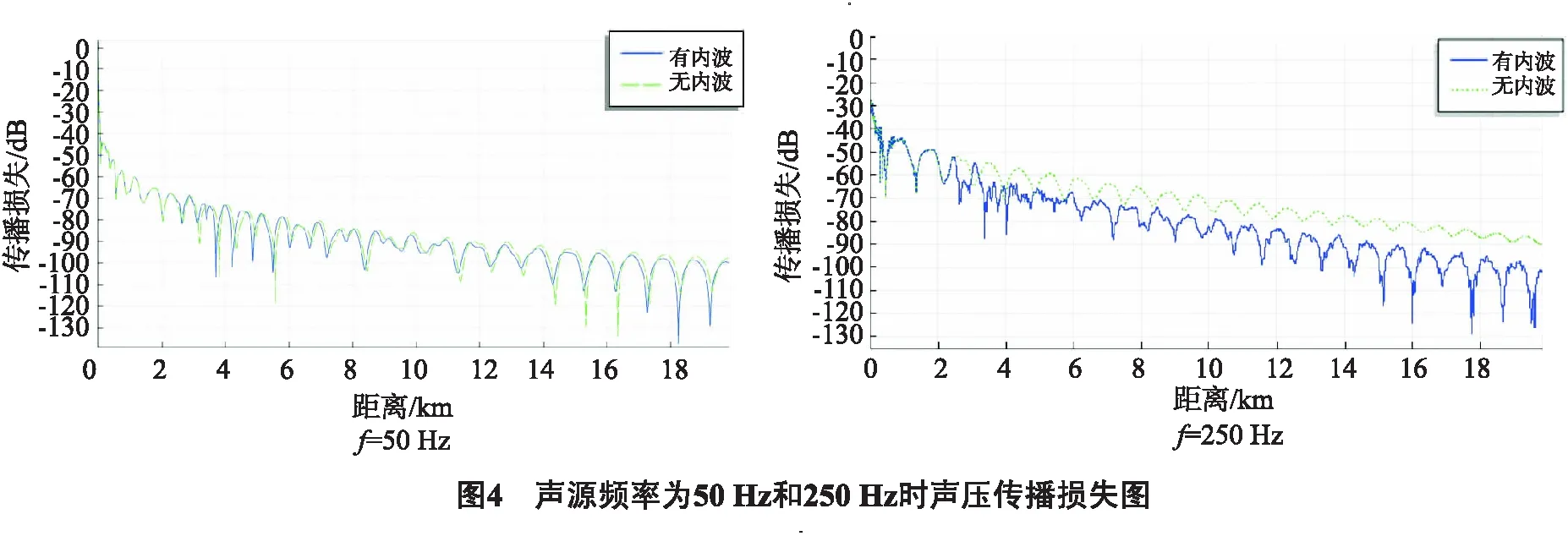
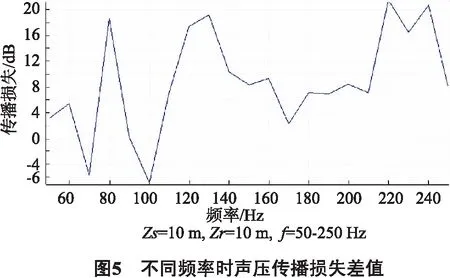
3.2 声源深度与接收深度不同时孤立子内波对声传播的影响仿真



3.3 孤立子内波对声矢量场的影响仿真研究


4 结语
