病毒在鸟和鸟之间传播对西尼罗河热传播的影响*

曹玲玲， 宋海涛

(1.山西大学 复杂系统研究所，山西 太原 030006；2.山西大学 数学科学学院，山西 太原 030006； 3.山西大学 疾病防控的数学技术与大数据分析山西省重点实验室，山西 太原 030006)

西尼罗河热是一种由西尼罗河病毒引起的媒介疾病,1937年该病毒首次从乌干达西尼罗河流域一名发热妇女的血液中分离出来[1].最初,这种疾病没有引起人们的注意.直到1957年,以色列西尼罗河病毒性脑膜炎流行后人们才认识到这种病毒的危害[2],20世纪60、70 年代西尼罗河病毒感染相继在法国和南非流行[3],90年代以来该病在亚洲、欧洲和非洲广泛流行造成大量的人员伤亡和严重的经济损失[4],引起了全世界的广泛关注.

西尼罗河病毒通过雌性蚊子叮咬传播给人类和其他动物,雌性蚊子从感染病毒的鸟类的血液中获取该病毒.蚊子是西尼罗河病毒传播的载体,例如埃及伊蚊、 库蚊和疟蚊等.鸟是西尼罗河病毒的天然宿主[4].当携带病毒的雌性蚊子叮咬一只易感的鸟,这时易感鸟有感染病毒的风险.鸟类在感染后的一到四天内血液中维持着相当高的病毒滴度水平,感染病毒的鸟可能会把病毒传染给叮咬它的易感蚊子.病毒就这样在自然界保持蚊子-鸟-蚊子的传播循环[5].

关于西尼罗河病毒传播动力学模型分析已经有很多研究,例如文献[6]、[7]和[8]等,但是在这些研究中都没有考虑西尼罗河病毒在宿主鸟之间的传播.文献[9]和[10]研究表明西尼罗河病毒可能会在鸟和鸟之间传播,病毒在宿主鸟之间的传播实际上可以增加病毒的存活率,进一步影响疾病的流行,因此在接下来的工作中有必要考虑病毒在宿主之间的传播对疾病传播的影响.

本文基于西尼罗河病毒在蚊子和鸟的传播循环建立了一个关于媒介蚊子和宿主鸟的常微分方程模型,考虑病毒在宿主之间的传播对西尼罗河热疾病传播的影响.首先计算了基本再生数R0,通过构造Lyapunov函数证明了当R0≤1时,无病平衡点E0是全局渐近稳定的；当R0>1时,正平衡点E*是全局渐近稳定的.在数值模拟部分模拟了病毒在宿主鸟之间的传播对感染类(蚊子和鸟)的影响.

1 模 型

假设Ms和Mi分别表示易感和感染的成年雌性蚊子的数量.Bs、Bi和Br分别表示易感、感染和恢复健康的鸟的数量.全部雌性蚊子的总量表示为Nm=Ms+Mi,全部鸟的总量表示为NB=Bs+Bi+Br，假设Nm和NB是常数.成年雌性蚊子出生率表示为Λv,宿主鸟的出生率表示为Λh,μv表示雌性蚊子的自然死亡率.鸟和蚊子之间的交叉感染通过鸟的标准群体性行为模拟[11].β1v和β1分别表示感染鸟对易感蚊子和感染蚊子对易感鸟的有效接触率,β2表示感染鸟对易感鸟的有效接触率,αh表示感染鸟的康复率,μh表示鸟的自然死亡率,基于以上的假设建立以下模型

(1)

令

由于模型(1)的前四个方程中不含有Br(t),下面只考虑由前四个方程构成的系统

(2)

系统中所有的参数都是非负的,区域D={(Ms(t),Mi(t),Bs(t),Bi(t))|Ms(t),Mi(t)Bs(t),Bi(t)≥0}是系统(2)的正向不变集.

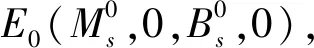
根据文献[12]中的下一代矩阵方法可以计算出基本再生数R0,

因此

则

其中ρ(FV-1)表示矩阵FV-1的谱半径.

2 模型的全局动力学

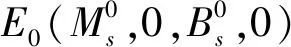
证明容易得出在E0处的特征方程为

特征方程有两个根λ1=-μh<0,λ2=-μv<0.

当R0<1时,易得λ3+λ4<0,λ3λ4>0

综上所述，在E0点处的特征方程的所有特征根都具有负实部,因此E0是局部渐近稳定的.

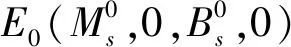
证明设函数f(x)=x-1-lnx≥0,x>0.取Lyapunov函数

函数V0(t)的导数为

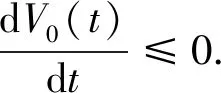
首先令系统(2)的右边为零,可得

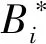
(3)

其中

h0=(μh+αh)μvβvβh2>0

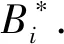
推论2 当R0>1时,系统(2)的正平衡点E*是局部渐近稳定的.

证明令

在点E*处的特征方程是

整理得

(4)

方程(4)的两边同时除以λ+μh得,

假设λ(Reλ≥0)是方程(4)的根,则

定理2 当R0>1时,系统(2)正平衡点E*是全局渐近稳定的.

证明取Lyapunov函数为

函数V1(t)的导数为

3 数值模拟

现通过数值模拟验证前面所述的理论结果并描绘有效接触率βh2对感染类(蚊子和鸟)的影响.

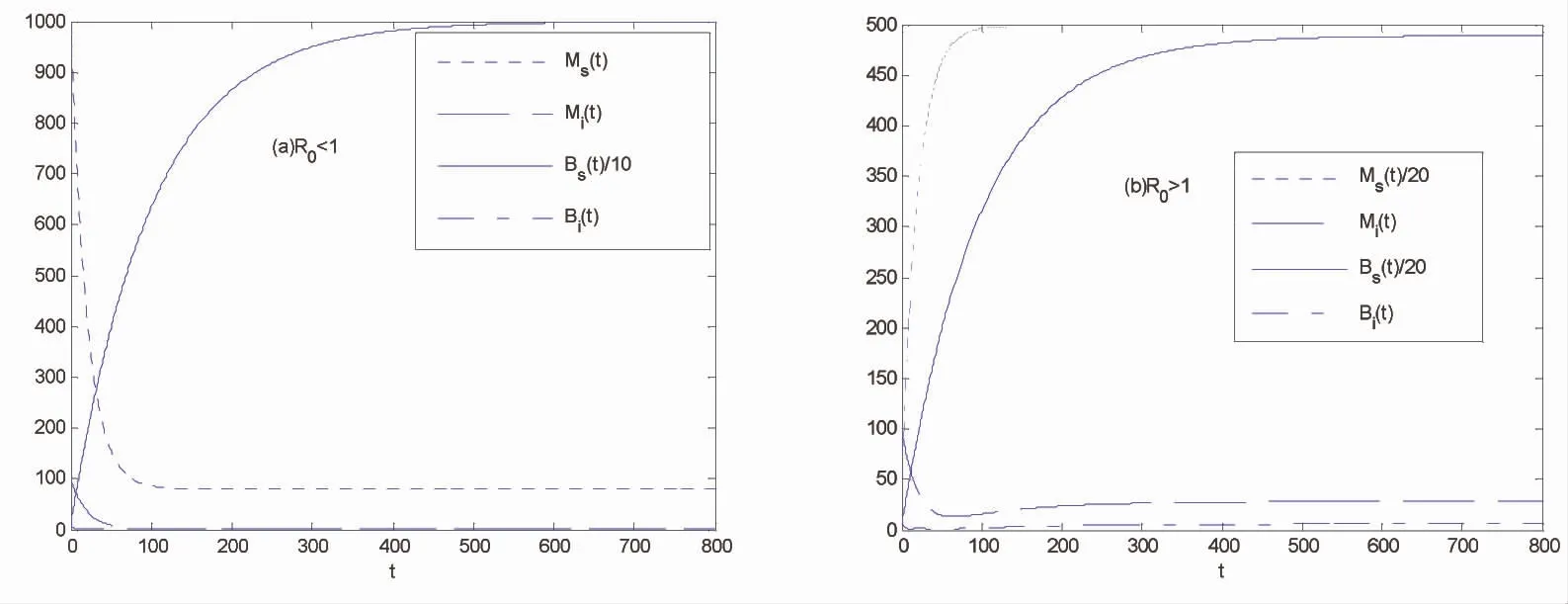
图1 当R0<1和R0>1时，系统(2)的解是渐近稳定的Fig.1 The solutions of the system (2) are asymptotically stable when R0<1 and R0>1

根据文献[5]和[14],图1(a)中分别取参数Λv=4,Λh=100,βv=0.000 144,βh1=0.08,βh2=0.001,μv=0.05,μh=0.01,αh=0.36,在图1(b)中取参数Λv=500,Λh=100,其他参数和图1(a)一样.图1描绘了当R0=0.790 5<1时,系统(2)的无病平衡点是全局渐近稳定的,当R0=8.823 9>1时,系统(2)的正平衡点是全局渐近稳定的.

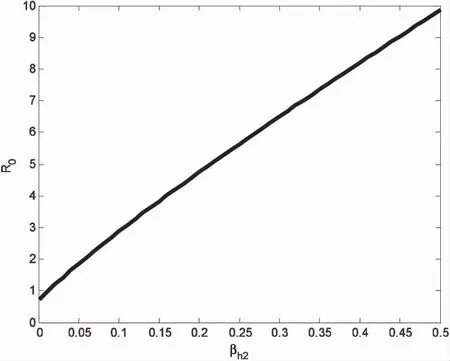
图2 R0和βh2的关系Fig.2 The relationship betweenR0 and βh2

图2描绘了有效接触率βh2对R0的影响,βh2增加,R0也会增加,只有当βh2特别小时才会使R0<1,其他参数和图1(a)一样.

由图3可以清楚的知道病毒在宿主之间传播的有效接触率βh2对感染类有不同的影响,注意到βh2从0.01增加到0.08时,从图3(a)看到感染蚊子的数量降低,从图3(b)易知感染鸟的峰值数量增加,其他参数和图1(a)一样.

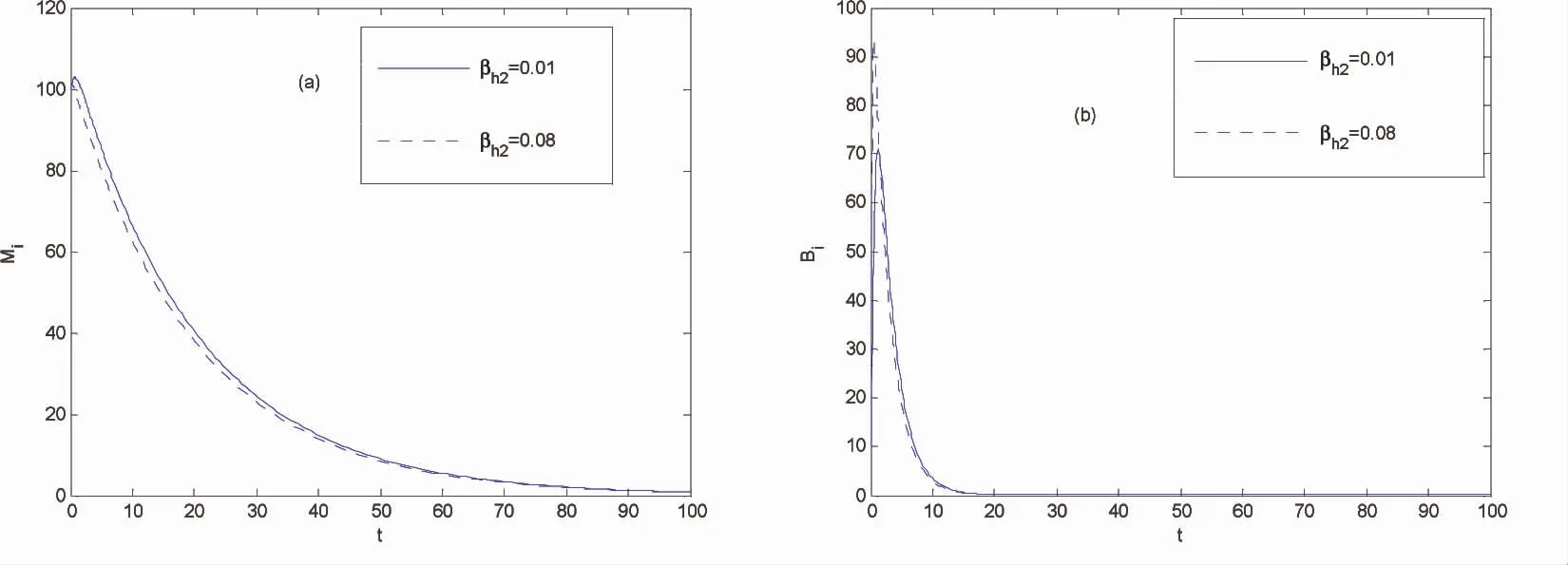
图3 βh2对感染类(蚊子和鸟)的影响Fig.3 The effect of βh2 on infectious species(mosquitoes and bird)

4 总 结

20世纪90年代以来,西尼罗河热在亚洲、欧洲、非洲广泛流行造成大量的人员伤亡和严重的经济损失,因此考察研究影响疾病流行的因素十分必要.本文建立了西尼罗河病毒在蚊鸟种群中传播的常微分方程模型,考虑病毒在宿主鸟之间的有效接触率对西尼罗河疾病流行的影响.计算了基本再生数R0,证明了当R0≤1时,系统(2)的无病平衡点是全局渐近稳定的,当R0>1时,系统(2)的正平衡点是全局渐近稳定的.由数值模拟部分可以看出当βh2增加时,R0也会增加,只有当βh2特别小时才会使R0<1.有效接触率βh2对感染类有不同的影响,当βh2变大时,感染蚊子数量降低,但是感染鸟的峰值数量增加.