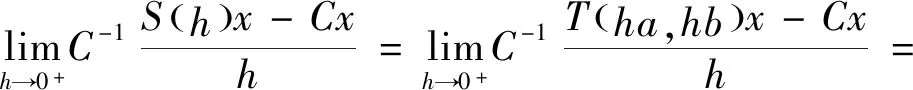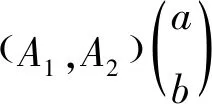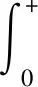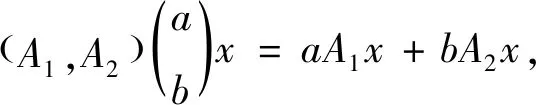双参数n阶α次积分C半群的逼近*

赵丹丹,赵华新

(延安大学 数学与计算机科学学院, 陕西 延安 716000)

自Hille[1]首先提出算子半群理论以来，其理论得到不断丰富和发展.文献[2]中Pazy建立了压缩C0半群的Hill-Yosida定理.徐敏等[3]从双参数C半群的无穷小生成元的Yosida逼近出发，给出了两个充要条件.仓定帮等人[4]引入了Banach空间上双参数算子半群生成元的Yosida逼近的定义；徐敏[5]给出了双参数C半群的Yosida逼近定理及逼近的相关性质.张明翠[6]给出了单参数n阶α次积分C半群的概念并讨论其相关问题.本文在上述研究的基础上将单参数n阶α次积分C半群推广到双参数n阶α次积分C半群，给出了双参数n阶α次积分C半群无穷小生成元的定义，并讨论其逼近定理.

1 预备知识

在本文中，X为无限维的复Banach空间，B(X)是X上有界线性算子全体所成的Banach代数；D(A)为线性算子A的定义域，设n∈N，α≥0.

JnT(t)表示T∈C([0,+),X)的n次积分，即

T=0当且仅当存在n>0使JnT(t)=0,t≥0.

2 双参数n阶α次积分C半群的定义

定义1 设n∈N，α≥0，C∈B(X)是单射, {T(t,s)}s,t≥0⊂B(X)强连续，若存在算子A=(A1，A2)使

(2)CT(t,s)=T(0,s)T(t,0)

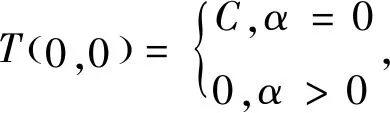
定义2 双参数n阶α次积分C半群{T(t,s)}t,s≥0的无穷小生成元是C-1与T(t,s)在(0,0)处的微分的积，记为A=(A1,A2)，且A1、A2分别为单参数n阶α次积分C半群的无穷小生成元，即

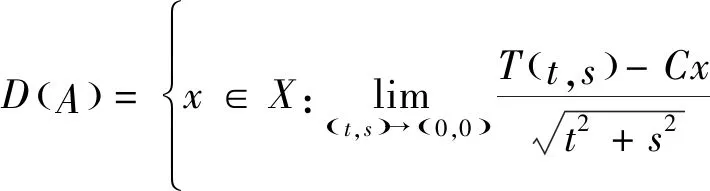
3 主要结论

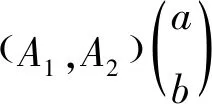
证明设 {T(t,s)}t,s≥0是双参数n阶α次积分C半群，则{T(t,0)}t≥0和{T(0，s)}s≥0是两个单参数n阶α次积分C半群，则它们的无穷小生成元A1、A2在X上是闭的，令u=(a,b)∈R×R，则：

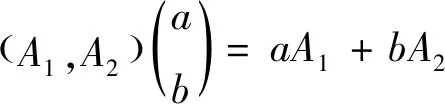
定理2 设{T(t,s)}t,s≥0是双参数n阶α次积分C半群，有x∈X,则有

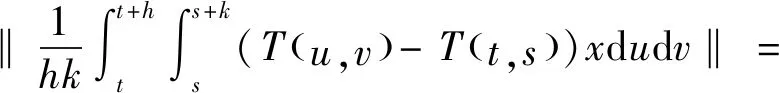
当(h,k,δ1,δ2→0)时，T(0，0)=C.定理得证.

下面给出双参数n阶α次积分C半群Yosida逼近定理.

定理3A=(A1，A2)为双参数n阶α次积分C半群{T(t,s)}t,s≥0的无穷小生成元，当且仅当：

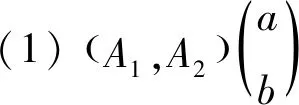
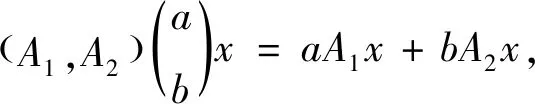
U=(a,b)∈R×R,S(h)=T(hu)=T(ha,hb)