法丛平坦子流形的余维数限定*

马赛飞，郭震，王爱蕊

(云南师范大学 数学学院，云南 昆明 650500)

1 引 言

设x:Mn→Nn+p是n维黎曼流形Mn到n+p维黎曼流形Nn+p的等距浸入，其中p称为余维数，当Mn和余维数p满足一定条件时，Mn可等距嵌入到一个欧氏空间中作为子流形，这是与子流形余维数相关的问题，一直以来受到了很多数学家的关注[1].根据Nash的嵌入定理[2]，可知每个黎曼流形可以等距嵌入到维数足够高的欧氏空间中,因此自然就提出一个问题：能否寻找一个维数足够低的欧氏空间，使得一个黎曼流形能够嵌入到这个欧氏空间中去,对此问题前人做了大量的研究.

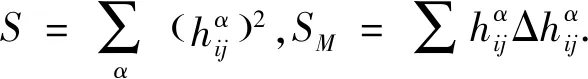
本文研究法丛平坦子流形的余维数，考虑当黎曼流形Nn+p为具有常截曲率c的空间形式的情况，记为Nn+p(c),得到如下定理.

定理1 设x:Mn→Nn+p(c)(p≥2)是n维黎曼流形Mn到n+p维空间形式Nn+p(c)的等距浸入子流形，若Mn的法丛平坦，则余维数不超过子流形的维数，即p≤n.

2 记号、定义和基本公式

Nn+p(c)是具有标准度量〈·,·〉的n+p维常曲率为c的空间形式，Mn是该空间形式中具有平坦法丛的子流形.在Nn+p(c)上选取局部正交标架场{eA},{ωA}为其对偶标架，使其限制在Mn上有{ei}切于Mn,{eα}法于Mn,且有如下指标约定：

1≤A,B,C，…≤n+p,1≤i,j,k,l,…≤n,n+1≤α,β,γ,…≤n+p

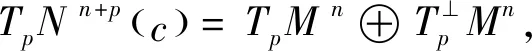
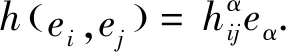
Nn+p(c)在基底下的结构方程为:

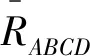
(1)

Rαβij=0,ωαβ=0

(2)

空间形式Nn+p(c)的子流形的结构方程为：

上述方程可积条件为：

又由(2)式的第一式有

(3)

3 定理的证明

证明定理前先证如下命题.

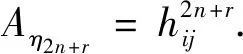
证明由题设条件R⊥=0及(3)式有

(4)

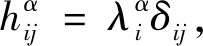
对法标架场en+1,…,e2n作法标架变换有：

(5)

由矩阵秩的性质，有rankB≤min(n，p),其中rankB为矩阵B的秩.若p>n,则有rankB≤n,由此可对矩阵B的秩进行分类讨论.

(6)

设

并结合(5)式和(6)式有

(7)

由(7)式有

同理有Aη2n+1=……=Aη2n+r=0.

Case2：rankB

定理1的证明取ηn+1,…,η2n,η2n+1,…,ηn+p(p>n)为Mn的法标架场，则由(2)式和定理条件并结合命题1有x:Mn→Nn+p(c)在此标架下的结构方程为：

(8)

由(8)式有

d(η2n+1Λ…Ληn+p)=0

(9)

由(9)式容易得出p-n个矢量外积η2n+1Λ…Ληn+p在Mn上为常量，因此，子流形Mn包含于一个线性空间ν,且ν⊥=span{η2n+1,…,ηn+p}≅Np-n为p-n维固定子空间，从而Mn含于N2n中作为子流形，由此定理得证.