德西特空间中常平均曲率类空超曲面的全测地性*

王琪

(贵阳学院 数学与信息科学学院，贵州 贵阳550005)

1 引 言

de Sitter 空间是数学界和物理学界共同关注的一种非平坦伪黎曼空间形式，它是有常数截面曲率的连通伪黎曼流形.就n+1维单位de Sitter空间 dSn+1而言，其截面曲率K≡1.

几十年来，人们对dSn+1中具有常数平均曲率的类空超曲面，作了大量研究，得到许多结果[1-7].关于3维单位de Sitter 空间 dS3中有常数平均曲率的类空超曲面，文[1] 曾经给出一个结果，即下列定理1.利用文献[1-3] 给出的一个关于超曲面的第二基本形式模长平方S的 拉普拉斯ΔS的一个估计公式，本文得到一个新的定理，即下列定理2.定理2改进了定理1的结论.

定理1[1]设M是3维单位de Sitter空间dS3中的紧致无边的类空超曲面.如果M的平均曲率H为常数，则必有H2<1.

定理2 设M是n+1维单位de Sitter空间 dSn+1中的紧致无边的类空超曲面.如果M的平均曲率H为常数，则必有：M的第二基本形式模长平方S≡H≡0，即M必为全测地超曲面.

2 准备知识

记Rn+2为n+2维欧氏空间，并令Rn+2带有负指标为1的 Lorentz 度量[1-6]，即

〈,〉=-(dx1)2+(dx2)2+…+(dxn+2)2

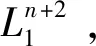
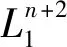
并令其带有诱导度量，则dSn+1是连通的伪黎曼空间，且其截面曲率K≡1.

令(M,g)为黎曼流形，而φ:M→dSn+1是光滑流形间的浸入映照.如果g=φ*(〈,〉),则M或者φ(M)称为dSn+1中的类空等距浸入超曲面，其中〈，〉是dSn+1中的 Lorentz 度量.

以下规定指标取值范围为

1≤i,j≤n,0≤α,β≤n

同时，记矩阵

其中δij是标准 Kronecker 张量.

设e0,e1,…,en是与dSn+1的伪黎曼度量相适应的局部标架场，又设ω0,ω1,…,ωn是与dSn+1的伪黎曼度量相容的对偶标架，即

其中δαβ也是标准 Kronecker 张量.

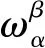
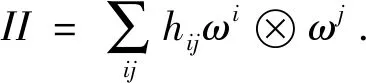
M的平均曲率定义为[1-4]

且平均曲率的定义与局部标架场e0,e1,…,en的选取无关.

定义M的第二基本形式的模长平方为[1-7]

且S的定义与局部标架场e0,e1,…,en的选取无关.

3 定理2的证明

证明由Cauchy-Schwartz不等式，有

(1)

用ΔS表示S的拉普拉斯.当M的平均曲率H为常数时，参照文[1-3] 的计算，有

(2)

首先，假设常数平均曲率H≠0. 此时，通过适当选取M的类时单位法向量场的指向(过去指向或者将来指向)，可以假设常数平均曲率H<0， 再结合 (1) 式，则由 (2) 式有

(3)

因为M是紧致无边的，由 Hopf原理，以及 (3) 式，可知S在M上为常数.再由 (3) 式知道：S≡0，从而由 (1) 式有：H≡0，但这与H≠0的假设矛盾，这个矛盾说明：在M上必须有H≡0.

由H≡0及(2) 式又有

(4)

同样因为M是紧致无边的，由 Hopf原理以及 (4) 式知道：S在M上为常数.又因为S在M上为常数，再由 (4) 式并结合 (1) 式知道:S≡0. 证毕