与三个数论函数有关的一类复合方程的可解性*

张明丽,高丽

(延安大学 数学与计算机科学学院，陕西 延安 716000)

1 引 理

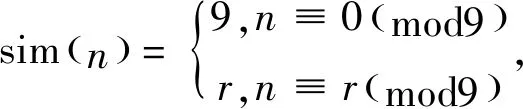
引理2[5-9]：对于任意的整数n,设p是素数，定义p的原数函数为最小的正整数为m,使得pn|m!,即Sp(n)=min{m:pn|m!}.

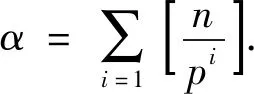
引理5[10]：对任意素数p≥3,Z(p)=p-1.

引理6[10]：对任意素数p≥3及k∈N+,Z(pk)=pk-1.当p=2时，有Z(2k)=2k+1-1.

2 主要结论及其证明

定理1：对于任意的正整数n,混合函数方程Z(n)=S2(sim(n))无解.

证明：混合函数方程

Z(n)=S2(sim(n))

(1)

的解主要分以下两种情形讨论：

情形一：当n≡0(mod9)时，有S2(sim(n))=S2(9)=min{m:29|m!}=12(由引理1-引理3可得)，即Z(n)=12.

现令n=9l(l=1，2，…),由引理4-引理6知，不存在这样的n可使得Z(n)=12,故此时(1)式无解.

情形二：当n≡r(mod9)时，有S2(sim(n))=S2(r)=min{m:2r|m!}(其中0

当r=1,S2(1)=2,即Z(n)=2,此时n=3,代入(1)式验证不符合，故此时(1)式无解.

当r=2,S2(2)=4,即Z(n)=4,此时n=5，10,分别代入(1)式验证均不符合，故此时(1)式无解.

当r=3,S2(3)=4,即Z(n)=4,此时n=5，10,分别代入(1)式验证均不符合，故此时(1)式无解.

当r=4,S2(4)=6,即Z(n)=6,此时n=7，21,分别代入(1)式验证均不符合，故此时(1)式无解.

当r=5,S2(5)=8,即Z(n)=8,此时n=9，12，18，36,分别代入(1)式验证均不符合，故此时(1)式无解.

当r=6,S2(6)=8,即Z(n)=8,此时n=9，12，18，36,分别代入(1)式验证均不符合，故此时(1)式无解.

当r=7,S2(7)=8,即Z(n)=8,此时n=9，12，18，36,分别代入(1)式验证均不符合，故此时(1)式无解.

当r=8,S2(8)=10,即Z(n)=10,此时n=11，55,分别代入(1)式验证均不符合，故此时(1)式无解.

定理2：对于任意的正整数n,混合函数方程Z(n)=S3(sim(n))的解为n=24，60.

证明：混合函数方程

Z(n)=S3(sim(n))

(2)

的解主要分以下两种情形讨论：

情形一：当n≡0(mod9)时，有S3(sim(n))=S3(9)=min{m:39|m!}=21(由引理1-引理3可得)，即Z(n)=21.

现令n=9l(l=1，2，…),由引理4-引理6知，不存在这样的n可使得Z(n)=21,故此时(2)式无解.

情形二：当n≡r(mod9)时，有S3(sim(n))=S3(r)=min{m:3r|m!}(其中0

当r=1,S3(1)=3,即Z(n)=3,此时n=2，6,分别代入(2)式验证均不符合，故此时(2)式无解.

当r=2,S3(2)=6,即Z(n)=6,此时n=7，21,分别代入(2)式验证均不符合，故此时(2)式无解.

当r=3,S3(3)=9,即Z(n)=9,此时n=45,sim(45)=9与前提条件矛盾，故此时(2)式无解.

当r=4,S3(4)=9,即Z(n)=9,此时n=45,sim(45)=9与前提条件矛盾，故此时(2)式无解.

当r=5,S3(5)=12,即Z(n)=12,此时n=13，26，39，78,分别代入(2)式验证均不符合，故此时(2)式无解.

当r=6,S3(6)=15,即Z(n)=15,此时n=24，40，60，120,分别代入(2)式验证，此时(2)式有解为n=24，60.

当r=7,S3(7)=18,即Z(n)=18,此时n=19，57，171,分别代入(2)式验证均不符合，故此时(2)式无解.

当r=8,S3(8)=18,即Z(n)=18,此时n=19，57，171,分别代入(2)式验证均不符合，故此时(2)式无解.

定理3：对于任意的正整数n,混合函数方程Z(n)=S5(sim(n))的解为n=11，120.

证明：混合函数方程

Z(n)=S5(sim(n))

(3)

的解主要分以下两种情形讨论：

情形一：当n≡0(mod9)时，有S5(sim(n))=S5(9)=min{m:59|m!}=40(由引理1-引理3可得)，即Z(n)=40.

现令n=9l(l=1，2，…),由引理4-引理6知，不存在这样的n可使得Z(n)=40,故此时(3)式无解.

情形二：当n≡r(mod9)时，有S5(sim(n))=S5(r)=min{m:5r|m!}(其中0

当r=1,S5(1)=5,即Z(n)=5,此时n=15,代入(3)式验证不符合，故此时(3)式无解.

当r=2,S5(2)=10,即Z(n)=10,此时n=11，55,分别代入(3)式验证，此时(3)式有解n=11.当r=3,S5(3)=15,即Z(n)=15,此时n=24，40，60，120,分别代入(3)式验证，此时(3)式有解n=120.

当r=4,S5(4)=20,即Z(n)=20,此时n=42，70，210,分别代入(3)式验证均不符合，故此时(3)式无解.

当r=5,S5(5)=25,即Z(n)=25,此时n=65，325,分别代入(3)式验证均不符合，故此时(3)式无解.

当r=6,S5(6)=25,即Z(n)=25,此时n=65，325,分别代入(3)式验证均不符合，故此时(3)式无解.

当r=7,S5(7)=30,即Z(n)=30,此时n=31，93，155，465,分别代入(3)式验证均不符合，故此时(3)式无解.

当r=8,S5(8)=35,即Z(n)=35,此时n=63，90，315，630,而sim(63)=9、sim(90)=9、sim(315)=9、sim(630)=9,均与前提条件矛盾，故此时(3)式无解.

3 相关推论

证明：用数学归纳法易得.