船舶参数横摇非线性力学特征数值分析

杨 波，王 骁，吴 明

（海军大连舰艇学院 航海系，辽宁 大连116018）

0 引 言

当船舶纵浪航行时，复原力矩会随船体与波浪相对位置的改变而发生变化，对于具有较大外飘船首和方尾的船型，这种变化尤为明显。此时很小的初始横向扰动也有可能导致大幅横摇运动，这种现象称为参数横摇。一般认为，当海浪波长与船长近似相等、船舶与海浪的遭遇频率约为横摇固有频率的2倍时，最易发生参数横摇。目前国际海事组织（IMO）正在推进的“第二代完整稳性衡准”中，将参数横摇作为船舶波浪中5种稳性失效模式之一，是目前船舶水动力学领域研究的热点。

参数横摇的研究方法主要有模型试验和理论研究两种。理论研究方面，Pauling和Rosenberg（1959）[1]最早采用单自由度马休方程对参数横摇进行求解，并假定波浪中初稳性高按弦值函数变化，但该方法对参数横摇的预报并不准确。随着研究不断深入，研究者开始注意到横摇阻尼、非线性复原力矩和其它自由度运动对参数横摇的影响，并开展了相关研究。对于横摇阻尼，常用方法是基于横摇衰减实验数据，将其表示为横摇角速度的高阶函数[2-3]。对于非线性复原力矩，则采用横摇角的高阶多项式表达，然后对与波浪相关的时变项进行修正[4-5]。除此之外，许多学者还利用基于势流理论的切片法[6-7]和三维面元法[8-9]计算时变复原力矩。Spanos等（2009）[10]对14种时域势流方法进行了比较研究，结果表明三维面元法较切片法能更好地模拟参数横摇，但所有方法对大幅运动的波浪水动力计算均较差。对于其他自由度的影响，Bulian（2005）[11]提出了一种1.5自由度模型，以研究垂荡和纵摇对参数横摇的影响；更多的学者通过横摇-纵摇-垂荡三自由度模型[12-13]以及近年来发展起来的操纵/耐波六自由度统一模型[18-20]，对参数横摇运动进行研究。鲁江等[14-15]对随机波浪中的参数横摇进行了研究，验证了随机波浪下参数横摇的非各态历经特点。

可以看出，理论研究中，对于参数横摇影响较大的复原力矩和非线性阻尼，均采用近似方法进行计算，尽管做了若干修正，但在船舶大幅横摇时仍然存在误差。模型实验是研究参数横摇的可靠方法，但较为费时费力，且不易开展单项影响因素的深入研究。目前，计算流体力学方法（CFD）已广泛运用于船舶水动力计算，其基于粘性流理论，相较于势流理论有着天然优势，可精确计算船舶在波浪环境中的水动力和力矩，这为基于力学方法研究参数横摇提供了可能。Hamid等（2010）[23]采用CFD方法模拟了一艘水面舰艇的迎浪参数横摇运动，与水池实验结果吻合较好，但是国内基于CFD方法的参数横摇研究相对较少。

复原力矩和横摇阻尼是影响参数横摇模拟的重要因素。作者曾基于CFD方法对船模的静水横摇衰减运动进行数值模拟研究[24]，数值模拟结果与水池实验吻合良好，验证了CFD方法用于数值计算横摇复原力矩和阻尼的有效性。本文在前述研究的基础上，基于CFD方法研究了DTMB5512船模顶浪航行时的参数横摇运动。实验涵盖多种航速和波高，分析了波浪遭遇周期和波高对参数横摇的影响。基于实验结果，对激励船模发生参数横摇时复原力矩的非线性特征进行了分析，并对产生非线性特征的原因进行了探讨。本文方法可对瘦削船型顶浪航行时的参数横摇进行预报，为参数横摇的力学特征分析提供了新的方法，可用于船模的波浪中完整稳性的定量评估。

1 CFD数学模型

1.1 流体控制方程

船舶水动力研究可将水视为不可压缩粘性流体，控制方程包括连续性方程和动量方程（N-S方程），其张量表示为：

式中：ui、uj分别为流体速度矢量⇀u在xi、xj方向的分量，t为时间，P为压力，ρ为流体密度，fi为质量力，μ为流体动力粘性系数。

采用RNGk-ε模型模拟湍流，使上述方程组封闭，湍动能k及湍流耗散率ε的控制方程的张量表示为：

1.2 波浪数学模型

采用船舶耐波性水池实验中常用的微幅波模型模拟波浪。假设船舶静止，建立以船舶重心为原点，X轴正向指向船尾，Y轴正向指向船舶右舷，Z轴正向垂直向上的船体坐标系，基于相对运动原理，可得波浪波高方程为：

速度方程为：

式中：u、v、w分别为x、y、z三个方向的速度，H为波高，k为波数，ω 为波浪圆频率，V为航速，ε0为初始相位。

2 数值模拟方案

2.1 船模选择

选择国际拖曳水池会议（International Towing Tank Conference，ITTC）推荐船型DTMB5512船模为研究对象，其型线图如图1所示，主要船型参数如表1所示。从型线图中可以看出，该船型具有外飘船首和方形尾，是易发生参数横摇的船型。

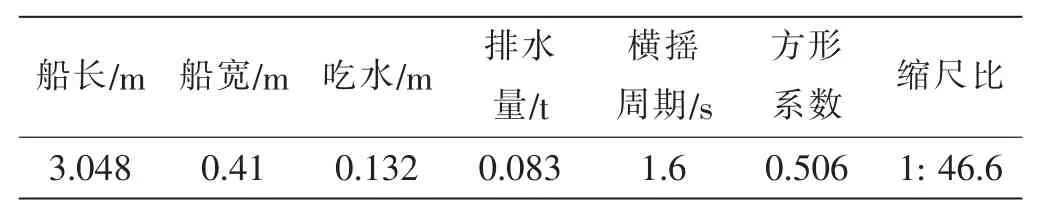
表1船模主要参数Tab.1 Parameters of ship model

2.2 实验参数

参数横摇影响因素较多，遭遇周期（Te）和波高（H）是比较重要的两项，且当波长（λ）一定时，遭遇周期只受航速（V）影响。选择最易发生参数横摇的波长（λ=L，L为船长，下同），波高/波长比（H/λ）为 0.04，进行多种付汝德数（Fr）下数值模拟，具体实验参数如表2所示。

图1船模型线图Fig.1 Ship model’s body plan

表2实验参数Tab.2 Parameters of simulation

2.3 计算域划分及网格生成

（1）计算域划分

计算域为长方体，长、宽、深为 4L×2L×1.7L（L为船长），其中入口距船首1L，船尾距消波区1L，另有长1L的消波区，水深1L，自由面距上边界0.7L，船模与水池相对位置如图2所示。

（2） 网格生成

采用混合网格，在船体周围区域采用非结构网格以较好地表现船型，其余区域采用结构网格以减少网格数量并提高计算效率，在自由面附近进行网格加密以满足造波要求。船体面网格尺寸为0.01 m，布置5层边界层网格，第一层网格厚度保证y+<30，总网格数为255万。舰首部分面网格及球鼻首附近边界层网格如图3所示。

图2计算域Fig.2 Computational domain

图3船首面网格及边界层网格Fig.3 Mesh of ship bow and boundary layers

2.4 边界条件设置

采用边界造波法模拟波浪，计算域的边界条件具体设置如下：

入口边界—速度入口，按照（3）-（4）式给定波高及速度值；

出口边界—压力出口，设置静水压力；

船体—壁面，有剪切力无滑移；

外边界（包含水池底部、顶部及侧壁）—壁面，剪切力为0。

2.5 其他设置

采用VOF方法追踪自由面，采用壁面函数法模拟近壁面流动，VOF方程离散采用改进的HRIC格式，其余方程采用二阶迎风格式，速度压力耦合方程求解采用SIMPLEC算法。每个时间步内迭代求解20次，当主要物理量残差小于10-4时，该时间步计算收敛，进行下一时间步计算。

数值模拟时，将船模以初始横倾角3°置于顶浪流场中，以提供初始横摇扰动；待流场稳定后，使船模做横摇/纵摇/垂荡三自由度耦合运动。

3 数值模拟结果及分析

3.1 数值模拟结果

图4是未发生和发生参数横摇时典型的横摇角变化时历，图中t为时间，φ为横摇角。

可以看出，由于初始横倾角的存在，舰船会在复原力矩作用下发生横摇运动，当不发生参数横摇时，横摇角幅值逐渐变小为0；当发生参数横摇时，横摇角幅值则会不断增大，直至达到最大值并保持稳定。

通过横摇时历曲线可得稳定横摇角幅值（φ0），不同航速下的φ0如表3所示。

从表中可以看出：

（1）航速对是否发生参数横摇有重要影响。对于该型船来说，发生参数横摇的航速主要集中于中高速段；

（2）发生参数横摇的四个速度对应的波浪遭遇周期分别为0.859、0.797、0.744和0.698 s（见表2）。可见，当航速使遭遇周期Te接近Tφ/2（Tφ为横摇周期，见表1）时，易发生参数横摇；且愈接近，最大横摇角幅值愈大。这与已有研究成果相符。

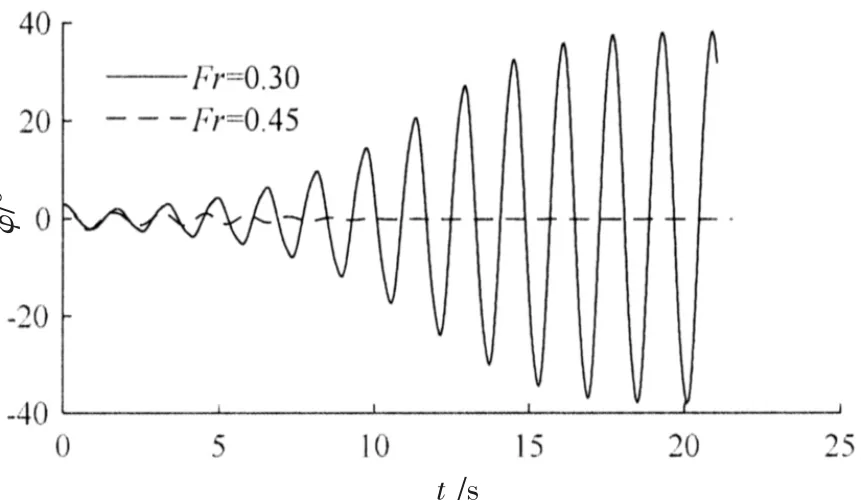
图4未发生/发生参数横摇时的横摇时历曲线Fig.4 Time history of non-/parametric rolling

表3不同航速时的稳定横摇幅值Tab.3 Steady rolling amplitudes at different speeds

图5是发生参数横摇时不同航速下横摇时历曲线，图中t为时间，φ为横摇角。

从图中可以看出：

（1）当Fr=0.25、0.30、0.35和0.40时，达到稳定横摇状态分别用了22、12、15和27个横摇周期，可见当遭遇周期越接近Tφ/2时，达到稳定横摇所需时间越少。

（2） 经计算，稳定横摇时，Fr=0.25、0.30、0.35 和 0.40 对应的横摇周期分别为 1.728 s、1.596 s、1.486 s和1.400 s，基本为遭遇周期的2倍。

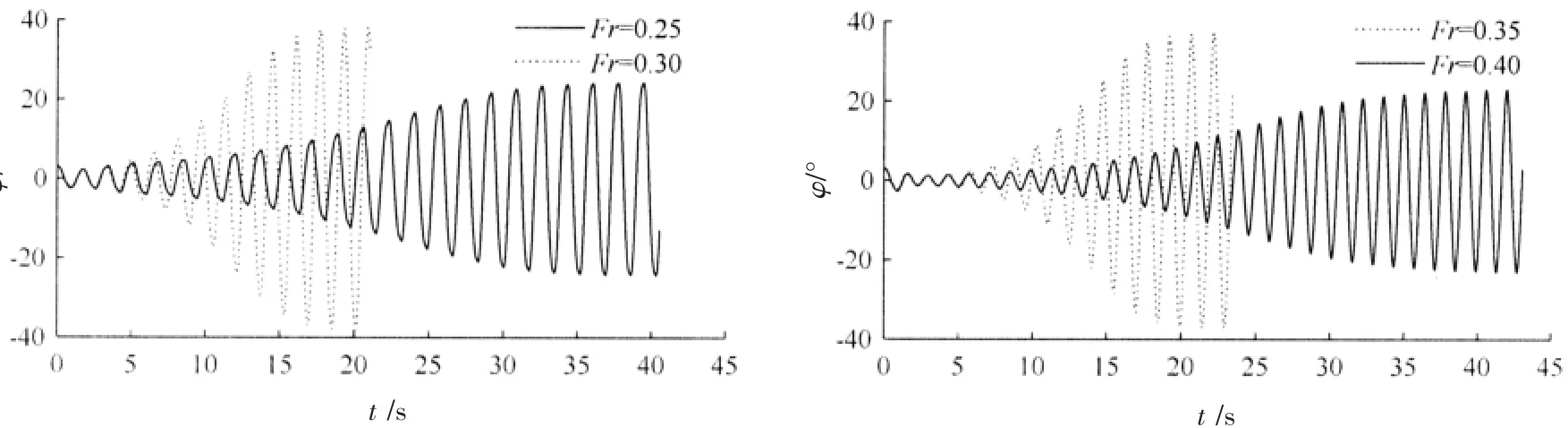
图5不同航速参数横摇时历曲线Fig.5 Time history of parametric rolling at different speeds

3.2 参数横摇非线性力学特征分析

导致参数横摇发生的直接原因在于横摇力矩的非线性变化。图6为发生参数横摇时横摇复原力矩变化时历，图中t为时间，Mφ为横摇复原力矩。其中6（a）为初始至稳定横摇整个过程，而6（b）为一个横摇周期内的复原力矩与横摇角变化对比图。

从图中可以看出：

（1）复原力矩幅值从由小变大，直至稳定横摇时保持不变；

（2）复原力矩曲线会随横摇角增大而出现2个拐点，呈现出先增大、后减小、再急剧增大的非线性特征。尤其是在参数横摇发展初始阶段，这一减小过程尤为明显，复原力矩值会接近于0，甚至会降为负值（力矩方向发生改变）。正是这一过程，使得舰船不能及时扶正，而在惯性作用下横摇不断增大；而减小过程结束后，复原力矩又迅速增大，使舰船在2/4周期中加速回摇，以较大的角速度通过正浮位置，摇向另一舷。在后1/2周期中，又出现与前1/2周期相同的过程（区别在于力矩方向改变）。如此反复，促使横摇角越来越大，产生参数横摇。

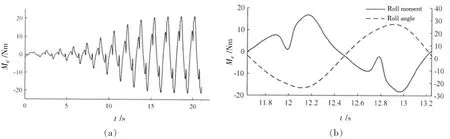
图6复原力矩时历曲线Fig.6 Time history of restoring moment

3.3 横摇力矩非线性特征原因分析

基于数值模拟结果，本文发现，参数横摇复原力矩曲线的非线性与纵摇、垂荡及船/波相对位置曲线呈现强相关性，其特征点（零点、2个拐点及最大值点）可以分别用垂荡、纵摇和船/波相对位置表征。图7为一个横摇周期内复原力矩、纵摇和垂荡时历对比图，图中t为时间，Mφ、θ、Z为复原力矩、纵摇和垂荡值（为便于比较，图中Z值乘以100）。图8为船模周围瞬时波高图，图8（a）、（b）、（c）、（d）分别对应图 7 中 A、B、C、D 点，可见B、C为拐点，D为复原力矩最大点。

从图中可以看出：

（1）A时刻船模横摇角为0，复原力矩接近于0，此时波峰距船首约1/4船长，船模位置上浮，船体稍尾倾。

（2）A至B时刻，波谷逐渐向船首移动，导致水面降低，同时船模向上运动，并处于尾倾状态，导致船首部排水体积迅速减小。但由于横摇角增大，复原力矩仍然增大。B点对应垂荡最高点，此时船首排水体积达到最小值，复原力矩开始变小。

（3）B至C时刻，船模开始下沉，并由尾倾过渡到首倾，但由于波谷通过船体前部，波面继续降低，导致船模前部排水体积继续减小。此时虽然横摇角在惯性作用下继续增大，但复原力矩不断减小。C点时波谷距舰首距离约1/4船长，此时复原力矩降至最小。

图7复原力矩、纵摇和垂荡时历曲线Fig.7 Time history of restoring moment,pitch and heave

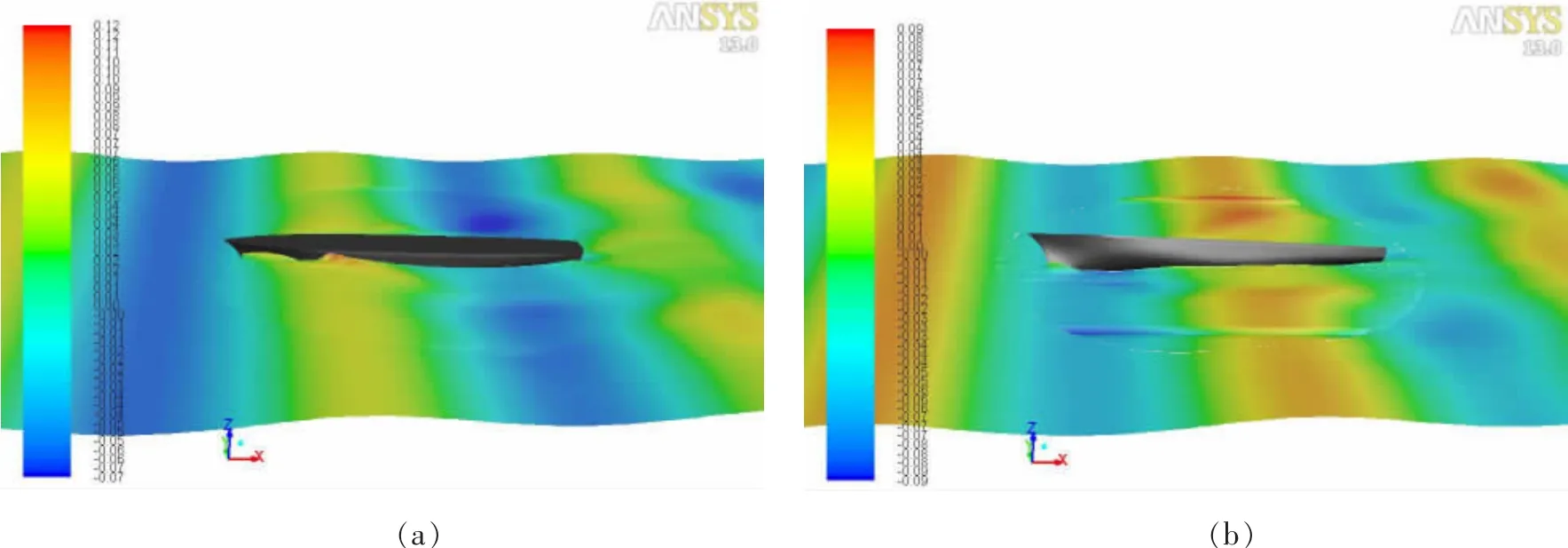
图8不同时刻瞬时波高图Fig.8 Transient wave height at different times

（4）C至D时刻，船模继续下沉，船体首倾继续增大，同时波峰向船首移动，水面上升，导致船首部排水体积迅速增加，同时横摇角继续增大，使得复原力矩迅速增大。D点对应首倾最大值点，复原力矩达到最大值。

（5）D时刻后，船模在复原力矩作用下回摇，横摇角迅速归零，向另一舷运动。同时，从图7中可以看出，纵摇及垂荡周期等于波浪遭遇周期，而横摇周期为2倍遭遇周期。这使得纵摇、垂荡及船/波相对运动影响周期性作用于横摇复原力矩，从而产生参数横摇。

4 结 论

本文基于CFD方法，对某瘦长型船模在规则波中顶浪航行时的参数横摇运动进行了数值模拟。模拟结果表明，当航速使波浪遭遇周期约接近于Tφ/2时，越容易发生参数横摇，横摇值也越大。这与现有研究成果是相符的，证明了CFD方法用于参数横摇模拟的有效性。通过对参数横摇时复原力矩的非线性特征和产生原因进行分析，可得到以下结论：

（1）船体排水体积的变化是复原力矩变化的直接原因。对于具有较大外飘角的船型，船首部的排水体积变化对复原力矩变化起主要作用，而这一变化受纵摇、垂荡和船/波相对位置共同作用。

（2）参数横摇力矩曲线在横摇角变大过程中会出现2个拐点，呈现出先增大、后减小、再增大的非线性特征。当波长等于船长时，曲线的4个特征点（零点、2个拐点和最大值点）可以分别由波峰距船首1/4船长、垂荡最大值点、波谷距船首1/4船长、首倾最大值点进行表征。

（3）顶浪运动使船舶纵摇和垂荡周期等于波浪遭遇周期，而使横摇周期基本为2倍遭遇周期。这使得纵摇、垂荡及船/波相对位置周期性地对复原力矩产生影响，从而导致参数横摇。

（4）基于CFD方法可以对参数横摇时的非线性复原力矩进行准确计算和分析，这是以往方法所难以实现的。

本文研究仅对波长等于船长及顶浪运动工况进行了数值模拟，下一步将开展不同波长及不同航向工况的参数横摇研究。