船舶艉轴承刚度和螺旋桨陀螺效应对轴系回旋振动特性影响的分析

李小军，朱汉华，范世东，郑良焱

（武汉理工大学 能源与动力工程学院，武汉 430063）

0 引 言

船舶轴系上旋转质量的不平衡离心力，以及来自不均匀伴流场、作用在螺旋桨上的流体激振力将使轴系产生回旋振动。回旋振动严重时将导致轴系运行不稳定，甚至影响船舶航行安全[1]。

一般滑动轴承的水平方向的刚度相对于垂直方向要低一些。随着船舶的大型化，船体尾部刚度逐渐下降，而螺旋桨质量和转动惯量却比较大。后艉轴承的位置比较特殊，起着支撑艉轴和螺旋桨的作用，其承受着来自螺旋桨剧烈的动载荷作用，工作条件恶劣，润滑状态不稳定，载荷呈边缘效应，甚至导致干摩擦，这些都会引起总支承刚度的变化[2]。因此对于大型低速船舶，为了保证轴系运转正常和船舶航行安全，进行尾轴承刚度各向异性下的轴系回旋振动研究是有必要的。

目前对于轴系回旋振动的研究，由于资料的缺乏，以及轴承刚度的难测性，大多是建立在刚性轴承、或者轴承刚度各向同性的基础之上的，而未将轴与轴承作为“柔性轴-柔性支撑”来进行研究；还有学者将其退化为横向振动进行研究，而忽略了螺旋桨在转子结构中产生的陀螺效应[3]。

陈之炎等[4]对回旋振动的机理进行了详细的研究，并从理论上讨论了支承刚度各向异性的情况。王磊等[5]借助有限元软件，分析了螺旋桨陀螺效应、应力刚化效应和旋转软化效应等对回旋振动的影响。

本文以某TEU集装箱船的推进轴系为研究对象，借助于有限元软件ANSYS，计入螺旋桨的陀螺效应，分析船舶推进轴系后艉轴承各向异性时回旋振动的特性，包括其固有频率、坎贝尔图临界转速和回旋振动响应。

1 考虑陀螺效应的轴系振动方程

根据弹性力学，对于轴系这样的多自由度弹性系统，其通用动力学运动方程为：

式中：［M］、 ［C］和 ［K］分别代表质量矩阵、阻尼矩阵和刚度矩阵；｛u¨｝、 ｛u˙｝和 ｛u｝分别代表加速度向量、速度向量和位移向量；｛F｝代表广义外力。

由于船舶螺旋桨的质量和惯量都比较大，会对轴系回旋振动产生较大影响，因此在轴系回旋振动的计算中需要考虑螺旋桨的陀螺效应。

当轴承各向同性时，螺旋桨的陀螺力矩：

式中：Jp为极转动惯量，Jd为径向转动惯量，j0为转动惯量比为频率比可知，陀螺力矩包含2项为哥氏惯性力矩为牵连惯性力矩。陀螺力矩为正值时，其方向与转轴旋转方向相反，减少了轴系的弯曲变形量，相当于轴的弯曲刚度变大了，轴系的固有频率因此增加；反之，则使轴系的固有频率下降。

当轴承支承刚度各向异性时，其陀螺力矩为：

式中：x方向为轴线方向为z方向的转角速度为z方向的转角加速度；同理为y方向的转角速度为y方向的转角加速度。

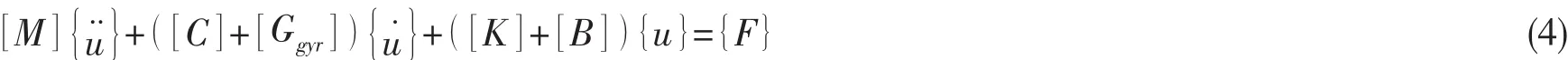
式中：［Ggyr］为陀螺效应矩阵，主要取决于自转角速度ω，与公转角速度Ω无关[6]。［］B为旋转阻尼矩阵，在低转速下影响较小，在本文中不计入。

在有限元软件ANSYS的固定坐标系中，计入螺旋桨陀螺效应后的转子的动力方程为：

2 分析模型

2.1 轴系主要参数

本文采用的研究对象是某TEU船推进轴系，轴系从主机至螺旋桨全长47.763 m，中间轴轴径为795 mm，艉轴外径975 mm，内径330 mm，含三个中间轴承和一个前艉轴承、一个后艉轴承。螺旋桨为6叶定距桨，根据Jasper给出的计算公式，螺旋桨附连水的质量、极转动惯量和径向转动惯量系数分别取1.1、1.25和1.5，得螺旋桨附水质量为120 353 kg，附水极转动惯量为454 250 kg·m2，附水径向转动惯量为 272 550 kg·m2。

2.2 模型建立与简化

（1）建模时为了尽可能模拟船舶推进轴系的状态，同时考虑螺旋桨的陀螺效应，选用beam188单元对轴段进行模拟，对于轴段上的联轴器，通过设置梁的截面来模拟。

（2）螺旋桨的桨毂部分，通过适当延长尾轴长度来模拟。螺旋桨及附连水的质量和转动惯量较大，采用mass21质量单元，施加在螺旋桨的几何中心位置。

（3）对于径向轴承，采用combine14弹簧单元进行模拟，在每个支撑位置的垂直和水平方向分别设置一个弹簧单元。弹簧的一端与轴系上的轴承对应节点相连，另一端设置为固定端。

（4）由于进行回旋振动分析，因此对弹簧单元的固定端施加全约束，对主机端的节点约束其全部自由度，约束轴系在UZ和ROTZ上的自由度[7]。

简化后的轴系模型如图1和图2所示。

图1 轴系有限元模型（显示单元） Fig.1 Finite element model of shafting (unit displayed)

图2 轴系有限元模型（显示约束）Fig.2 Finite element model of shafting(constraints displayed)

3 计算结果分析与讨论

径向轴承的支承刚度是轴系回旋振动的重要影响之一，它是由若干因素决定的，例如轴承结构、轴承材料、轴承间隙、油膜等，所以精确测量支承刚度是很困难的。

在船舶轴系实际运转中，滑动轴承垂直方向上的刚度要比水平方向上的刚度值大，轴的中心环绕着的旋转中心的轨迹是一个椭圆而不是一个圆形，因此在回旋振动时可能出现水平和垂直方向上两个临界转速[7]。但是其差距并不大，为研究后尾轴承水平方向刚度值单独变化对回旋振动影响，在本文中将两个方向上的刚度差距放大至一个数量级，以便观察其对轴系振动影响的变化规律。

由于篇幅有限，在本文以下的研究中，用刚度符号①代指后艉轴承刚度特性为水平刚度4.6×108/N·m-1，垂直刚度 4.6×108/N·m-1，用刚度符号②代指后艉轴承刚度为水平刚度 4.6×108/N·m-1，垂直刚度4.6×109/N·m-1，用刚度符号③代指后艉轴承刚度为水平刚度 4.6×109/N·m-1，垂直刚度 4.6×109/N·m-1。其他轴承各方向上的刚度为定值，均保持水平刚度4.6×109/N·m-1，垂直刚度4.6×109/N·m-1。

3.1 固有频率计算

由于引入了螺旋桨的陀螺效应，采用QR阻尼法，所得的特征值为复数，其虚部为进动（回旋）频率，实部为衰减系数，且特征值成对出现，对应正回旋和逆回旋的固有频率。按照上面的代指规则，依次改变后艉轴承刚度，分别在计入陀螺效应和不计入陀螺效应这两种情况下进行模态分析，得到其前三阶正逆回旋固有频率，如表1和表2所示。

表1不计陀螺效应时正逆回旋固有频率Tab.1 Natural frequency of forward and inverse whirling vibration without considering the gyroscopic effect

表2计入陀螺效应时正逆回旋固有频率Tab.2 Natural frequency of forward and inverse whirling vibration considering the gyroscopic effect

得到不同刚度下各阶回旋振动在计入（不计入）螺旋桨陀螺效应时的相对变化量，如表3所示。

对数据进行处理，采用以下公式：

表3相对变化量Tab.3 The relative change amount

由表1-3可知，不计入陀螺效应时，回旋振动便退化为横向振动。当后尾轴承垂直方向的刚度与水平方向刚度相同时，轴系会出现两个成对（共轭方向）的回旋振动固有频率，其值大小相同；当后尾轴承垂直方向的刚度与水平方向刚度不相同时，例如保持垂直方向刚度不变，当水平方向的刚度单独降低，则水平方向上对应的回旋振动固有频率降低，即相应临界转速降低，而垂直方向上的回旋振动固有频率不变化。这说明，不计陀螺效应时，轴承某一方向上的刚度变化只会影响到该方向上横向振动固有频率（临界转速），而不会影响其他方向。

计入螺旋桨陀螺效应时，相较于不计入螺旋桨陀螺效应（横向振动）而言，当水平方向刚度降低时，逆回旋固有频率会在水平横向振动固有频率的基础上进一步降低；正回旋各阶固有频率会略微提高，但是其相对变化量与逆回旋各阶固有频率的相对变化量大小相近。这说明螺旋桨的陀螺力矩在正回旋（正进动）时提高了临界转速，在逆回旋（反进动）时降低了临界转速，且其对正逆回旋的影响相当。

比较上面后艉轴承刚度各向同性与各向异性两种情况，发现当后艉轴承刚度各向异性时，计入陀螺效应与不计入陀螺效应的相对变化量很小，即此时螺旋桨的陀螺效应远远没有各向同性时显著。再分析公式（2）和公式（3），推断这可能是由以下两个因素造成的：

（1）根据公式（2），支承各向同性时陀螺效应包含科氏力矩（由自转角速度决定）和惯性力矩JdΩωθ（由公转角速度和自转角速度决定）。ANSYS中陀螺效应是建立在高速轴的基础上，即假定转子自转角速度远远大于公转角速度，因此其陀螺力矩主要是由转子自转角速度决定的。而本文中研究对象为大型低速集装箱船，其轴系转速较低，而公转角速度有可能与自转角速度处于同一数量级，甚至更大，因此其牵连惯性力矩在陀螺效应中所作贡献不可以忽略。根据可以判断ANSYS在轴承各向同性时所计算的陀螺效应要比实际的陀螺效应大。

（2）根据公式（3），当轴承刚度各向异性时，其相互垂直两个方向的陀螺力矩主要取决于轴系自转角速度 ω、转角速度和转角加速度而本文中轴系自转角速度很低，因此陀螺效应影响不大。

3.2 坎贝尔图计算

通常在船舶轴系回旋振动计算中，由于伴流场的激励特性，一般只需要求出轴频、叶频和倍叶频的正逆回旋振动临界转速就可以了[8]。改变轴系的自转角速度，分别画出刚度①、刚度②和刚度③的坎贝尔图，如图3-5所示。

图3刚度①的坎贝尔图 Fig.3 Campbell diagram of stiffness①

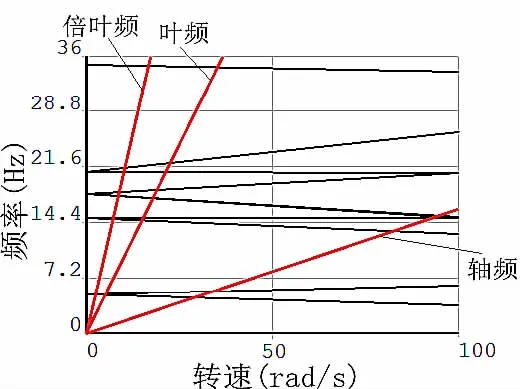
图4刚度②的坎贝尔图Fig.4 Campbell diagram of stiffness②

由图3-5可知，随着转速的提高，在陀螺效应的作用下，轴系各阶正回旋临界转速逐渐提高，逆回旋临界转速逐渐降低，这与理论相符。

当后艉轴承刚度由水平刚度4.6×109/N·m-1，垂直刚度4.6×109/N·m-1变化为水平刚度 4.6×108/N·m-1，垂直刚度 4.6×108/N·m-1时，其正逆回旋各阶临界转速均降低，但是此时其正逆回旋线仍在零转速（横向振动）处重合；当后艉轴承刚度由水平刚度4.6×109/N·m-1，垂直刚度 4.6×109/N·m-1变化为水平刚度 4.6×108/N·m-1，垂直刚度 4.6×109/N·m-1（即水平方向刚度单独变化），其逆回旋线降低，而正回旋线变化不大，此时其正逆回旋临界转速线在零转速（横向振动）处不重合。

图5刚度③的坎贝尔图Fig.5 Campbell diagram of stiffness③

3.3 临界转速计算

由于该船轴系的额定转速为104 r/min，即10.888 5 rad/s，在轴系启动到额定转速这段范围内，有可能出现叶频和倍叶频的临界转速，通过坎贝尔图计算得到其前三阶正逆回旋的轴频、叶频和倍叶频的临界转速，如表4所示。

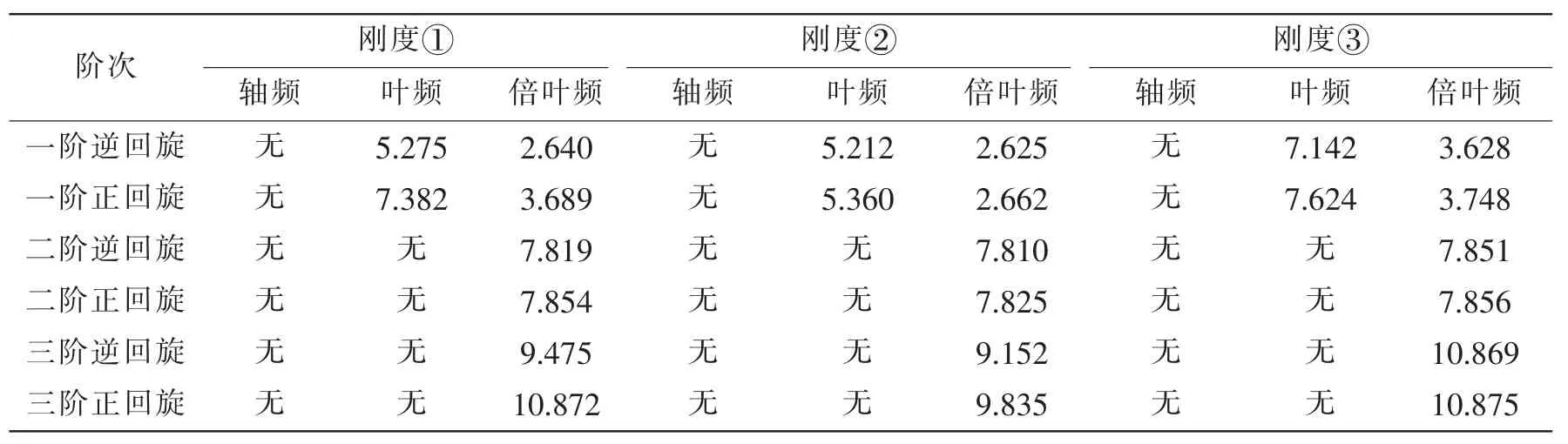
表4 前三阶正逆回旋临界转速（rad/s）Tab.4 Critical speed of first three forward and inverse whirling vibration(rad/s)

由表4可知，上面三种刚度下，在该船额定转速范围内，均不会经过轴频所对应的临界转速，但是会经过叶频和倍叶频所对应的临界转速。不管是叶频还是倍叶频，当轴承水平方向上的刚度单独从K1降低到K2时，逆回旋的临界转速也随之降低，介于K1和K2对应的临界转速ω1和ω2之间，接近ω2；正回旋的临界转速略微降低，也是介于K1和K2对应的临界转速ω1和ω2之间，接近ω1。

3.4 振动响应评估

螺旋桨在船尾不均匀伴流场中运转时，螺旋桨受水动力以叶频为基频的激振力和激振力矩作用，通过轴承传递给船体，这是轴系振动的主要原因。在该节中，采用的正弦激振力为8.45 kN，横向施加在螺旋桨对应的节点上。

通过上一节的分析发现，这三种刚度下的轴系一阶固有频率均在10 Hz以下，选定强迫振动的频率范围为0~10 Hz，仍然选取与上节相同的三种刚度，进行谐响应分析。选取螺旋桨、后尾轴承、前尾轴承这几个具有代表性的位置，分析其受力方向的最大振动响应位移，其结果如表5所示，幅频曲线如图6-8所示。

表5轴系各关键位置最大位移（mm）Tab.5 Maximum displacement of the key positions(mm)

从表5和图6-8可以看出，在一定轴承刚度下，轴系的振动响应位移大致从螺旋桨至推力轴承呈递减趋势，即螺旋桨处振动位移响应最大。一般情况下，轴承某方向上的刚度越大，则该方向的振动响应位移越小。

轴承刚度各向异性时，例如当轴承水平方向上的刚度从K1降低到K2时，在水平方向的激励下，该方向上的最大响应位移ζ也随之增大；而在其相互垂直的方向上产生的位移相对来说较小，可忽略不计。当在垂直方向施加同样的激励时，垂直方向上最大位移响应略小于K1对应的最大位移响应ζ1，这需要进一步探讨。

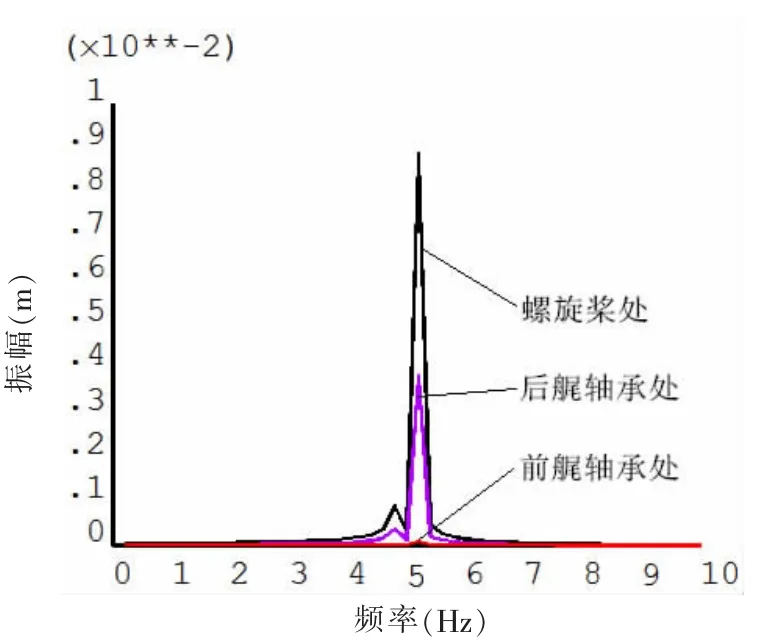
图6刚度①的幅频曲线Fig.6 The Amplitude-Frequency curve of stiffness①

图7刚度②的幅频曲线Fig.7 The Amplitude-Frequency curve of stiffness②

图8刚度③的幅频曲线Fig.8 The Amplitude-Frequency curve of stiffness③

4 结 论

本文以转子动力学为基础，分析了公式法与ANSYS有限元法在计算陀螺效应时的异同，建立了某船舶推进轴系的有限元模型，并在后艉轴承刚度各向同性和各向异性的情况下，分析了其在额定转速下的回旋振动固有频率，得到轴频、叶频和倍叶频的临界转速，以及对振动响应做出了分析与评估。其结论如下：

（1）不计陀螺效应时，轴承某一方向上的刚度变化只会影响到该方向上横向振动固有频率（临界转速），而不会影响其他方向。计入陀螺效应时，螺旋桨的陀螺力矩在正回旋（正进动）时提高了临界转速，在逆回旋（反进动）时降低了临界转速，且其对正逆回旋的影响相当。有限元软件ANSYS在后艉轴承各向同性时计算陀螺效应与实际有一定偏差。

（2）随着转速的提高，在陀螺效应的作用下，轴系各阶正回旋临界转速逐渐提高，逆回旋临界转速逐渐降低。在坎贝尔图中，后艉轴承刚度各向同性时，其正逆回旋曲线在零转速（横向振动）处重合；后艉轴承刚度各向异性时，其正逆回旋曲线在零转速（横向振动）处不重合。

（3）在一定轴承刚度下，轴系的振动响应位移大致从螺旋桨至推力轴承呈递减趋势。一般情况下，轴承某方向上的刚度越大，则该方向的振动响应位移越小。