柔性基础准零刚度隔振系统吸引子迁移控制研究

2019-07-30赵建学朱石坚

船舶力学 2019年7期

俞翔，赵建学，柴凯，朱石坚

（海军工程大学 a.舰船与海洋学院；b.动力工程学院，武汉 430033）

0 引言

准零刚度隔振系统高静低动的刚度特性不仅能实现系统的低频隔振，还有较大的承载能力[1-2]，特别适用于舰船动力设备的隔振，受到了国内外学者的广泛关注。然而，准零刚度隔振系统是非线性系统，相同参数条件但不同初始条件下有可能对应多种运动状态，即存在吸引子共存现象。系统运行在不同吸引子上时具有不同的隔振效果，为保证系统处于最优的隔振状态，可实施吸引子的迁移控制，即通过控制使得当系统运行于大振幅吸引子上时迅速迁移至振幅较小的吸引子上，从而降低基座振动，实现减振降噪。因此，研究吸引子的迁移控制具有重要的理论和实际意义。

Jackon等最早提出了开环控制方法[3]、参数开环控制方法[4]来控制混沌，但存在无法确定系统的吸引域和收敛域的缺点[5-6]。开环加闭环控制方法[7]和参数开环加闭环控制[9]弥补了这些不足，并且已成功应用于很多复杂的非线性系统。如陈立群等应用开环加闭环控制方法研究了离散动力系统混沌、超混沌的控制问题[8]，并以控制Lorenz混沌为例说明了参数开闭环控制方法的应用[9]。戈新生等[10]将开环加闭环控制方法应用于3D刚性单摆系统的混沌控制，使得系统稳定运行在目标轨道。Wheeler等[11]将开环加闭环控制方法应用于有效神经元系统，作为从混沌吸引子中提取稳定极限环的方法，用以模拟记忆搜索和检索的状态。王杰等[12]在开环加闭环控制的基础上，针对任意m次多项式提出了一种开环加非线性闭环组合的控制方法，实现了系统的解到任意给定目标的输运，并证明其传递域是全局稳定的。陈立群[13]将开环加非线性闭环方法应用于强迫Duffing系统和Van der Pol等系统，证明了传递域的全局性。

本文以具有柔性基础的准零刚度隔振系统为研究对象，分析共存吸引子及其吸引域，并应用开环加闭环控制方法实现了系统的吸引子迁移控制，使系统由振幅大的吸引子迁移至振幅小的吸引子上，从而实现减振降噪，并对控制的稳定性进行了分析，得出目标轨道函数是全局稳定的。

1 吸引子共存分析

图1柔性基础准零刚度隔振系统Fig.1 The quasi-zero-stiffness vibration isolation system with flexible foundation

有研究表明，如果弹性体的第二主频率比第一主频率大一倍，那么只取第一阶模态也能取得较精确的结果，梁和平板的主频率分布常能满足上述条件[14]。因此，在只取一阶模态的情况下，平板或梁式柔性基础可以简化为单自由度系统来进行研究[15]。柔性基础准零刚度隔振系统结构示意图如图1所示，kqzs和k2分别表示准零刚度隔振器的非线性刚度和基座的等效刚度；c1和c2分别表示准零刚度隔振器的阻尼和基座的等效阻尼；Y1和Y2分别表示被隔振物体的位移和基座的位移；m1和m2分别表示被隔振物体的质量和基座的等效质量；Fcos ΩT表示激励力[16]。以向上为正方向，可得

取w=0.5，G=0.1，ξ1=0.05，ξ2=0.15，ω=1.6。由图 2 所示共存吸引子的相图可知，当f=6.5 时，系统存在一个周期3吸引子和一个周期1吸引子，其中“+”表示庞加莱映射点。在相空间中分别选取截面为分析平面，作如图3所示的系统吸引子及其吸引域图，其中黑色区域表示周期1运动的吸引域，白色“o”为周期1吸引子；灰色区域表示周期3运动的吸引域，白色“+”表示周期3吸引子。图3中出现了周期3吸引子在周期1吸引域中的情况，这是因为图3显示的只是周期 3 吸引子分别在所选截面上的投影，在完整的相空间中，周期3吸引子是不会出现在周期1吸引子所属的吸引域中。

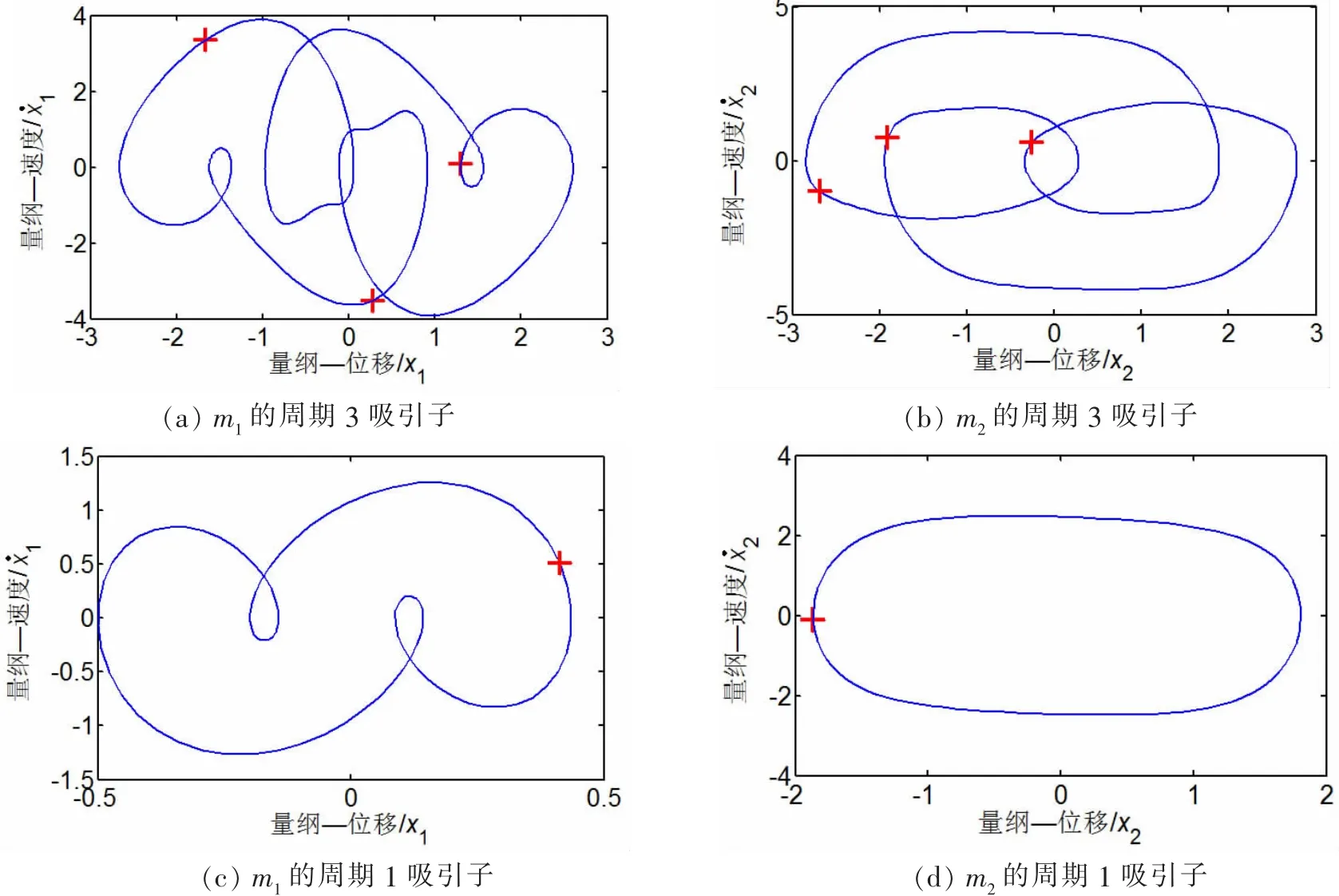
图2共存吸引子的相轨迹及其庞加莱映射点Fig.2 The phase trajectories of coexistent attractors and their Poincare mapping points

图3共存吸引子及其吸引域Fig.3 Coexistent attractors and their basins

2 柔性基础准零刚度隔振系统的迁移控制律

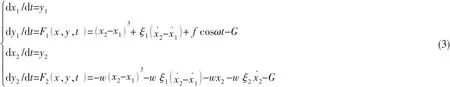
第二种方法是开环加闭环控制方法，引入开环加闭环控制律可得

3 吸引子迁移控制

由图2可看出，系统的周期1吸引子较周期3吸引子振幅小。由于初始条件不确定，系统有可能运行在振幅大的周期3吸引子上。这时，可通过设置比周期1、周期3运动振幅都小的目标轨道函数，施加控制使系统迁移至目标轨道，并沿目标轨道运行，这样可以减小系统振幅。

对于系统（3），选取目标轨道

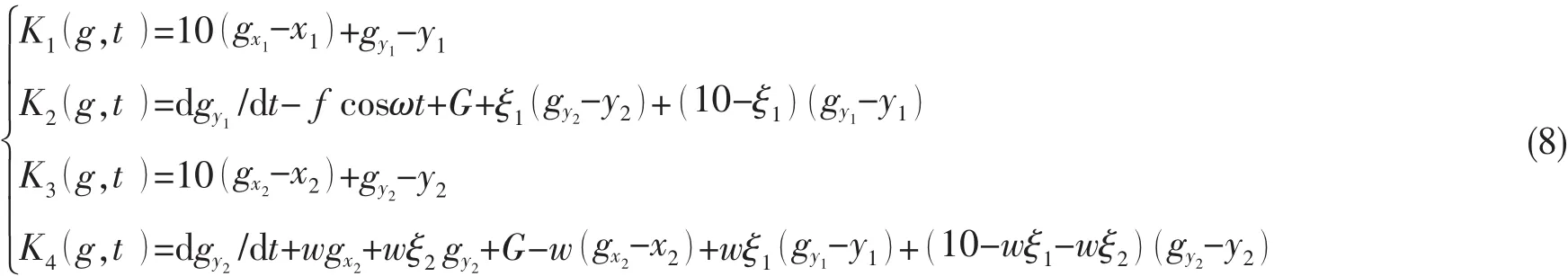
仍选取上节的系统参数，开关函数设置为当时间t＞200 s时，S（）t=1。

不同控制作用下系统的相轨迹如图4所示，黑色实线表示施加控制前系统的运行轨迹，灰色虚线表示施加控制后系统的运行轨迹，下同。由图4（a）和图4（b）可以看出，施加开环加闭环控制后系统被准确地迁移至目标轨道。若只施加开环控制，以m2为例，如图4（c）所示，可以看出施加控制后m2运行轨迹混乱无序，无法被迁移至目标轨道。

图4不同控制作用下系统的相轨迹Fig.4 The phase trajectory of the system under different control methods

上述控制方法虽然可以实现减振降噪，但存在消耗能量大的问题，且未考虑稳定性。针对这些问题，可采用另一种迁移控制策略，即在两个吸引子的吸引域之间建立一条目标轨道，当系统运行至目标轨道附近时，启动控制，系统沿着目标轨道被迁移至周期1吸引子的吸引域，此时关闭控制，系统会运行在周期1吸引子上，振幅较施加控制前变小，从而达到减振降噪的目的。

通过对Beats1进行优势分析，我们不仅是对网络音乐电台的运营模式进行剖析，更多的是从中得到其开发运营音乐产品的理念和方向。在面对如唱片、录音带、电台和电视等传统媒介时，我们应当正确对待其产品价值，取长补短，相互结合，在创新过程中注重将传统与流行相融合，为未来音乐产业的发展提供多样化路径。

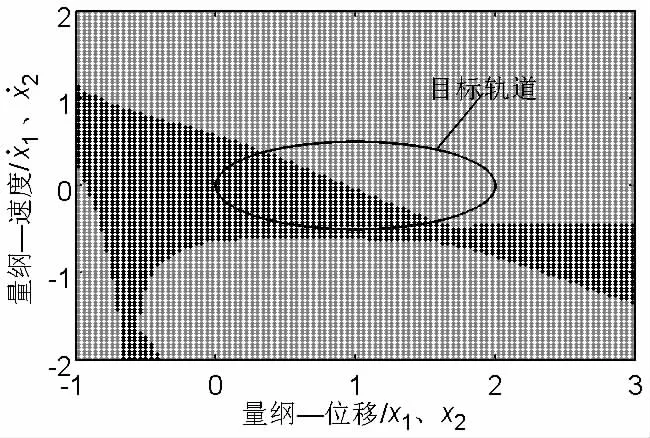
图5吸引子及其吸引域图Fig.5 Attractors and their attractor domains

图3所示的点映射图分别是在x2=0，x˙2=0和x1=0，x˙1=0 的前提下画出的。所以当x1，x˙1，x2，x˙2都位于图上周期1吸引子的吸引域内时，系统未必在周期1吸引子上运行。仍选取上述矩阵A及目标轨道函数（7）。因x1、x2的目标轨道函数相同，y1、y2的目标轨道函数相同，所以当系统被迁移至该目标轨道时，满足x1=x2，y1=y2。故可在-4＜范围内画出系统的点映射图。如图5所示，黑色区域表示周期1吸引子的吸引域，灰色区域表示周期3吸引子的吸引域，可以看出目标轨道函数连接两个吸引子的吸引域。设置开关函数为：若系统运行在周期3吸引子上，启动控制，即令S（）t=0；系统被迁移至目标轨道后，且系统运行至图5上的周期1吸引子的吸引域内时，关闭控制，即令S（）t=0。

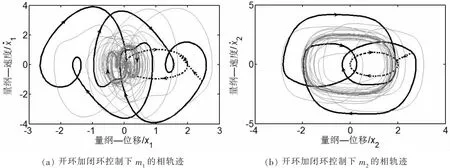
图6开环加闭环控制下系统的相轨迹Fig.6 The phase trajectory of the system under open loop plus closed loop control

系统相轨迹如图6所示，黑色实线表示施加控制前系统运行轨迹，黑色虚线表示施加控制后关闭控制前系统运行轨迹，灰色实线表示关闭控制后系统运行轨迹。可以看出，系统一开始运行在周期3吸引子上，启动控制后，系统被迁移至目标轨道，当系统运行至周期1吸引子的吸引域内时，关闭控制，系统经过短暂的瞬态过程，重新运行在周期1吸引子上。如图7所示是m1振幅随时间变化的曲线，可以看出m1较控制前振幅变小，从而达到了减振降噪的目的。

图7开环加闭环控制下m1的时程Fig.7 The time history of m1under open loop plus closed loop

4 稳定性与可行性分析

令x（t）=g（t）+u（t），代入（5）式且当S（t）=1时可得

在F（g+u，t）处进行展开

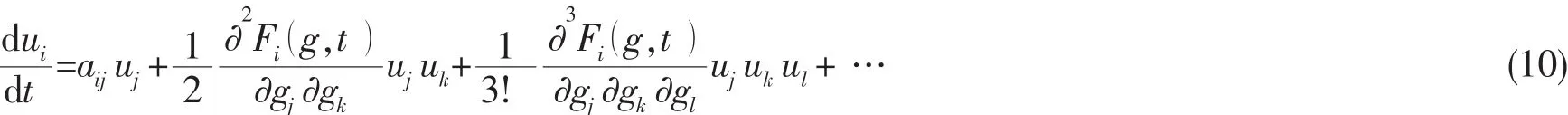
代入（4）式可得

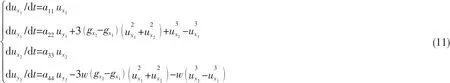
因a11=a22=a44=-10＜0，所以当时间t趋于无穷时ux1，uy1，ux2，uy2全部趋于零。故目标轨道函数的传输域是全局的，即当系统处于任何状态时都可施加控制使其迁移至目标轨道。

由上述可知，只要恰当选取矩阵A和目标轨道函数g（t）（A须为负定的对角常数矩阵，g（t）须连接两个共存吸引子的吸引域），即可保证吸引子迁移控制的稳定性，确保系统被迁移至目标轨道，并沿着目标轨道在共存吸引子之间迁移，实现减振降噪。对系统施加吸引子迁移控制的前提是存在共存吸引子，工程实际中，隔振系统工况较为复杂，极大可能存在吸引子共存现象。开环加闭环控制率可尝试采用作动器实现，控制开关可由继电器和位移传感器等构成。