基于车轮强度快速评价系统的动车组车轮强度评估

胡海涛， 王玉光

(中车青岛四方机车车辆股份有限公司， 山东青岛 266111)

车轮是铁道车辆转向架最重要的承载部件之一。其可靠性将直接影响车辆运行安全性。对车轮各个部位的应力状态和安全评定进行研究将有助于车轮的设计以及加工工艺的改进，以提高车轮的抗疲劳性能[1]。

车轮的强度评价过程需要人工进行三维建模、网格划分、载荷施加、仿真工况计算、结果后处理、出具计算报告等。此外，在设计过程中，为得到更优的设计结果，往往需要反复对车轮进行强度评价，整个过程耗时较长[2-3]。同时，准确理解强度校核方法以及熟练掌握有限元分析软件，对一般车轮设计人员而言具有一定难度，这制约了车轮的设计研发效率，增加了人为计算误差。

基于此，为了提高设计效率，减少人为误差，开发了一套基于参数化建模的车轮强度快速评价系统。同时，利用该系统，在考虑了最大过盈量及离心力影响的条件下，对15.45 t和16 t两种不同轴重的动车组动车全磨耗车轮进行静强度及疲劳强度评估。研究轴重变化对于车轮载荷及强度评估的影响，进而指导车轮设计。

1 车轮强度快速评价系统

根据UIC 510-5[4]等标准，采用Matlab、ANSYS APDL和C#3种语言混合编程的方式对车轮强度快速评价系统进行开发。在使用该系统过程中，用户可脱离有限元软件界面，无需进行三维建模，只需要输入车轮参数，系统自动实现参数化建模、自动求解，并对用户设计的车轮进行强度评价，根据评价结果指导车轮设计。

本系统由4个模块组成：

①设计参数输入模块；

②有限元仿真计算模块；

③仿真结果后处理模块；

④评价结果输出模块；

模块①的主要功能是从数据库中获取设计参数,参数主要包括：车轮几何模型参数、车轮强度计算参数、材料参数等。

模块②的主要功能是基于模块①中的数据进行有限元仿真分析，输出各个节点的节点力。该模块包含的主要内容有：根据设计参数和仿真工况建立对应的APDL(ANSYS命令流)文件，后台调用ANSYS软件执行APDL文件。

模块③的主要功能是基于模块②输出的节点数据，依照标准UIC 510-5进行仿真结果的后处理(静强度和疲劳强度评价)，并将评价结果及其对应的设计参数一起存入数据库中。

模块④的主要功能是输出模块③中的评价结果。该模块包含的主要内容有：将精简的评价结论显示在系统界面上，将详细的分析过程、分析结果以报告的形式输出。

本系统具有以下特点：

(1)自动化程度极高：用户只需输入车轮的外形参数、强度计算参数，系统自动进行参数化建模、网格划分、工况载荷计算、载荷施加、仿真计算、应力提取、结果后处理分析等一系列过程，最后自动生成计算报告。同时，数据库能统一管理设计输入参数和仿真评价结果。

(2)评价结果准确：载荷大小及施加位置，工况设置及后处理方法均按照EN及UIC标准进行，经过验证，计算结果与手动计算误差控制在1%以内。

(3)极大提高工作效率：通过应用该系统进行车轮强度计算，设计师从创建计算任务到生成计算报告比改善前手动效率提高20倍以上，极大提高工作效率。释放出宝贵的CAE资源，让用户专注于更复杂、更有挑战性的工作。

系统业务流程图见图1所示，具体计算界面见图2所示。

图1 车轮快速评价系统业务流程图

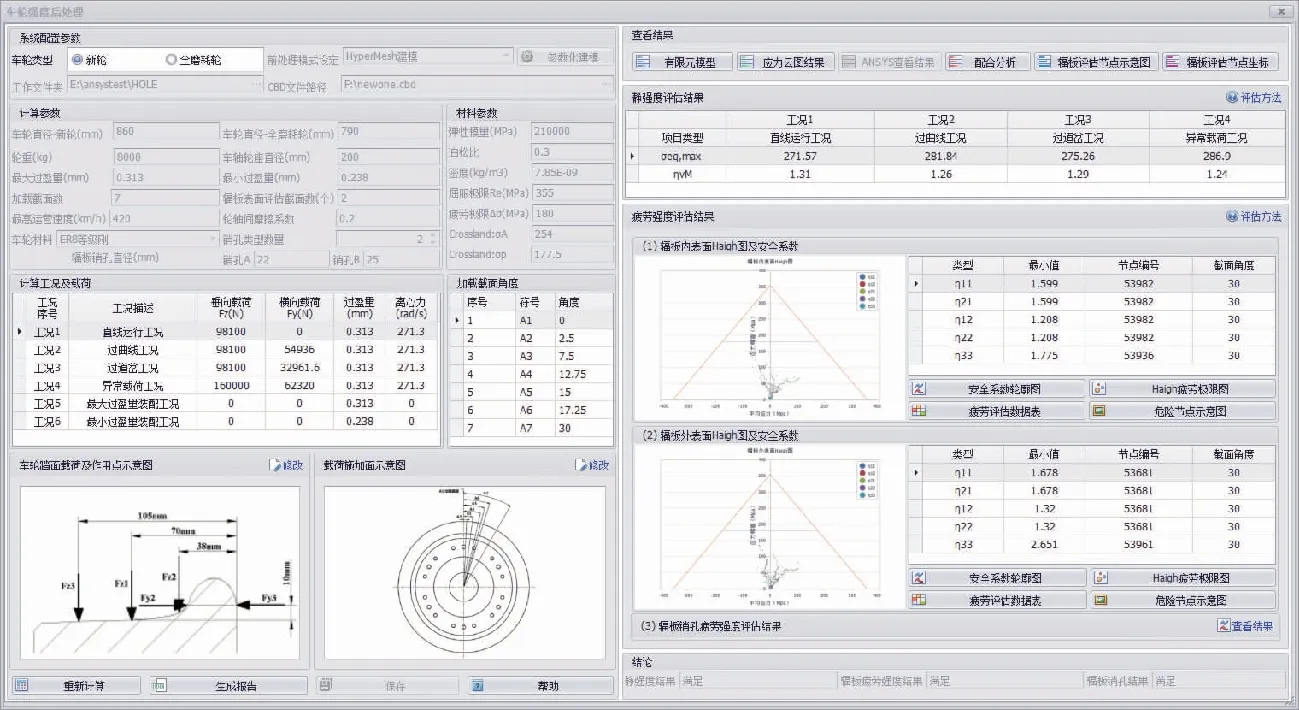
图2 车轮快速评价系统强度计算界面

2 有限元模型和工况设置

2.1 建立有限元模型

对于有制动盘安装用销孔的对称车轮，在静强度验证和疲劳强度验证计算中均采用3D有限元模型。整个车轮模型均采用ANSYS软件里的实体单元 SOLID 185。载荷以集中力的方式施加在踏面节点上。建立虚拟车轴模型，并在车轮与车轴间建立接触单元TARGE170/CONTA174模拟轮轴过盈配合。

施加绕车轮轴线的角速度以考虑离心力作用。在车轴的两端施加径向和周向约束，一端施加轴向约束。

取车轮辐板的厚度下限，参数化建立全磨耗车轮模型。图3是全磨耗轮的3D有限元模型。

图3 动车车轮有限元模型(全磨耗轮)

2.2 载荷工况

2.2.1机械载荷

依据标准EN 13979-1中所给的载荷组合和载荷施加点进行结构验证。图4和图 5中分别给出了施加点和施加面的配置方案，以下给出了载荷数值与使用组合。

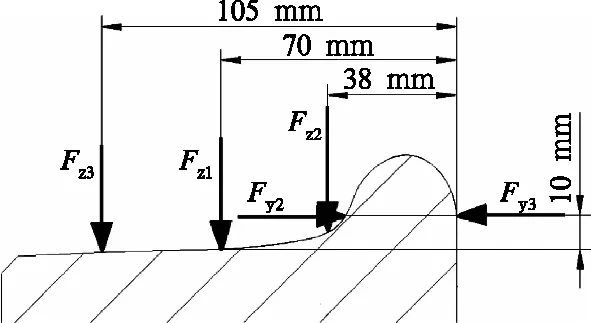
图4 车轮踏面的载荷及其施加点

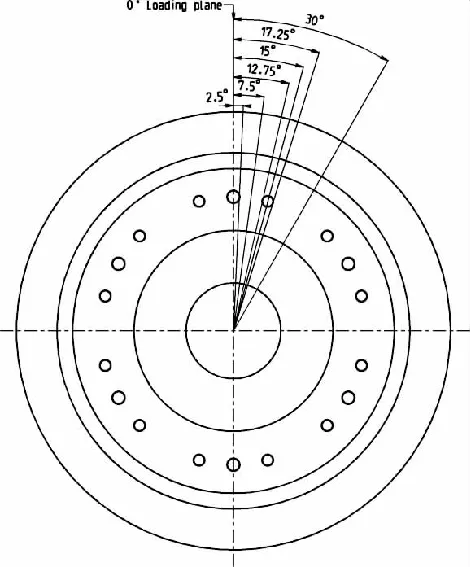
图5 载荷施加面

(1) 疲劳载荷

车轮所承受的轮轨作用疲劳载荷包括垂向载荷和横向载荷。按照直线、曲线、道岔3种工况计算各个工况载荷，载荷大小计算如式(1)～式(3)所示。

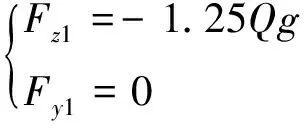
(1)

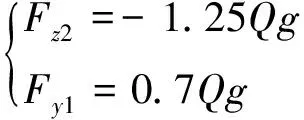
(2)

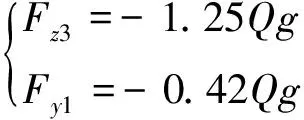
(3)

式中：Q为车轮的平均质量，kg；即轴重的一半，g为重力加速度，取值9.81 m·s-2；Fz为车轮踏面所受的垂向力，N;Fy为车轮踏面所受的横向力，N。

(2)超常载荷

依据标准UIC 510-5，超常载荷只考虑过曲线时的最大值，具体计算公式如式(4)～式(5)：

垂向力：Fz4=90 000+Qg

(4)

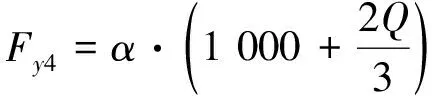
(5)

2.2.2离心力载荷

车轮上的离心力载荷按照列车最高速度(420 km/h)、车轮直径为全磨耗轮直径(790 mm)进行计算。 在有限元模型中施加绕车轮轴线的角速度以考虑离心力作用，其角速度的计算公式如式(6)：

(6)

式中：vmax为列车最高速度，km/h；d为车轮直径，mm；ω为车轮角速度，rad/s。

3 评价准则

(1)静强度：在上述3种载荷工况组合下车轮上最大Von Mises等效应力低于材料等效应力极限。

(2)疲劳强度：车轮辐板上所有节点的动应力范围Δσ应低于疲劳极限[5-6]。

关于静强度和疲劳强度，采用下面的数值：

Re=355 MPa，Von Mises等效应力的极限值(UIC 510-5)

Δσ=±180 MPa，依据EN 13979-1对车轮辐板进行疲劳验证时的，交变对称疲劳极限(应力辐板极限)

4 强度计算结果

根据第2节中的建模方式以及载荷工况设计，第3节的评价准则，利用车轮强度快速评价系统，在考虑了最大过盈量(0.313 mm)及离心力的影响的条件下，对15.45 t和16 t两种不同轴重的动车组动车全磨耗车轮进行静强度及疲劳强度评估。

4.1 静强度计算结果

(1)15.45 t轴重下的计算结果

图6～图9展示了全磨耗轮在15.45 t轴重的载荷工况下的等效应力云图，加载面角度为0°。

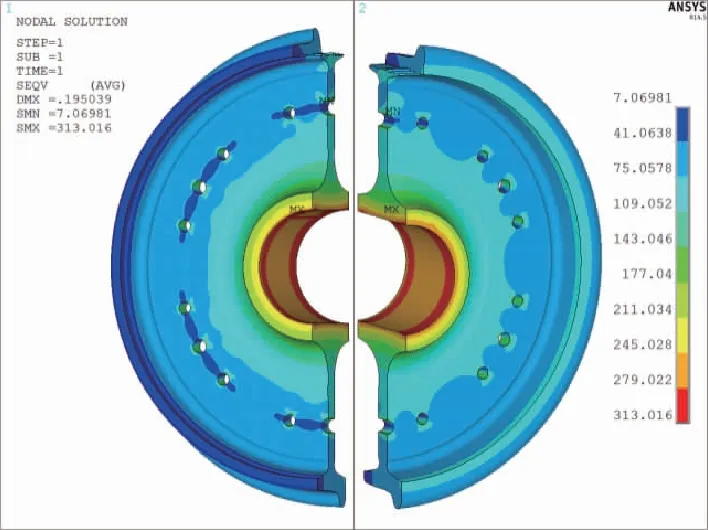
图6 直线运行:von Mises等效应力-0°加载面

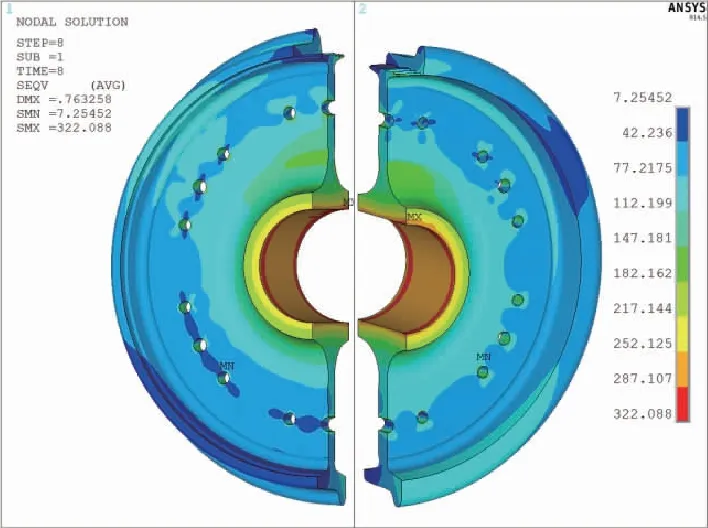
图7 过曲线:von Mises等效应力-0°加载面

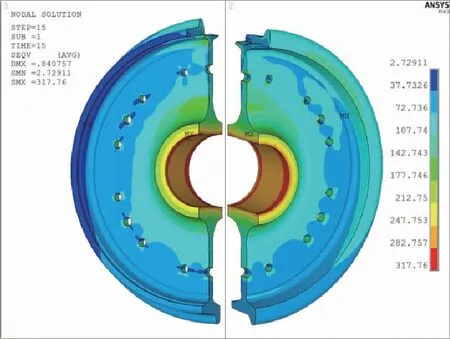
图8 过道岔:von Mises等效应力-0°加载面

(2)16 t轴重下的计算结果

图10～图13展示了全磨耗轮在16 t轴重的载荷工况下的等效应力云图，加载面角度为0°。

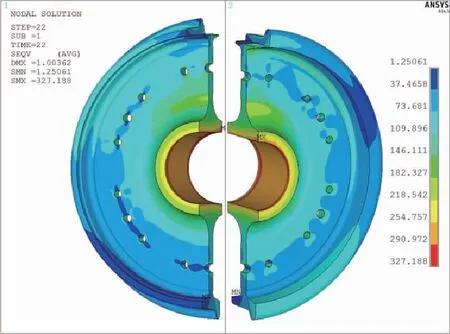
图9 超常载荷:von Mises等效应力-0°加载面

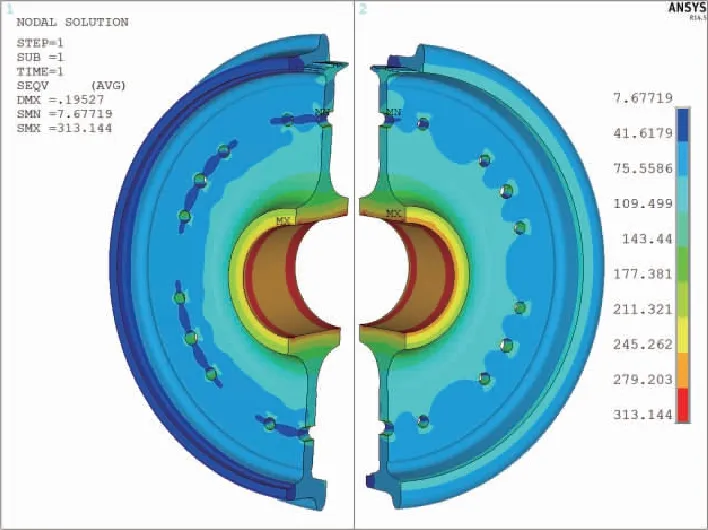
图10 直线运行:von Mises等效应力-0°加载面

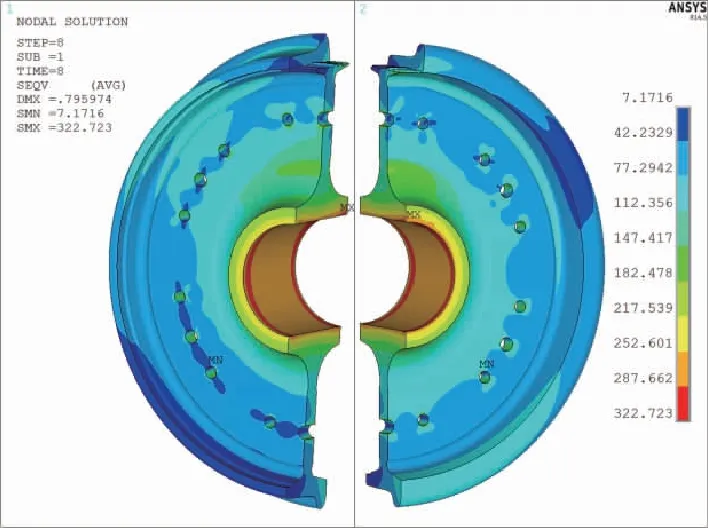
图11 过曲线:von Mises等效应力-0°加载面

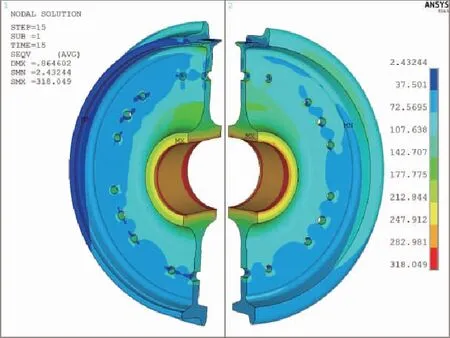
图12 过道岔:von Mises等效应力-0°加载面

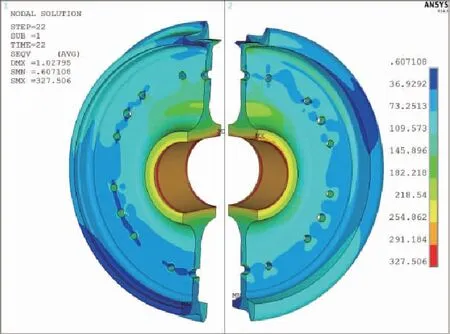
图13 超常载荷:von Mises等效应力-0°加载面

4.2 辐板疲劳强度计算结果

对0°、 7.5°、 15° 和 30° 4个位置的车轮截面上的节点，进行疲劳强度验证。将不同截面上的节点的安全系数进行比较，从而得到车轮辐板上的最小安全系数。

(1)15.45 t轴重下的计算结果

对所有考虑到的投影方向，将车轮辐板内外表面节点的σm-σa插入简明Haigh 曲线，如图14～图15所示。

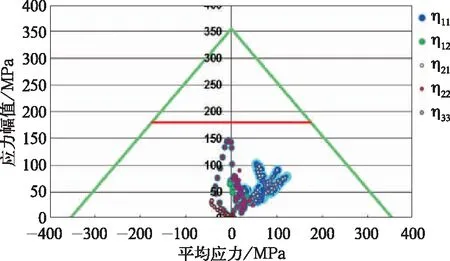
图14 关于辐板内表面上被验证节点的Haigh 图

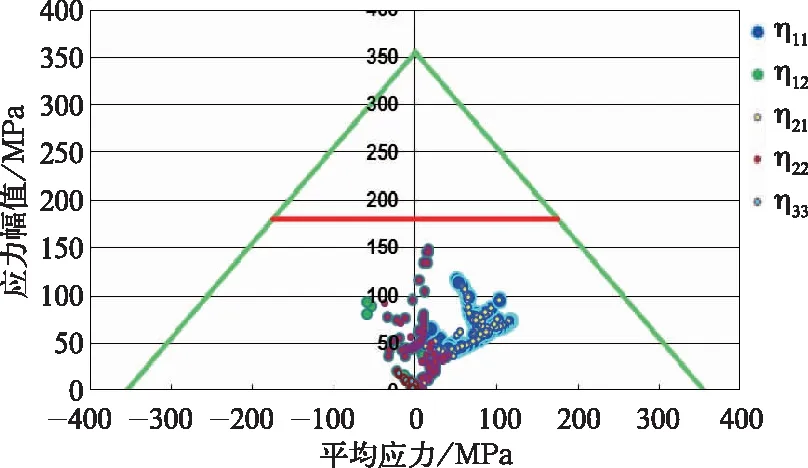
图15 关于辐板外表面上被验证节点的Haigh 图

对于车轮辐板内表面，η11(=η21)的最小值出现在节点242 733处，为1.75；η12(=η22)的最小值出现在节点446 641处，为1.24；η33的最小值出现在446 428处，为4.73。

对于车轮辐板外表面，η11(=η21)的最小值出现在节点219 759处，为1.79；η12(=η22)的最小值出现在节点446 661处，为1.22；η33的最小值出现在446 802处，为8.7。图16展示了这些节点的位置。

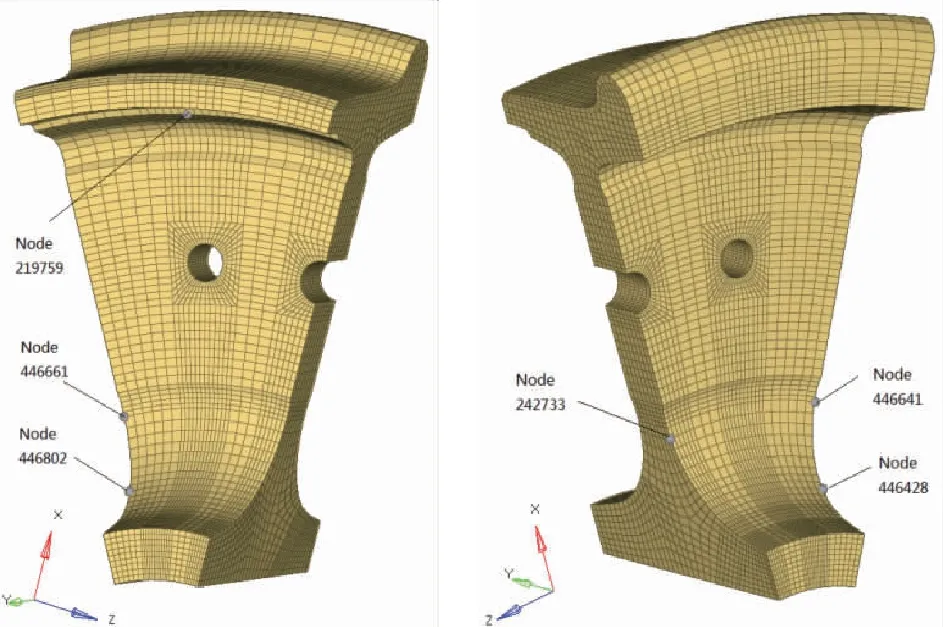
图16 车轮辐板疲劳强度验证的危险节点

(2)16 t轴重下的计算结果

对所有考虑到的投影方向，将车轮辐板内外表面节点的σm-σa插入简明Haigh曲线，如图17～图18所示。

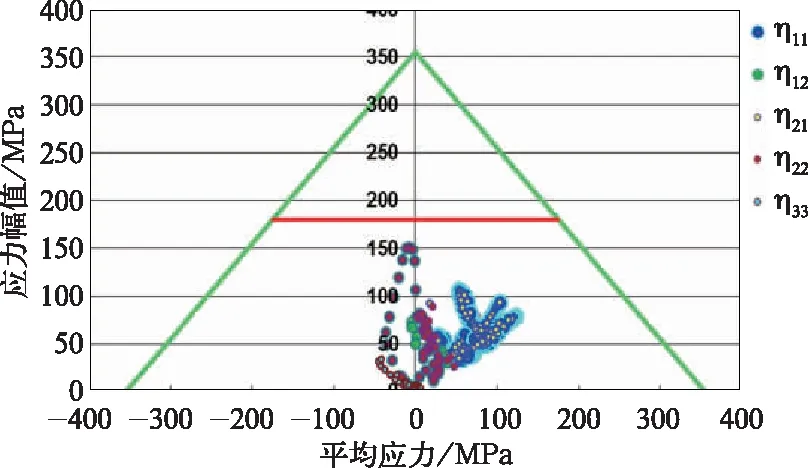
图17 关于辐板内表面上被验证节点的Haigh 图

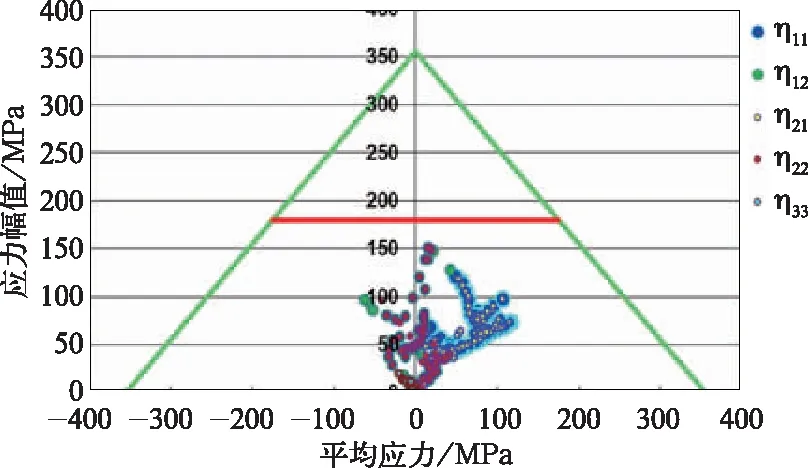
图18 关于辐板外表面上被验证节点的Haigh 图

对于车轮辐板内表面，η11(=η21)的最小值出现在节点242 733处，为1.70；η12(=η22)的最小值出现在节点446 641处，为1.19；η33的最小值出现在446 425处，为4.68。

对于车轮辐板外表面，η11(=η21)的最小值出现在节点219 759处，为1.74；η12(=η22)的最小值出现在节点446 678处，为1.20；η33的最小值出现在446 802处，为8.6。图19展示了这些节点的位置。

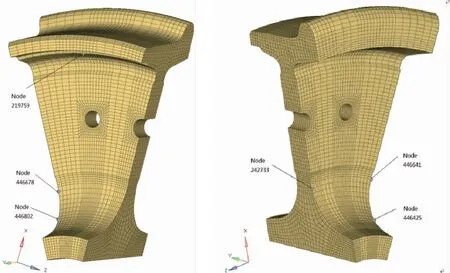
图19 车轮辐板疲劳强度验证的危险节点

4.3 15.45 t与16 t轴重结果比较

(1)载荷大小比较

表1给出了增重前后工况及对应的作用力，由表1可知，增重后对于各个工况，作用在车轮上的载荷均有增加。

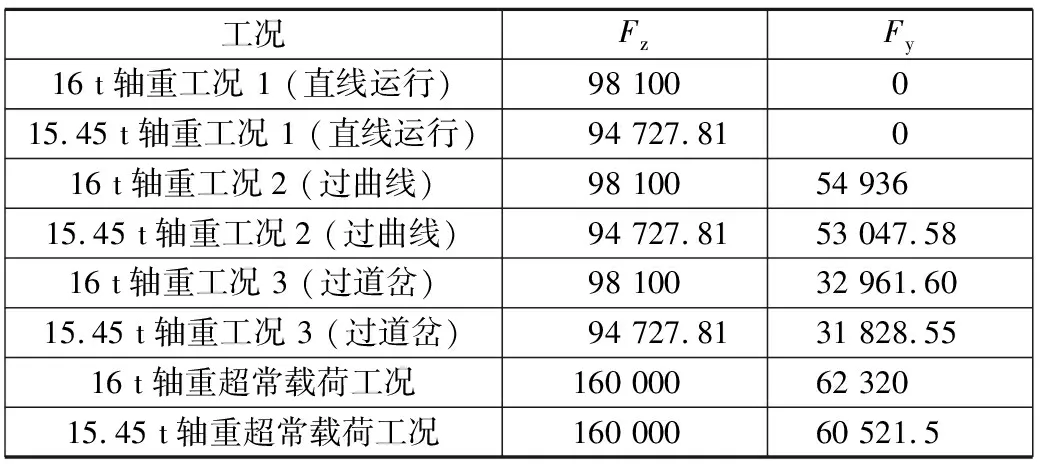
表1 增重前后工况及对应的作用力 N

(2)静强度比较

表2给出了增重前后静强度安全系数比较，由表2可知，增重后车轮在各工况下静强度安全系数均略有下降。

表2 增重前后静强度安全系数比较

(3)车轮辐板疲劳强度比较

表3给出了增重前后辐板内表面疲劳强度最小安全系数比较，由表可知，增重后车轮辐板内表面疲劳强度最小安全系数均略有下降。

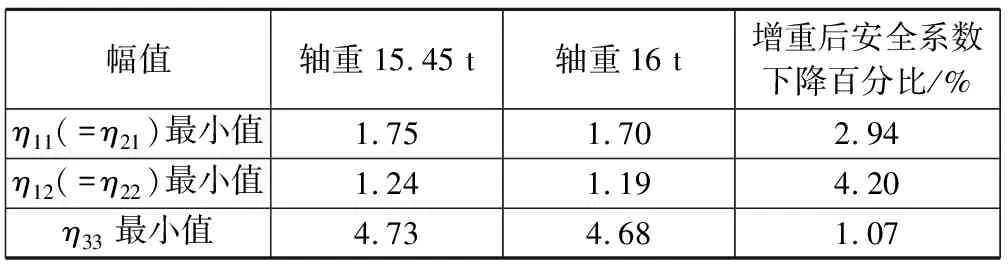
表3 增重前后辐板内表面疲劳强度最小安全系数比较

增重后安全系数下降百分比%表4给出了增重前后辐板外表面疲劳强度最小安全系数比较，由表可知，增重后车轮辐板外表面疲劳强度最小安全系数均略有下降。

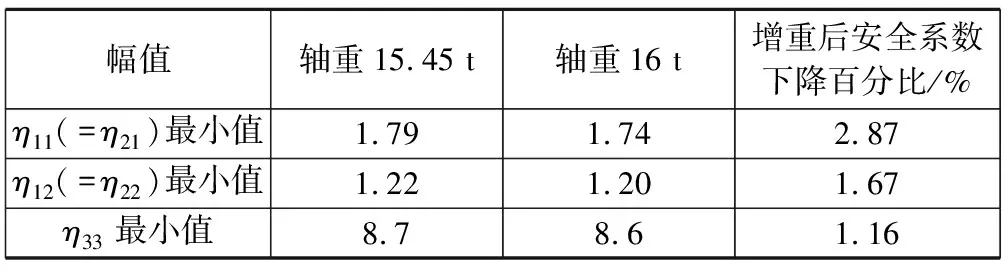
表4 增重前后辐板外表面疲劳强度最小安全系数比较

4.4 结果分析

对比结果表明，由于标准EN 13979-1中所给的载荷计算方法中，各工况载荷的大小与轴重正相关，因此车轮轴重增加后载荷有所增加。载荷的增加进而导致车轮静强度最小安全系数、车轮辐板疲劳强度最小安全系数有所减小。

因此在车轮设计过程中应控制轴重在一定范围内，防止由于轴重导致载荷增加以及车轮静强度安全系数及辐板疲劳强度安全系数的降低。

5 结 论

采用Matlab、APDL和C#3种语言混合编程的方式开发了一套基于参数化建模的车轮强度快速评价系统, 该系统能够提高车轮设计效率，减少人为计算误差。

利用自开发的车轮强度快速评价系统，对动车组全磨耗车轮进行了强度计算，计算考虑了最大过盈量及离心力的影响，并对15.45 t和16 t两种不同轴重的车轮的辐板进行疲劳强度评估。

15.45 t轴重的全磨耗轮标准计算工况下车轮最大等效应力小于许用屈服强度，最小安全系数1.085；车轮辐板内外计算节点各方向投影应力结果在Haigh图曲线内，最小安全系数1.22。

16 t轴重的全磨耗轮标准计算工况下车轮最大等效应力小于许用屈服强度，最小安全系数1.084；车轮辐板内外计算节点各方向投影应力结果在Haigh图曲线内，最小安全系数1.19。

结果表明，车轮轴重增加后载荷有所增加，车轮静强度最小安全系数、车轮辐板疲劳强度最小安全系数有所减小。因此在车轮设计过程中应将轴重控制在一定范围内。