基于轮轨蠕滑温升的机车车轮踏面优化研究

钟晓波, 陈喜红, 沈龙江, 蒲全卫

(中车株洲电力机车有限公司， 湖南株洲 412000)

轮轨型面几何匹配是机车车辆系统动力学的核心要素。轮轨几何接触特性和接触力学关系，决定了机车车辆的动力学性能和接触疲劳特性[1-2]。由于轮轨滚动接触力学行为的复杂性，使得轮轨型面匹配设计成为轨道车辆设计中的一项难题，一直困扰着国内外铁路科技工作者。车辆踏面形状先后经历了圆柱形踏面，锥形踏面直到目前广泛使用的磨耗形踏面。追求最佳轮轨型面匹配一直是各国学者孜孜以求的目标。Heller[3]等提出了将车辆动力学性能指标作为目标函数，将踏面接触点处的圆弧半径和斜率作为优化设计变量的车轮型面优化设计方法。R.K.Phlhan[4]提出了基于轮轨最佳匹配概念的机车车轮踏面外形的设计方法，提高了车辆的曲线通过性能。Shevtsov[5-6]等考虑到轮轨接触特性对车辆动力学性能的重要影响，提出了基于滚动圆半径差函数的车轮型面优化设计方法。崔大宾等[7-8]从减小接触应力的角度出发，提出了一种以轮轨法向间隙为目标的车轮踏面数值优化方法。成棣等[9-12]研究了车轮型面的多目标优化设计方法。

以上设计方法主要以车辆系统动力学及轮轨磨耗为设计目标，未考虑轮轨接触斑形态对轮轨接触温升的影响。实际上当车轮存在滑动时，轮轨摩擦温度会急剧升高，当温度超过400 ℃时车轮屈服强度急剧下降，在轮轨接触应力和轮轨牵引力/制动力的共同作用下，车轮表面材料塑性变形增加，形成圆周鱼鳞状剥离。

文中开展了以轮轨蠕滑温升为目标，车辆动力学性能为约束条件的机车车轮踏面优化方法研究，旨在提高车轮抗疲劳剥离特性。

1 轮轨蠕滑温升计算

轮轨接触斑处的蠕滑温升对踏面表面的应变剥离有重要影响。为了准确计算轮轨接触斑处的蠕滑温升，根据kalker滚动理论，并结合边界元方法计算轮轨黏滑区域和黏滑区内磨耗功率分布情况，将此磨耗功率分布作为输入热流密度，利用有限元方法可以计算出轮轨接触斑处的轮轨蠕滑温升。

1.1 轮轨滚动接触模型

轮轨滚动接触问题余能表达式如下：

SAc{hpz+(Wτ-u′τ)pτ}dS

(1)

式中，Va为整个轮轨接触体；

Aua为非接触区边界；

Ac为轮轨接触区边界；

Sijhk为材料柔性系数；

σ为应力；

h为轮轨间隙；

pz为轮轨接触压力；

Wτ为轮轨蠕滑率；

u′τ为接触区体2的边界切向位移；

pτ为接触区切向应力。

根据余能原理，滚动接触问题的解使余能取得最大值，滚动接触问题归结为求式(1)余能的最大值。图1为某踏面在0.1%蠕滑率下的滚动接触计算结果，此时接触斑前沿处于黏着状态，接触斑后端为滑动区，由于滑动引起的摩擦功分布特征如图1所示，此时接触斑前端处于黏着状态，所以磨耗功集中于轮轨接触区后部。

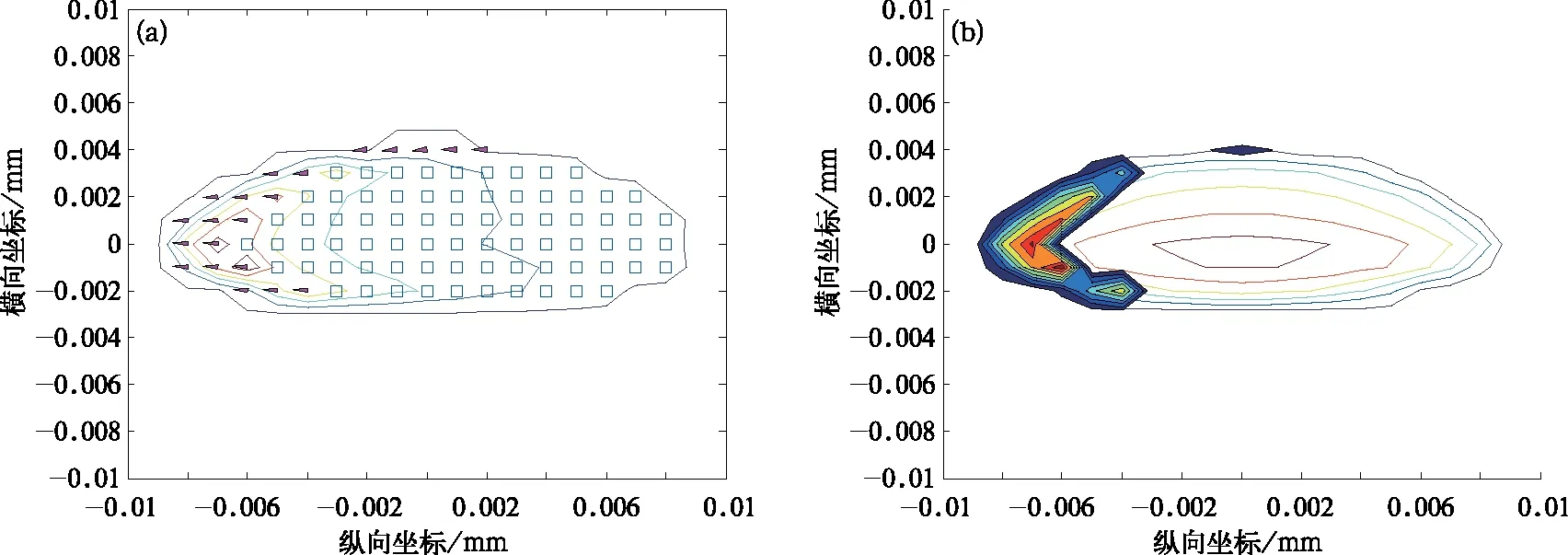
图1 轮轨蠕滑功率分布

1.2 轮轨滑动温升有限元计算模型

采用六面体单元对车轮进行网格划分，网格边长为10 mm。轮轨接触区域温度梯度较大，为提高计算精度，根据轮轨几何接触位置，将接触区域网格细化为边长1 mm的网格，如图2所示。

图2 有限元模型

图3 载荷加载

将轮轨蠕滑摩擦功率作为热流密度作为边界载荷施加到轮轨接触斑上，如图3所示，并在边界上施加空气对流换热等边界条件。为模拟车轮滚动，应使载荷沿圆周方向移动至少一个接触斑距离。图4为某机车在2 km/h滑动速度差下的轮轨蠕滑温升计算结果，可见其轮轨蠕滑温升可达到约700 ℃，车轮强度急剧下降，在轮轨纵向力作用下极易导致车轮踏面剥离。

图4 轮轨蠕滑温升计算结果

2 优化方法

2.1 目标函数

以左右轨顶公切线的中点作为坐标系原点，公切线为横坐标轴，竖直向上为纵坐标轴建立坐标系。将车轮踏面记作Z(yw)，其中yw为车轮踏面的横坐标。在给定工况下轮轨蠕滑温升高低由踏面形状完全确定。轮轨蠕滑温升记作T(Z)，它是关于踏面Z(yw)的泛函。文中的研究目的是减小轮轨蠕滑温升，因此将轮轨蠕滑温升T(Z)作为目标函数。

2.2 约束条件

车辆动力学性能指标包括直线运行稳定性、曲线通过能力、脱轨系数以及磨耗指数等性能指标。这些指标不仅与车轮型面有关，还与车辆悬挂参数有关。若直接将最终动力学性能指标作为约束条件，会使得优化模型非常复杂。实际上，通过轮轨几何接触特性，便可以判断轮对的动态性能，结合机车车辆的悬挂参数、线路条件等，最终预测机车车辆动力学性能。轮轨几何接触特性可以通过左右滚动圆半径差(记作D(y)，y为轮对横移量)表达，它一般为轮对横向位移的非线性函数。在机车车辆横向运动学方程中就包含有轮对左右车轮滚动圆半径之差，左右车轮滚动圆半径差是描述轮对与钢轨接触的最主要特性之一，对直线运行稳定性、曲线通过能力、脱轨系数、磨耗指数等性能指标有直接影响。将左右滚动圆半径差函数作为动力学性能约束条件，可以实现机车车辆动力学性能与车轮型面的直接联系，避免直径将动力学性能指标作为约束条件，简化了车轮踏面优化模型。

2.3 优化模型

以轮轨蠕滑温升为目标，车辆动力学性能为约束条件的优化模型可用式(2)描述：

(2)

式中，Dobj(y)为动力学性能所要求的目标滚动圆半径差函数。

3 踏面优化实例

JM3踏面是一种我国机车广泛使用的磨耗型踏面，主要应用于货运及客运机车。随着重载运输的发展，机车轴重不断增加，牵引及制动力不断增大，导致车轮踏面频繁剥离，严重影响机车运行安全和运行品质，极大增加机车维护费用。

3.1 JM3踏面轮轨接触特性分析

JM3踏面与轨底坡为1/40的CHN60轨在轴重25 t 时的轮轨几何匹配特性及轮轨接触应力如图5所示。

图5 JM3轮轨匹配特性

CHN60钢轨轨顶由R300、R80及R13等3段圆弧组成，其中R300圆弧为主接触区域，该段圆弧半径较大，在此区域接触时轮轨接触应力较低。而JM3踏面在对中位置时与钢轨的接触区域在R80圆弧上，导致接触应力高达1 741 MPa。JM3踏面接触斑呈椭圆状，且其长轴处于钢轨前进方向，这种形态的轮轨接触斑会引起很高的轮轨蠕滑温升。

3.2 JM3踏面优化

JM3滚动圆半径差函数斜率较低，约为0.1左右，不利于曲线通过性以及车轮磨耗均匀性。因此，将踏面优化的约束目标滚动圆半径差函数斜率提高至0.2，并适当增加轮缘根部区域的轮径差，以改善JM3曲线通过性性能。目标滚动圆半径差函数曲线见图6所示。以此目标滚动圆半径差函数为动力学性能约束条件，轮轨蠕滑温度最小为目标的优化结果如图7所示。

为保证车轮曲线通过及道岔通过安全性，优化后的踏面采用了与JM3一致的轮缘及反斜坡廓形，仅优化了图7中点G至点H间的踏面廓形。因优化后的踏面外形与JM3踏面的动力学特性在小曲线半径上并无差异，仅在大半径曲线及直线上存在差异，确保了小曲线通过安全性。

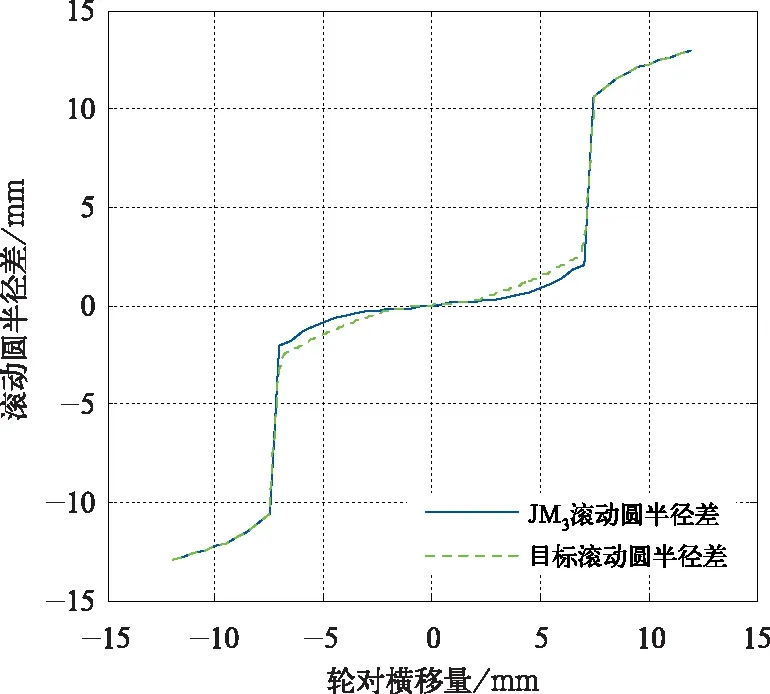
图6 目标滚动圆半径差曲线

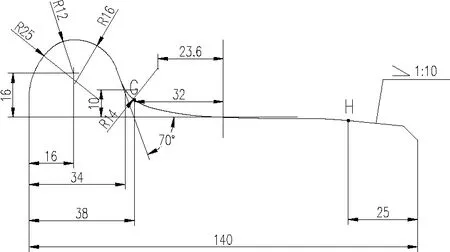
图7 JM3优化踏面

3.3 优化结果分析及讨论

3.3.1轮轨接触特性

图8、图9为JM3踏面优化后的轮轨匹配特性，轮轨接触区域分布均匀，有利于轮轨的均匀磨耗及踏面形状的维持，减小因踏面凹陷导致的维护费用。图9为车轮处于对中位置时的轮轨接触斑形状，其轮轨接触面积为199 mm，轮轨接触应力为1 011 MPa，较优化前减小42%。机车运行时，由于轮对横向运动，接触点会随之变化，轮轨接触应力也会随之变化。图10为JM3踏面优化前后不同轮对横移量时的轮轨接触应力，由图10可见，在整个踏面接触区域，优化后的轮轨接触应力均显著小于JM3踏面的轮轨接触应力，有利于减小轮轨踏面接触区域的滚动接触疲劳，提高车轮使用寿命。

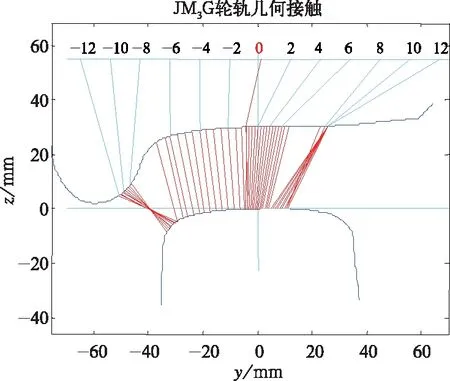
图8 JM3优化踏面轮轨匹配特性

3.3.2轮轨蠕滑温升

优化后的JM3踏面在各不同工况下轮轨蠕滑温升计算结果如表1所示。优化后的车轮踏面轮轨蠕滑温升显著下降，优化踏面在3 km/h滑动速度差下的轮轨蠕滑温升基本小于400 ℃，能够显著改善车轮踏面材料因升温软化引起的塑性变形累积疲劳剥离。

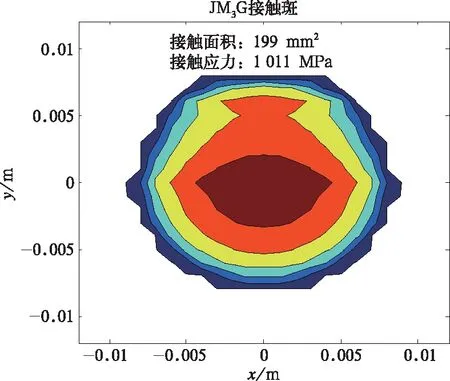
图9 JM3优化踏面轮轨匹配特性

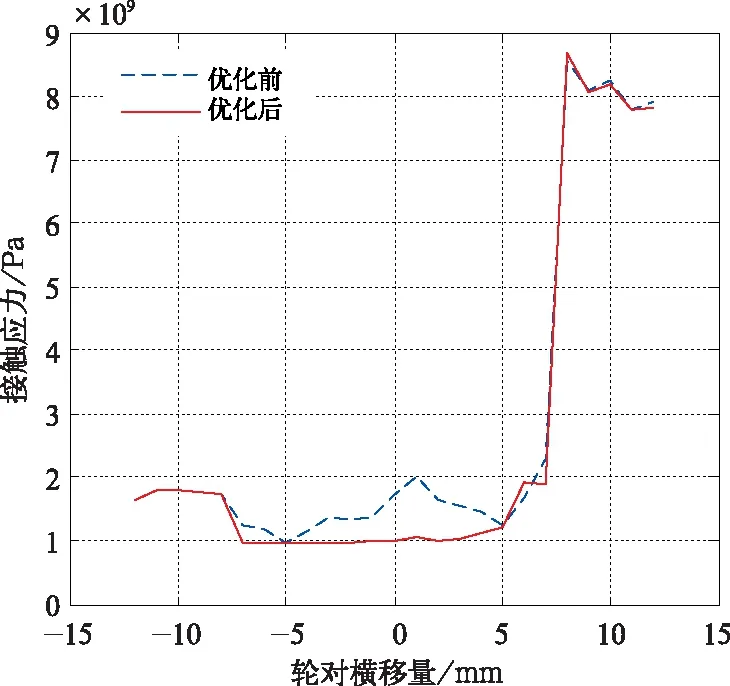
图10 JM3踏面优化前后轮轨接触应力

表1 不同工况下的轮轨蠕滑温升

4 结 论

利用边界元——有限元方法分析了轮轨蠕滑温升特性。在此基础上开发了一种以轮轨蠕滑温升为目标，车辆动力学性能为约束条件的踏面优化方法，并开发了设计软件，能够快速有效设计出满足车辆动力学性能条件的踏面曲线库。利用最优化方法在踏面曲线库中寻找具有最低轮轨蠕滑温升的踏面曲线作为最优踏面。分析结果表明，优化后的踏面具有良好的几何接触特性，能够有效降低轮轨蠕滑温升，改善轮轨接触疲劳特性。