空间抽样中最优单元尺寸确定方法研究

张维群，尤靖琛

(西安财经大学 统计学院，陕西 西安 710100)

一、引言

空间抽样方法广泛应用于农业、人口和自然资源等领域的总体推断中，通常将研究区域按照特定方式划分成互不重叠的面积单元，形成区域抽样框[1]8-9，并采用一定的抽样方法抽取具有代表性的样本单元，利用样本信息实现对总体特征的推断。由于区域划分方式可变，所形成的不同抽样框中样本的代表性有所差异，因此，空间抽样调查结果往往受到样本单元尺寸和形状的影响。而实际应用中，单元尺寸的设计一般采用经验方法予以确定，由于区域抽样框的尺度效应，不同单元尺寸抽样框的抽样估计精度和调查成本也有所不同，科学地设计抽样单元尺寸对于提高空间抽样估计精度和节约调查成本均具有现实意义。

目前，文献对于单元尺寸确定问题的理论研究存在一些探索性的思想，给出了确定单元尺寸的思路，但并未形成科学的理论体系。在空间抽样实践中，人们首先发现了抽样框的尺度效应，认为抽样框中单元的尺寸影响着抽样估计精度，González通过对单元尺寸和估计量方差进行相关分析，提出了优化单元尺寸的思想[2]；与此同时，Carfagna和Gallgeo通过对单元尺寸与方差间的相关关系图分析，给出了优化单元尺寸的思路[3]；在空间抽样的实践中，张锦水等在对冬小麦种植面积空间分层抽样效率的影响因素分析中，也发现方差的大小与单元尺寸有着明显的相关关系，并且伴随着网格尺寸的增大，抽样方差也会增大[4]。以上文献考虑了抽样单元尺寸对总体估计有效性的影响，提出了优化空间单元尺寸的思想，但没有给出精确确定单元尺寸的数理方法，使得所确定的单元尺寸对于提高总体推断精度的效果有限。从尺度效应的内容来看，空间抽样单元尺寸不仅影响着总体估计量方差，还影响着抽样成本与样本容量等方面。王迪等利用空间自相关系数与抽样单元尺寸的关系进行单元尺寸初选，并且以相对误差、变异系数和样本容量为抽样效率评价指标，通过定量分析不同单元尺寸的抽样效率，实现对抽样单元尺寸的优选[5]。有关文献对于确定空间抽样最优单元尺寸的思路不尽相同，归纳起来有以下几方面的思想：基于遥感影像分辨率确定单元尺寸的最小下限；从调查成本角度给出单元尺寸的最大上限；基于空间分层抽样识别性考虑的单元尺寸不超过最小层面积的思想；基于空间单元独立性要求的单元尺寸确定方法。但是，文献对于单元尺寸如何影响调查成本并未讨论。此外，目前的文献通常是在指定一部分单元尺寸中选择最优，并非是单元尺寸全部定义域内的全局最优尺寸，缺乏单元尺寸确定方法的科学设计。因此，本文拟从单元尺寸对估计精度和调查成本影响入手，提出一种确定最优单元尺寸的方法，使得空间抽样方案中单元尺寸设计具有一定的科学性。

本文通过分析单元尺寸对调查成本和估计精度的影响，构造空间抽样的成本函数和样本方差统计量；结合单元标志值及其地理信息拟合标志值函数，构建成本约束下使样本方差达到最小的目标函数，以此确定最优的抽样单元尺寸；同时对目标总体进行估计，据此讨论最优单元尺寸确定方法的优良性。

二、基于抽样单元尺寸的调查成本和抽样方差

在空间抽样问题研究中，将研究区域划分为“不重不漏”的抽样单元，以形成空间抽样调查区域抽样框。研究区域可被划分成规则的格子或栅格，也可以分为不规则的抽样单元，为了方便抽样设计过程，增加实际调查可操作性，通常划分调查区域形成面积相等的正方形网格抽样框进行抽样。

(一)基于空间单元尺寸影响的调查成本函数

在传统的抽样调查中，调查成本通常分为固定成本和可变成本两部分。固定成本是指组织实施一次调查必须花费且固定不变的成本，包括调查方案设计、人员的培训等方面的费用。可变成本是随着样本容量的大小而改变的成本，包括调查资料准备、调查者劳动报酬等方面的费用。传统抽样调查的成本函数定义为：

C=C0+nC1

其中，第一项C0是固定成本部分；第二项为可变成本部分，C1是调查的单位成本，n是抽样调查的样本量。

谢邦昌认为，抽样调查的成本可以看作是样本量n、抽样单位大小x、抽样概率p和调查范围s的一个函数，即：

C=f(n，x，p，s)

成本常随着样本大小与调查范围的增大而增大；而样本内基本单位个数相同时又随着抽样单位的增大而缩小[6]24-25。

与传统抽样的成本函数相比，空间调查成本除了受到样本量的影响外，还有抽样单位大小x和调查范围s的影响。空间抽样中，抽样单位是地理空间上区域网格抽样框的每一小格，显而易见，当格子单元的尺寸增大时，抽样单位大小x随之增大，在其它因素不变的情况下样本区域的调查成本将有所提高；调查范围s对成本的影响主要体现在样本分布的疏密程度上，其它影响因素不变时，调查范围越大，样本在空间上分布越松散，在各样本点之间转移时所形成的交通成本也越高。

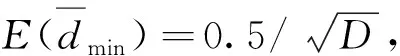
基于样本量、抽样单位大小和调查范围对空间抽样调查成本的作用机理，以及平均最近邻距离理论，构建空间简单随机抽样的成本函数为：

(1)

其中，C0是固定成本；C1是单位交通成本；a是空间区域抽样框的单元面积，na是调查的总面积；C2是调查的单位面积成本。

(二)基于空间单元尺寸的总量估计量及其方差

传统的抽样调查中，由于标志值大的单位对总体总量的影响比标志值小的单位大得多，因此使标志值大的单位具有较大的入样概率，此时所采用的不等概率抽样比采用相同概率抽样得到的估计更有效[8]。在不等概率抽样法中，比例抽样法以其实施方便、数据处理简单的特点，广泛应用于实际抽样调查[9]。使用比例抽样法时，样本大小的度量常与研究标志的某个辅助变量的值有关，单位被抽取的概率与辅助变量的大小成比例，如短时间内地区的劳动力、资本等生产要素不会发生大的变化，所以可以将某一时期的地区生产总值作为下一期经济抽样调查的参考。一般情况下，空间单元的标志值与其单元面积呈现正向关系，单元面积大的抽样框中各单元标志值的水平整体比小尺寸抽样框的标志值高，抽样估计时，不同尺寸单元的标志值对于目标总体的影响不尽相同。因此，遵循不等概率抽样中“标志值大的单位具有较大入样概率”的思想，将空间单元面积的大小作为辅助指标，以衡量单元指标值对总体总量的影响，采用放回抽样法进行抽样，则有总体总量的无偏估计量为：

(2)

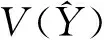
(3)

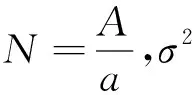
三、成本约束下空间抽样最优单元尺寸的确定方法

(一)样本量的确定

遵循传统抽样理论中“控制成本，使方差达到最小”的最优决策思想，为了使方差尽可能小，从式(3)中可以看出，当单元面积为a时，增加样本量n能够有效降低总体估计量的方差，但由于调查经费的限制，样本量不可能无限增大。当成本固定为CT时，样本量n随抽样单元面积a的变化而改变，记可变成本为Cv=CT-C0，由式(1)可得样本量：

(4)

显然，式(4)表明样本单元尺寸大小也影响着样本量的大小，故取给定预算下的最大样本量用以估计总体，此时的总体总值估计量即为抽样单元面积为a时的有效估计。

(二)空间抽样最优单元尺寸的确定

当单元尺寸较大时，各个面积单元内总量指标值较大，同时由于空间单元的异质性特征，即使面积相同的单元，在不同地理位置上所表现的观测值也不同，因此面积抽样框中各单元的标志值Yi可以用关于经度值Z1、纬度值Z2和单元尺寸(面积)a的函数来表示，即Yi=Y(Z1，i，Z2，i，a)，结合式(4)，得样本方差：

(5)

当总成本控制为CT时，单元尺寸a的变化会引起抽样样本方差的变化。样本方差值较小时，在一次抽样中估计值落在总体真值附近的概率较大，此时估计的精度也就越高。因此，固定总成本时使样本方差达到最小值的抽样单元尺寸即为成本约束下最优单元尺寸。对式(5)关于a求偏导，令导函数等于零，有：

(6)

(三)抽样单元标志值函数的建立与参数拟合

由于面积抽样框中各单元的值yi是关于其经度值Z1、纬度值Z2和单元尺寸(面积)a的函数，即Yi=Y(Z1，i，Z2，i，a)。假设Yi=Y(Z1，i，Z2，i，a)是关于各参数连续可导的函数，通过泰勒展开可表示为一个无限多项式，不妨令Yi=Y(Z1，i，Z2，i，a)近似为二次多项式：

(7)

(8)

(9)

四、空间抽样最优单元尺寸确定方法的应用

生产要素的空间分布往往呈现不均衡的特性[10]。经济活动的本质是追求利润的最大化，这驱使了生产要素和经济活动在地理空间上的流动。生产要素的流动造成了不同地区经济活动的空间关联，即空间维度上的交互作用[11]。它是区域经济发展的重要影响因素，从经济学角度出发，人们更倾向于将这种交互作用称为空间溢出效应[12]。经济学研究中，通常将行政区划作为研究的基本单元[13-17]。假定在单元内的生产要素是同质的，然而实际情况并非如此，即使在同一行政区域内，不同地区的生产要素结构也有所差异。一般来说，距离近的地区生产要素结构具有较强的相似性，这种相似性随着距离的增大逐渐减小。如果以行政区划作为研究的基本单元，往往会将相似度高的区域划分到不同的单元内，影响经济问题的分析。此时，若基于以规则网格划分地理区域形成的基本单元进行研究，可以很大限度上保证单元内生产要素的同质性，有利于准确分析经济学机理。

(一)数据来源与预处理

本文数据源于2015年陕西省107个区县的地区GDP，总体总量为17 687.84亿元。用ArcGIS处理地图时，以陕西最南纬度线与最西经度线的交点为坐标原点，建立抽样方案设计的坐标系，此时坐标原点对应基础坐标系点(264.89，3 510.20)，单位为千米，即U=264.89km，V=3 510.20km。由于陕西省的行政区划并非规则的正方形网格，往往存在一个抽样单元横跨多个区县或者一区县被分为多个抽样单元的情况，此时该区县的地区生产总值并不等同于这一个或多个抽样单元的观测值。因此，对于每一个抽样单元，以其覆盖的各区县面积占该区县的总面积为权重，定义多个区县地区生产总值的加权平均数为此抽样单元的标志值，表示为：

(10)

其中，Yi抽样单元包含了k个区县的区域，sj为该抽样单元中第j个区县所占的面积，Sj为第j个区县的总面积，GDPj为第j个区县的GDP值。以20×20km2的正方形网格抽样框为例，抽样单元数据分布如图1。

图1显示，就地区生产总值的整体水平而言，关中地区的地区生产总值最高，陕北地区次之，陕南地区的地区生产总值最低。就地区生产总值的空间格局来看，陕西省各个城市市辖区的地区生产总值较高，抽样单元GDP随着与各市辖区的距离增大呈逐渐减小的趋势，说明陕西省各市辖区的经济发展对其周边地区的经济有一定的带动作用。

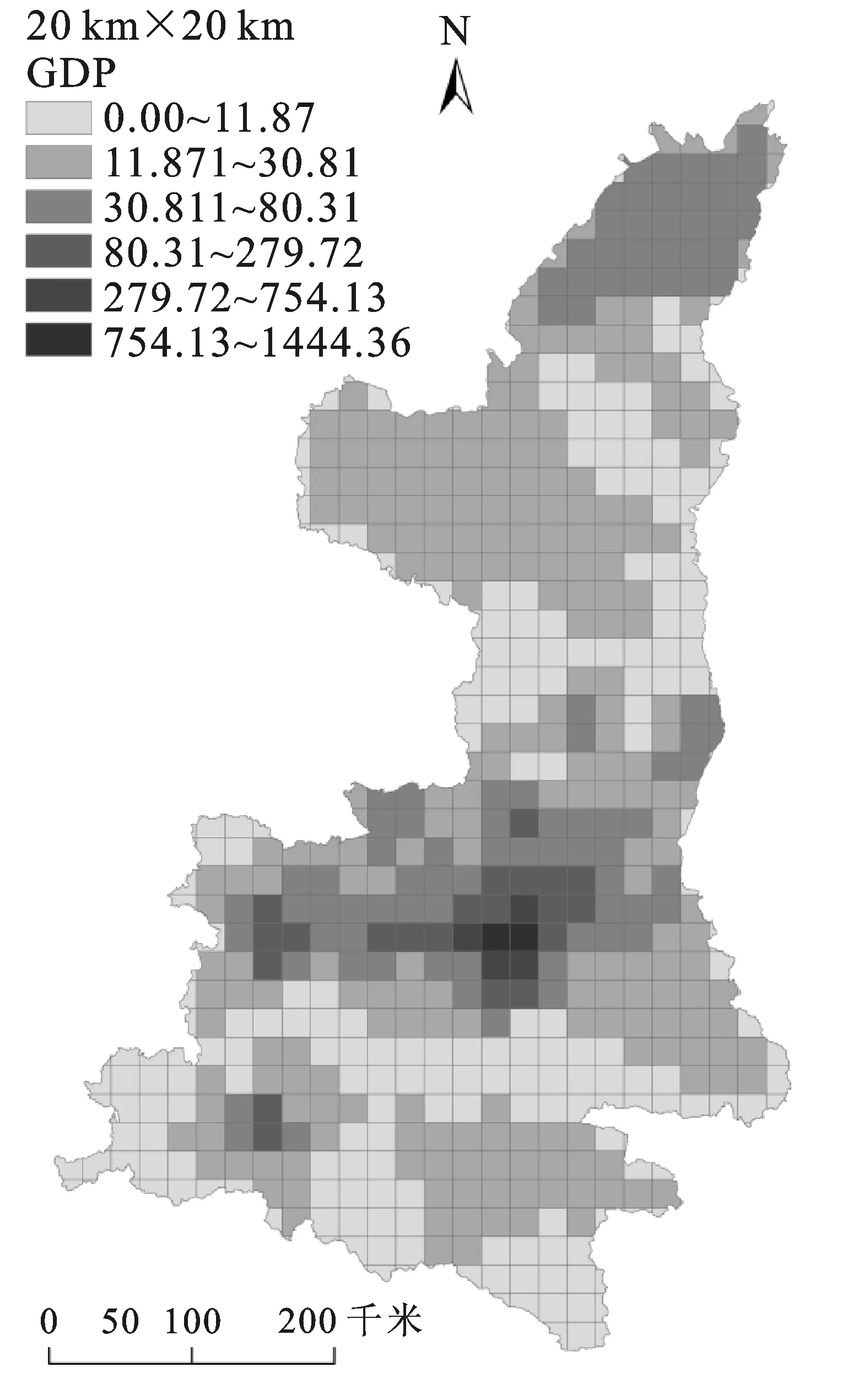
图1 2015年陕西省地区生产总值空间分布图

(二)成本控制下最优单元尺寸的确定

在陕西省地图的基础上，用大小相等、整齐排列的正方形网格分割地图以形成区域抽样框，其中的单元面积从25km2至2 700km2，共形成50个水平的抽样框。根据式(10)定义每种水平区域抽样框中各抽样单元的指标值，并记录每一个抽样单元的中心经度值、中心纬度值和单元面积，拟合得标志值函数：

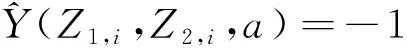
(11)

式(11)显示各样本单元的标志值随着纬度的升高和单元尺寸的扩大呈增大的趋势。根据式(8)、式(9)，得到：

(12)

(13)

不妨令总成本CT为10 000，固定成本C0为500，单位交通成本C1为2，单位面积成本C2为1。若总成本只能够调查一个样本，得maxa=9 046km2。将各成本参数代入成本约束下确定最优单元尺寸关系式(6)，结合式(12)、式(13)，解得最优抽样单元尺寸a=220.851 1km2(如图2)；根据式(4)，有样本量ns=31。

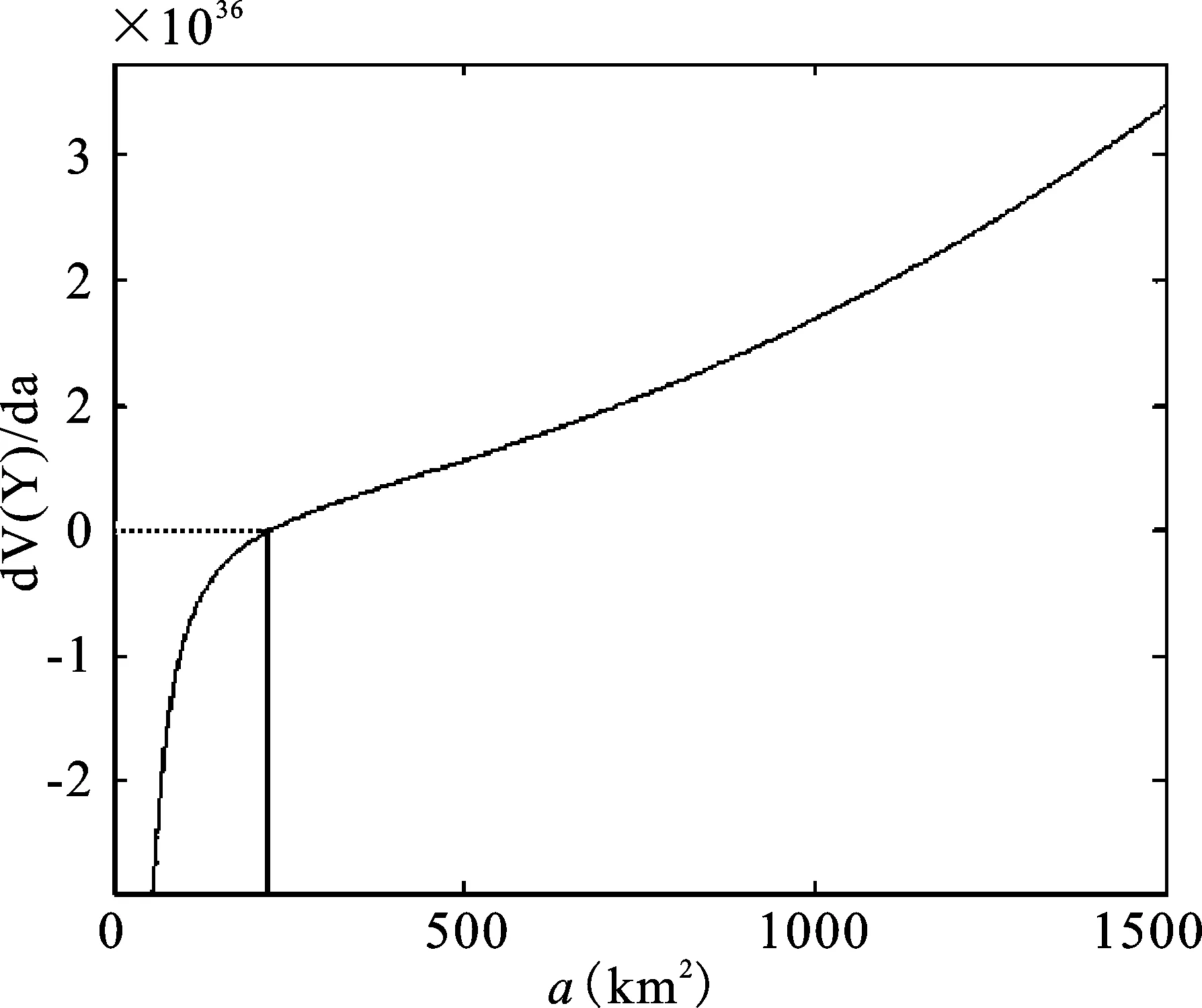
图2 总体总值样本方差关于抽样单元尺寸的偏导函数图

(三)最优单元尺寸与其它尺寸下空间抽样效率对比

为了避免地图制图误差对抽样效率的影响，在最优单元尺寸面积的基础上分别加减30km2和60km2，以新的单元尺寸划分陕西省2015年地区生产总值，以形成新的区域抽样框。在成本约束下，分别计算基于各面积抽样框的成本、样本量、总体总值估计量、相对标准误及其方差，结果如表1。

表1显示，在相同的成本约束下，基于最优单元尺寸220.8511km2所构建的空间区域抽样框对于陕西省地区生产总值的估计精度明显高于非最优单元尺寸的抽样框。同时可以看出，由于空间抽样调查的总成本限制，随着抽样单元尺寸的扩大，样本量逐渐减小，导致在各样本间转移所花费的交通成本减小，但调查的面积成本有所增加。

表1 最优单元尺寸与其他尺寸下空间抽样效率对比

(四)最优单元尺寸下空间抽样与传统抽样效率对比

将陕西省地图数据划分为面积为220.851 1km2的正方形网格，形成面积抽样框(共1 078个单元)。为了评价最优单元尺寸下空间简单随机抽样的效率，以各区县的纬度值为主关键字按升序排列、以经度值为次关键字按升序排列，对陕西省107个区县进行编号，以形成传统简单随机抽样的抽样框。取各区县面积的均值带入式(4)计算得成本控制下传统简单随机抽样的样本量n0=4。分别对两种抽样框下的总体总值、相对标准误及其样本方差进行估计，结果如表2。

表2 最优单元尺寸下空间抽样与传统简单随机抽样效率对比

注：平均面积比为调查面积占全省总面积的比例。

表2显示，在成本约束下，基于最优单元尺寸的空间简单随机抽样总体总值的估计量相比于传统简单随机抽样更接近于真实值17 687.7亿元，估计量的方差也远小于传统抽样下估计量的方差，说明最优单元尺寸下空间简单随机抽样具有有效性。传统简单随机抽样用各区县面积的均值进行抽样设计，但由于各区县面积差异较大，在实际调查中很难准确控制总成本，因此会出现实际调查费用超出预算成本的情况；而空间简单随机抽样每一抽样单元的面积相同，可以有效地将总成本控制在一定范围内，从而体现空间抽样方案设计的经济性。若不控制调查的总成本，取相同的样本量时，空间简单随机抽样的估计精度仍高于传统简单随机抽样，且调查的总成本远小于传统抽样方式。实际调查中，空间抽样调查的面积小于传统抽样下的调查面积。综上所述，在成本约束下，相比于传统简单随机抽样，空间抽样以较小的调查面积，可达到较高的估计精度，其抽样效率远高于传统的简单随机抽样。

五、结论与展望

(一)结论

本文研究了一种基于空间区域抽样框的最优单元尺寸确定方法，并且运用到实践中验证其抽样效果，将调查单元的地理信息以自变量的形式加入到标志值函数中，体现了数据的空间特性，准确量化了地理信息对于个体影响的程度和方向；考虑空间抽样调查的特性，构造了基于单元尺寸、调查距离和调查面积等因素影响的空间抽样调查成本函数；分析空间单元尺寸对于抽样调查的估计精度和调查成本的影响，提出了成本约束下确定最优单元尺寸的方法，对于提高空间抽样估计精度具有现实意义，对空间抽样理论进行了补充。

(二)问题与展望

本文研究了成本约束下空间抽样最优单元尺寸的确定问题，为空间调查方案设计中如何划分网格区域抽样框提供了一定参考。本文成本函数的各项参数均是主观指定，成本函数假定各抽样单元的调查成本和交通成本相同，但现实中调查和交通成本往往受到地理环境、气候条件等多个因素的影响，其理论研究与实践应用存在着偏差。考虑多种因素的影响，重构成本函数，进而确定最优的单元尺寸，以及考虑多目标变量时空间抽样单元尺寸的确定等问题，需要以后进一步研究。