京津冀和长三角地区制造业生产效率的比较研究——基于Malmquist-DEA模型的全要素生产率分析

刘 潇

(1.浙江大学 经济学院，浙江 杭州 310007；2.浙江省经济信息中心，浙江 杭州 310006)

一、引言

长期以来，制造业作为工业门类中技术含量最高、份额占比最大的一类产业，一直被视为国民经济的物质基础和产业主体，历来受到学术界和产业界的广泛关注。经过多年的快速发展，中国制造业建立了门类齐全、独立完整的产业体系，规模也跃居世界第一位，但是与世界先进水平相比，中国制造业仍然大而不强，在自主创新、资源利用效率、产业结构水平、信息化程度、质量效益等方面差距明显。近年来，随着中国服务业的快速发展，不少区域和省份制造业在国民经济中的比重较以往有不同程度的下滑，全国制造业增加值占GDP的比重也由2013年的34.6%下降至2016年的28.8%。众多国内外学者研究发现，发展中国家自身的去工业化会给本国经济带来严重的负面影响，认为工业化在发展中国家经济发展进程中仍然扮演着至关重要的角色。在中国产业结构服务化进程不可逆转地向前推进而工业化进程却尚未结束的大背景下，推动制造业尤其是先进制造业高质量发展不仅是构建现代化产业体系的必由之路，而且是提高全员劳动生产率、避免产业空心化进而跨越“中等收入陷阱”的破题之举，为此对制造业生产效率开展研究以评判其增长绩效和发展质量显得颇具现实意义。

国际上，全要素生产率(Total Factor Productivity，TFP)通常被视为衡量经济体或产业生产效率最有效的经济指标，尽管国内一些学者基于国情对用全要素生产率衡量中国经济或产业生产效率有不同看法，但这并不影响全要素生产率在国内众多生产效率评价场景的广泛使用。然而，目前国内关于制造业全要素生产率的测算研究多以全国或省级区域为研究样本，跨省际区域的研究偏少，而仅有的文献大多选取的数据较为陈旧，不能及时反映近年来产业最新发展状况，或者仅对制造业整体进行生产效率评价而未就具体行业类别展开深入分析。此外，由于中国制造业在不同区域的发展并不均衡，对发展差异较大的区域进行比较研究的现实指导意义有限。为此，本文选择中国工业化进程相对领先、制造业较为发达且发展阶段较为相近的京津冀地区和长三角地区作为研究对象，比较分析两大发展区域近十年来制造业全要素生产率的变化，为中国制造业生产效率领域提供一个有益的区域研究视角。

二、文献综述

全要素生产率可以理解为各要素(如资本和劳动等)投入之外的技术进步和能力实现导致的产出增加，是剔除要素投入贡献后所得到的部分。对全要素生产率开展研究不仅可以识别经济是投入型增长还是效率型增长，从而确定经济增长的可持续性，而且能够为政府制定和评价长期可持续增长政策提供科学合理的参考依据。具体来说，通过全要素生产率增长对经济增长贡献与要素投入贡献的比较，就可以确定经济政策是应以增加总需求为主还是应以调整经济结构、促进技术进步为主[1]。全要素生产率主要有参数法和非参数法两种计算思路，早期普遍使用的参数法有索洛余值法、隐回归法等，近年来使用最为广泛的参数法是随机前沿生产函数法(Stochastic Frontier Approach，SFA)及其拓展改进方法，而非参数法则是综合运用Malmquist指数和数据包络分析理论(Data Envelopment Analysis，DEA)的Malmquist-DEA法(有时亦简称为Malmquist指数法)。

早期采用较多的全要素生产率计算方法，诸如Cobb-Douglas等生产函数只反映各投入因素与平均产出之间的关系，其一重要假设是所有生产者都能实现最优的生产效率。Farrell在研究生产有效性问题时开创性地提出了前沿生产函数(Frontier Production Function)，允许实际生产效率低于最优生产效率从而放松了前述假设[2]。随机前沿生产函数即是在确定性的前沿生产函数基础上提出了具有复合扰动项的随机边界模型，目前被国内外学者广泛使用的随机前沿生产函数法大多基于Battese和Coelli的研究模型[3]。该模型对技术无效率项的数学形式和技术无效率项与随机项的概率分布作出了假设，如张乐等学者即采取此模型计算了中国农业的全要素生产率[4]。Malmquist-DEA法中的Malmquist指数最早是由瑞典经济学家Malmquist在分析不同时期消费变化时提出来的一种统计综合方法，后来Fare等对该指数的应用进行了扩展性研究以考察全要素生产率增长，并把全要素生产率的变动分解为技术进步的变动和技术效率的变动[5]，从而被广泛应用于各部门、企业甚至整个经济体生产效率的度量。Malmquist指数是一种基于距离函数定义的指数，距离函数的求解大多有赖于DEA线性规划模型，如赵伟等学者即采取此方法计算中国各省份的全要素生产率[6]。总体而言，相较于随机前沿生产函数法，尽管Malmquist-DEA法存在不具备统计特征、固定的前沿面忽略了样本之间的差异性等缺点，但其不需要对生产函数的形式做先行假设条件，不涉及投入产出的数量和价格信息，且通过一阶差分消除了样本同方向的变化从而有效地弱化了数据质量对结果的影响[7]，加之其计算过程简洁、同样适用于面板数据分析，故本文采用Malmquist-DEA法计算制造业的全要素生产率。

三、Malmquist-DEA法的全要素生产率计算模型

根据Malmquist指数原理，在t时期的技术条件下，从t时期到t+1时期的全要素生产率的变化设定为：

(1)

式(1)中Dc为距离函数，下标c表示基于不变规模报酬的距离函数，与基于可变规模报酬的距离函数Dv相对应。距离函数可以理解为全要素生产率在t时期的实际值与前沿生产面(即可能的最大值)之间的比值，值越大表示实际生产越接近前沿生产面。x表示投入变量，y表示产出变量。

同理，在t+1时期的技术条件下，从t时期到t+1时期的全要素生产率的变化可表示为：

(2)

由于基于t时期和t+1时期的技术条件定义的指数在经济含义上是对称的，故从t时期到t+1时期的全要素生产率的变化，即全要素生产率指数(TFP)，用两者的几何平均数来表示：

ΔTFP=

(3)

由于Ray与Fare等学者就技术进步指数应采取基于不变规模报酬距离函数还是基于可变规模报酬距离函数尚有分歧[8-9]，故全要素生产率指数有两种略有差异的分解形式[注]两种分解方式中，技术进步指数(ΔTP)、规模效率指数(ΔSC)和技术效率指数(ΔTE)的表达形式不同，但全要素生产率指数(ΔTFP)和纯技术效率指数(ΔPE)的表达形式仍然一致。。Lovell、章祥荪等国内外学者认为Ray等的指数分解模型更具解释力[10-11]，因为Fare等的模型中技术进步不是现实技术进步而是参照技术的进步；但江春等认为虽然Ray等的指数分解模型在微观研究层面更具说服力，但是针对宏观层面的研究，Fare等的分解模型更加贴近实际[12]。由于本文的研究对象为偏宏观的具体产业，故仍采取Fare等的指数分解模型，分解过程如式(4)～(8)所示。

ΔTFP=ΔTE×ΔTP=ΔPE×ΔSC×ΔTP

(4)

(5)

ΔTP=

(6)

(7)

(8)

根据距离函数的定义，Dc和Dv恰好是DEA理论中CCR模型和BCC模型最优值的倒数，故结合DEA线性规划方法，即可计算出前述全要素生产率指数以及技术效率指数、技术进步指数、纯技术效率指数和规模效率指数等各项分解指数。

四、数据来源、处理和计算结果

(一)制造业分类

根据最新《国民经济行业分类》(GB/T 4754—2017)，中国制造业包括大类代码从“13”(农副食品加工业)到“43”(金属制品/机械/设备修理业)的31个具体行业类别，但鉴于近十年来制造业的分类标准有所变化且部分行业类别生产规模较小，为保证不同年份的数据可比性以及结果实用性，本文参照联合国工业发展组织《2016工业发展报告》做法，基于相对于增加值和生产总值统计数据的研发强度将制造业分为低技术制造业、中技术制造业和高技术制造业三类，其中大类代码为13～24的行业被归类为低技术制造业，大类代码为25、30～33和41～43的行业被归类为中技术制造业，大类代码为26～29、34～40的行业被归类为高技术制造业[注]2006—2011年期间中国制造业行业统计分类仅有22个，2012—2016年期间制造业行业统计分类扩增到31个；橡胶和塑料制品业在联合国工业发展组织《2016工业发展报告》中被归类为中技术制造业，但鉴于2006—2011年期间该行业被纳入化学原料和化学制品制造业统计范围，为保持前后数据可比性，本文将其与化学原料和化学制品制造业皆归类为高技术制造业。。

(二)投入产出数据来源及处理

本文选取2006—2016年北京、天津、河北三省市制造业各行业数据作为京津冀地区的面板分析数据，上海、江苏、浙江三省市制造业各行业数据作为长三角地区的面板分析数据。鉴于各省市综合统计年鉴和《中国工业统计年鉴》中均仅有制造业整体而无制造业各行业的增加值数据，故选取各行业的工业销售产值作为产出变量的测度指标；同时，选取制造业各行业的资本和劳动两种要素作为投入变量。资本投入通常用资本存量来衡量，由于《中国工业统计年鉴》已给出将历年固定资产投资和折旧因素考虑在内的“固定资产合计”指标，参照前人研究方法，省去永续盘存法等换算过程，直接采用行业的固定资产合计作为资本存量的测度指标[13-14]。劳动投入量通常包括就业人数、劳动时间、劳动强度和劳动质量等，在自由市场竞争条件下，一般可用劳动者的工资报酬反映劳动投入的变化，但由于中国分配体制不合理和缺乏市场机制调节使得劳动收入难以准确反映劳动投入的变化，加之当前中国统计资料中尚无各制造业行业劳动收入的完整数据，故参考多数国内学者的研究经验，选择行业就业人数作为劳动力投入的测度指标[15]。

根据2007—2017年的《中国工业统计年鉴》，可直接获取京津冀沪苏浙六省市2006—2016年制造业各行业的工业销售产值、固定资产合计和平均就业人数数据。按照前述低技术、中技术、高技术制造业三类划分方法进行求和汇总，然后以2006年的工业销售产值和固定资产合计为基准，根据六省市历年的工业生产者出厂价格指数和固定资产投资价格指数分别对相应年份制造业各类别的工业销售产值和固定资产合计进行折算。

(三)计算结果

根据前述数据来源和处理方法，采用DEAP 2.1软件进行计算，整理后，2006—2016年期间制造业及三大类别行业各项指标年均增长率如表1所示，各地区和省市历年制造业全要素生产率指数如表2所示，其中京津冀地区、长三角地区及其区域内的六省市制造业全要素生产率指数取当地低技术、中技术和高技术制造业三大类别行业全要素生产率指数的几何平均值。

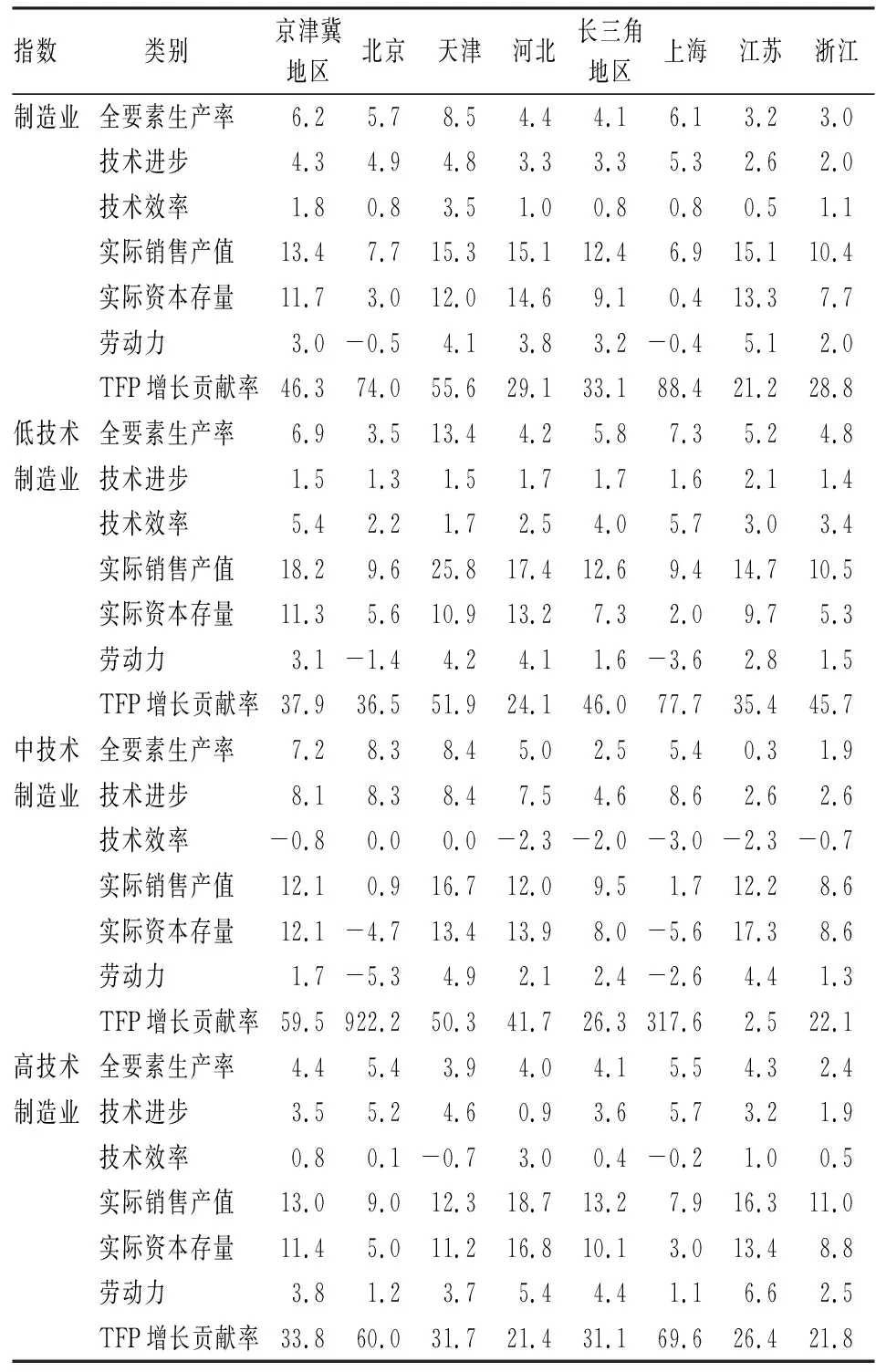
表1 2006—2016年期间制造业及三大类别行业各项指标年均增长率 单位：%

指数 类别京津冀地区北京天津河北长三角地区上海江苏浙江制造业全要素生产率6.25.78.54.44.16.13.23.0 技术进步4.34.94.83.33.35.32.62.0 技术效率1.80.83.51.00.80.80.51.1 实际销售产值13.47.715.315.112.46.915.110.4 实际资本存量11.73.012.014.69.10.413.37.7 劳动力3.0-0.54.13.83.2-0.45.12.0 TFP增长贡献率46.374.055.629.133.188.421.228.8低技术全要素生产率6.93.513.44.25.87.35.24.8 制造业技术进步1.51.31.51.71.71.62.11.4 技术效率5.42.21.72.54.05.73.03.4 实际销售产值18.29.625.817.412.69.414.710.5 实际资本存量11.35.610.913.27.32.09.75.3 劳动力3.1-1.44.24.11.6-3.62.81.5 TFP增长贡献率37.936.551.924.146.077.735.445.7中技术全要素生产率7.28.38.45.02.55.40.31.9 制造业技术进步8.18.38.47.54.68.62.62.6 技术效率-0.80.00.0-2.3-2.0-3.0-2.3-0.7 实际销售产值12.10.916.712.09.51.712.28.6 实际资本存量12.1-4.713.413.98.0-5.617.38.6 劳动力1.7-5.34.92.12.4-2.64.41.3 TFP增长贡献率59.5922.250.341.726.3317.62.522.1高技术全要素生产率4.45.43.94.04.15.54.32.4 制造业技术进步3.55.24.60.93.65.73.21.9 技术效率0.80.1-0.73.00.4-0.21.00.5 实际销售产值13.09.012.318.713.27.916.311.0 实际资本存量11.45.011.216.810.13.013.48.8 劳动力3.81.23.75.44.41.16.62.5 TFP增长贡献率33.860.031.721.431.169.626.421.8

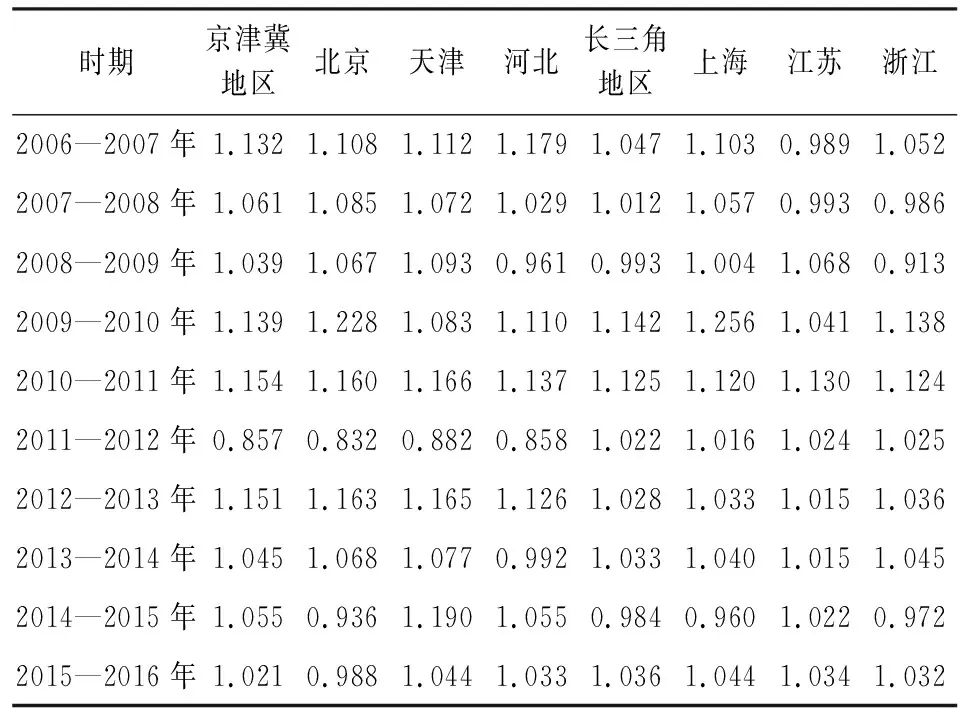
表2 2006—2016年期间历年制造业全要素生产率指数

五、京津冀和长三角地区全要素生产率的比较

(一)整体比较

2006—2016年期间，京津冀地区制造业全要素生产率年均增长率及全要素生产率的增长贡献率皆高于长三角地区，京津冀地区制造业全要素生产率年均增长6.2%，增长贡献率达46.3%；而长三角地区制造业全要素生产率年均增长为4.1%，增长贡献率为33.1%。从六省市情况来看，天津制造业的全要素生产率增长最快，上海、北京、河北、江苏依次随后，浙江最慢。仅有天津和上海的制造业全要素生产率的增速高于所在地区的整体水平，表明天津和上海分别是京津冀地区和长三角地区制造业全要素生产率增长的主动力。但是，就增长贡献率而言，上海、北京和天津位居前三位，江苏、浙江和河北位居后三位。上海和北京的增长贡献率皆高于70%，表明其制造业的增长主要靠要素投入之外的技术进步和能力实现，属于效率型增长；江苏、浙江和河北的增长贡献率皆不足30%，表明其制造业的增长主要依赖资本、劳动力等要素投入，属于投入型增长；天津的增长贡献率为55.6%，介于两者之间，表明其制造业的增长由要素投入及其以外的因素共同驱动。就技术进步变化情况而言，京津冀地区制造业的前沿生产面“向外”扩张的程度较长三角地区更为明显，在六省市中，上海技术进步年均增长率最高，达5.3%；浙江技术进步年均增长率最低，为2.0%。两大区域及六省市制造业的技术效率年均增长率皆为正值，表明其利用技术的能力皆有所提升。

(二)分行业比较

在低技术、中技术和高技术制造业三大领域，京津冀地区全要素生产率的增长表现皆优于长三角地区，且在中技术制造业领域的领先优势最为明显，较后者年均增速高出4.7个百分点。低技术制造业领域，天津的全要素生产率年均增速最高，北京最低；中技术制造业领域，天津的全要素生产率年均增速最高，江苏最低；高技术制造业领域，上海的全要素生产率年均增速最高，浙江最低。值得注意的是，尽管北京和上海在中技术制造业领域的全要素生产率并非最高，但其全要素生产率增长贡献率分别高达922.2%和317.6%，这是由于北京、上海两地中技术制造业的资本和人力两大要素投入均呈负增长，但产出呈小幅增长态势，表明全要素生产率已是该行业增长绝对主导性的驱动力量。

根据六省市在制造业三大类别中的表现，可以发现制约北京制造业全要素生产率增长的短板主要是低技术制造业领域，该领域全要素增长率年均增速不仅在六省市中位居末位，而且比自身中技术制造业和高技术制造业领域分别低1.9和4.8个百分点；制约天津制造业全要素生产率增长的短板主要是高技术制造业领域，该领域全要素增长率年均增速不仅在六省市中位列第五，而且比自身低技术制造业和中技术制造业领域分别低9.5和4.5个百分点；制约江苏制造业全要素生产率增长的短板主要是中技术制造业领域，该领域全要素增长率年均增速不仅在六省市中位居末位，而且比自身低技术制造业和高技术制造业领域分别低4.9和4.0个百分点；制约浙江制造业全要素生产率增长的短板主要是中技术和高技术制造业领域，该领域全要素增长率年均增速不仅在六省市中分别位居第五和第六，而且比自身低技术制造业领域分别低2.9和2.4个百分点；上海和河北在低技术制造业、中技术制造业和高技术制造业三大类别中的全要素生产率增长表现相对均衡，上海表现更佳，不仅增长表现相对均衡，而且在三大类别领域皆保持较高的年均增长速度。

(三)分时期比较

京津冀地区、长三角地区及六省市在2006—2016年间仅在少数年度的全要素生产率增长率为负，计算后发现，虽然京津冀地区制造业全要素生产率年均增长率高于长三角地区，但是波动程度同样高于后者。

京津冀地区制造业全要素生产率在2011—2012年期间出现明显下滑，当年增长率为-14.3%。分析原因，从地域因素看，北京、天津、河北三省市同期制造业全要素生产率分别下滑16.8%、11.8%和14.2%；从领域类别看，主要是低技术制造业全要素生产率同期大幅下滑37.5%。根据当期投入产出数据，2011—2012年期间，京津冀地区制造业实际销售产值增长率虽然高达54.0%，劳动力投入增长率为20.0%，但实际资本存量增长率高达148.2%，表明产出的增长过于依赖资本的投入，这可能是当期全要素生产率下滑的直接原因。

长三角地区制造业全要素生产率仅在2008—2009年和2014—2015年期间分别小幅下滑0.7%和1.6%。分析发现，2008—2009年负增长主要原因是浙江制造业尤其是中技术制造业全要素生产率的下滑(增长率分别为-1.4%和-5.2%)，而2014—2015年负增长主要是因为上海、浙江制造业尤其是中技术制造业全要素生产率的下滑(上海制造业和中技术制造业增长率分别为-4.0%和-9.7%；浙江制造业和中技术制造业增长率分别为-2.8%和-6.4%)。根据当期投入产出数据，2008—2009年期间，浙江中技术制造业实际销售产值下降-1.3%，虽然劳动力投入也下降5.7%，但实际资本存量增长率高达21.7%，表明其产出的增长过于依赖资本的投入；2014—2015年期间，上海和浙江中技术制造业实际资本存量增长率皆为正值，但实际销售产值下降的速度明显超过劳动力投入下降的速度，表明上海和浙江全要素生产率的下滑对制造业产出下降的影响较要素投入的减少尤其是劳动力投入的减少更为明显。

六、结论与启示

(一)研究结论

通过前述分析，可以得出以下几点结论。第一，京津冀地区在低技术制造业、中技术制造业和高技术制造业三个类别领域的全要素生产率年均增长率皆高于长三角地区，但其制造业全要素生产率整体波动变化情况也较长三角地区更为明显。第二，京津冀地区制造业技术进步增长率、技术效率增长率以及全要素生产率对制造业产出增长的贡献率皆高于长三角地区。第三，六省市中天津制造业全要素生产率的增长率最高，浙江最低，且京津冀地区和长三角地区中分别仅有天津和上海制造业全要素生产率的增长率高于所在地区整体水平，但就增长贡献率来看只有上海和北京的制造业属于效率型增长，江苏、浙江和河北仍然属于投入型增长，天津则介于两者之间。第四，上海在不同制造业类别中的全要素生产率的增长呈较高水平的均衡，河北则保持较低水平的均衡，而制约北京制造业全要素生产率增长的短板主要是低技术制造业领域，制约天津制造业全要素生产率增长的短板主要是高技术制造业领域，制约江苏制造业全要素生产率增长的短板主要是中技术制造业领域，浙江则在中技术制造业和高技术制造业领域皆存在较为明显的短板。

(二)政策启示

尽管上海和北京制造业全要素生产率整体具有较高的增长贡献率，属于效率型增长，但包括其在内的京津冀地区和长三角地区各省市，在2006—2016年期间皆有全要素生产率下滑的年份，而且此时通常是制造业实际资本增长率大幅高于实际产出增长率，反映全要素生产率下滑的时期制造业产出增长对资本的依赖度较高而利用率较低，因此六省市皆应在持续优化全要素生产率提升体制环境的同时，着力优化投资结构，改善制造业对资本投入的整体利用效率，从而改变产出增长过于依赖资本投入的弊端，实现生产要素向效率更高的产业、行业和企业集中[16]。

对于京津冀三省市而言，低技术制造业是制约北京制造业全要素生产率进一步增长的短板所在，尽管北京低技术制造业的劳动力投入已逐步下降，但资本投入仍呈扩张态势，因此北京应重点改善低技术制造业的资本使用效率。高技术制造业是制约天津制造业全要素生产率增长的短板所在，鉴于天津高技术制造业要素投入呈扩张态势且资本要素投入扩张更为明显，天津应调整优化高技术制造业资本、劳动力等要素投入的比例关系，重点改善高技术制造业的要素使用效率尤其是资本利用效率。河北三大类别制造业全要素生产率的增长速度在六省市中皆处中游位置，针对其各类别制造业的资本、劳动力等要素投入规模皆呈明显扩张的态势，河北应在改善制造业的资本使用效率的同时，加强人力资本积累，着力提升劳动者素质。

对于长三角三省市而言，上海低技术制造业和中技术制造业的全要素生产率还有进一步提升的空间，针对其中技术制造业要素投入规模呈收缩而低技术制造业资本要素投入仍呈扩张的态势，上海应优先改善低技术制造业的资本利用效率。中技术制造业是制约江苏制造业全要素生产率增长的短板所在，鉴于其中技术制造业要素投入呈扩张且资本要素投入扩张更为明显，江苏需尽快改善中技术制造业的要素使用效率尤其是资本利用效率。浙江不仅技术进步年均增速在六省市中最低，而且低技术和中技术制造业皆是制约其制造业全要素生产率增长的短板，鉴于其低技术和中技术制造业要素投入皆呈扩张且资本要素投入扩张更为明显，浙江应在大力改善低技术和中技术制造业的要素使用效率尤其是资本利用效率的同时，不断加大创新投入力度，夯实全要素生产率提升的科技基础。