偶合KdV方程的行波解分支

2019-07-25全寿湘赵海霞唐生强

桂林电子科技大学学报 2019年2期

关键词：波解轨线偶合

全寿湘，赵海霞，唐生强

(1.桂林电子科技大学数学与计算科学学院，广西桂林 541004；2.桂林电子科技大学广西密码学与信息安全重点实验室，广西桂林 541004)

在非线性波研究中，偶合KdV方程为[1]：

qt+aqnqx+brmrx+βqxxx=0；

(1)

rt+kqlrx+αrxxx=0。

(2)

其中，q=q(x,t),r=r(x,t)，a、b、α、β、k为非零常数，l、m、n为正整数。偶合KdV方程是描述双层浅水波动力学的主要模型，能解释诸如漏油事件引起的双层流体的物理现象。Krishnan等[1]用图方法推导了偶合KdV方程解的结构，讨论了在非线性幂律的情形下，当方程仅有1个或2个非线性幂律参数支持拓扑孤子解或激波解时，该方程有拓扑孤子解，并用乘方法推出守恒定律，以此求出偶合KdV方程的守恒量，但其并未研究该方程的行波解的动力系统分支性态。为此，研究l=m=n条件下偶合KdV方程行波解的动力系统分支性态，并给出在这个系统的参数空间的所有行波解。

1 偶合KdV方程的动力系统

令r(x,t)=σq(x,t),σ≠0，l=m=n，则式(1)、(2)可化为：

(3)

(4)

(5)

(6)

(7)

显然，式(7)是一个Hamilton系统，它的首次积分为

(8)

系统(7)是一个五参数空间(k，n，α，c，g)的平面自治动力系统，对一个固定的α和不同的n、k，研究当参数c、g变化时，在相平面(φ,y)内系统(7)的相图的分支。由于所考虑的物理模型对有界行波解才有意义，仅关注系统(7)的有界解。

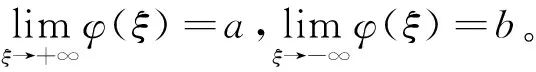
2 系统(7)的相图分支

只讨论α>0，k>0时的情形，若α<0或k<0，则可作α→-α，k→-k，c→-c，g→-g变换，将其转化为原系统。记

有

当f(φ0)<0时，系统(7)无奇点；当f(φ0)>0，c>0，f(0)=g>0或g<0时，系统(7)存在2个奇点：Si(φi,0),i=1,2,φ1<0<φ2或0<φ1<φ2；当f(φ0)>0，c<0，f(0)=g>0或g<0时，系统(7)存在2个奇点：Si(φi,0),i=1,2,φ1<0<φ2或φ1<φ2<0。

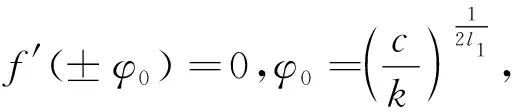
在(c，g)参数平面分别隐含下述关系：

假设M(φi，yi)是系统(7)的线性化系统在奇点(φi，yi)的系数矩阵，则有

由平面动力系统理论可知，对一个平面自治可积系统的奇点：若J<0，则奇点是一个鞍点；若J>0，且tr(M(φi,yi))=0，则奇点是一个中心点；若J>0，且(tr(M(φi,yi)))2-4J(φi,yi)=0，则奇点是一个结点；若J=0，且奇点的指标为0，则奇点是一个高阶奇点。

对式(8)所定义的函数H(φ,y)，记

在(c，g)参数平面，系统(7)的相图分支曲线Li,i=1,2,3，直线g=0和c=0将参数空间划分成若干个区域，如图1所示。

图1 k>0时，系统(7)在(c,g)参数平面内的分支曲线

当n=2l1-1时，A2区域无奇点，系统(7)相图

如图2所示。

当n=2l1时，B1与B4、B2与B3、B5与B6区域的相图分别关于y轴对称，如图3所示。

3 当n=1，n=2，g≠0时，方程(5)的显式精确行波解

3.1 n=1时方程(5)的显式精确行波解

当n=1时，对系统(7)，分支曲线如图1(a)所示。

图2 n=2l1-1时系统(7)的相图

当(c,g)∈A1时，由式(8)所定义的轨线H(φ,y)=h,h∈(h2,h1)有代数方程：

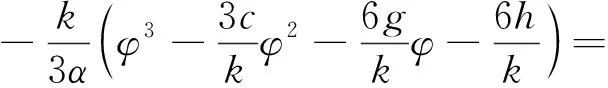
(9)

由式(9)可得，

解之得周期波解：

当(c,g)∈A1时，由式(8)所定义的轨线H(φ,y)=h1为系统(7)过奇点(φ1,0)的同宿轨，其代数方程为

(10)

由式(10)可得,

解之得孤立波解：

3.2 n=2时方程(5)的显式精确行波解

当n=2时，对系统(7)，分支曲线如图1(b)所示。图3中B1与B4、B2与B3、B5与B6的相图分别关于y轴对称，因此只讨论(c,g)∈B1，(c,g)∈B2，(c,g)∈B5的精确解。

当(c,g)∈B1，由式(8)所定义的轨线H(φ,y)=h,h∈(h1,+∞)有代数方程：

(11)

由式(11)可得

解之得周期波解：

φ(ξ)=

其中，

当(c,g)∈B2，由式(8)所定义的轨线H(φ,y)=h，h∈(h1，h3]及h∈(h2,+∞)的代数方程形同式(11)，故其解的情形与(c,g)∈B1相似，此处不再赘述。由式(8)所定义的轨线H(φ,y)=h，h∈(h3,h2)有代数方程：

φD<φE<φF<φG。

(12)

由式(12)可得，

解之得周期波解：

φ(ξ)=

其中，

由式(8)所定义的轨线H(φ,y)=h2为系统(7)过奇点(φ2,0)的同宿轨，其代数方程为：

(13)

由式(13)可得，

解之得孤立波解：

φ(ξ)=

当(c,g)∈B5，由式(8)所定义的轨线H(φ,y)=h，h∈(h1，+∞)的代数方程形同式(11)，故其解的情形与(c,g)∈B1相似，此处不再赘述。

4 g=0时方程(5)的显式精确行波解

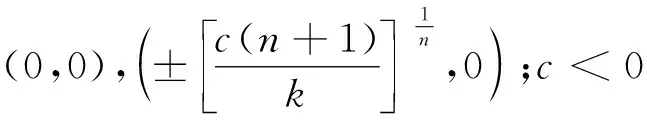
4.1 方程(5)的孤立波解

当c>0时，由式(8)所定义的轨线H(φ,y)=0为系统(7)过奇点(0,0)的同宿轨(图2(b)，图3(g))，其代数方程为

(14)

由式(14)可得，

解之可得

当n=2l1时，

当n=2l1-1时，

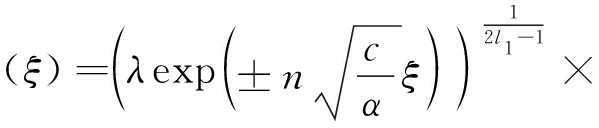
当c<0，n=1时，由(8)所定义的轨线H(φ,y)=h1为系统(7)过奇点(φ1,0)的同宿轨(图2(c))，φ1=2c/k，其代数方程为

(15)

由式(15)可得

解之得孤立波解：

4.2 方程(5)的周期波解

当n=1时，由式(8)所定义的H(φ,y)=h，h∈(h2,h1)(图2(b)、(c))的代数方程形同方程(9)，故其解与之相似，此处不再赘述。

当n=2,c>0时(图3(g))，由式(8)所定义的H(φ,y)=h，h∈(h1,0)有代数方程：

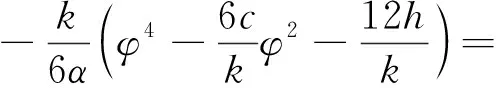
0<φM<φN。

(16)

由式(16)可得

解之得周期波解：

φ(ξ)=

由式(8)所定义的H(φ,y)=h，h∈(0,+∞)有代数方程：

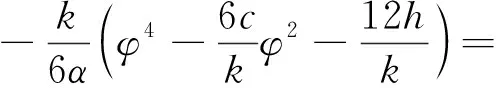
(17)

由式(17)可得，

解之得周期波解：

当n=2,c<0(图3(h))，由式(8)所定义的H(φ,y)=h，h∈(0,+∞)的代数方程形同方程(17)，故其解的情形与之相似，此处不再赘述。

5 方程(4)的光滑孤立波解和无穷多光滑周期波解

2)若n=2l1-1，g=0，则相对于由(7)所定义的曲线H(φ,y)=h1的分支，方程(4)有1个光滑峰形孤立波解；相对于由系统(7)所定义的曲线H(φ，y)=h，h∈(h2,h1)的分支，方程(4)有一族光滑周期波解(见图2(b)、(c))。

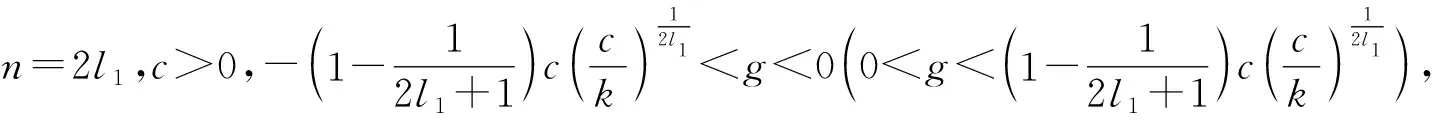
3)若n=2l1，c>0，g=0，则相对于由系统(7)所定义的曲线H(φ,y)=0的分支，方程(4)有2个光滑孤立波解，分别为谷形光滑孤立波解和峰形光滑孤立波解；相对于由系统(7)所定义的曲线H(φ，y)=h，h∈(h1,0)及h∈(0,+∞)的分支，方程(4)有2族光滑周期波解(见图(3(g)))。

4)若n=2l1，c<0，则相对于由系统(7)所定义的曲线H(φ，y)=h，h∈(h1,+∞)的分支，方程(4)有1族光滑周期波解(见图3(e)、(f)、(h))。

一般地，在g≠0，h≠0情况下，使用首次积分式(8)和系统(7)的第一个方程，不可能得到方程(4)的用参数表示的显式精确行波解。