基于多项式预处理的特殊双变量矩阵方程异类约束解算法
2019-07-25周咸富段复建
周咸富,段复建
(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)
讨论一类特殊的双变量矩阵方程
AXB+AYB=F
(1)
的异类约束解加速问题,其中A,B,F∈Rn×n,X∈Rn×n,Y∈SRn×n,且A、B是对称正定矩阵。对于方程(1)的研究,不同约束条件可用不同的方法,一般采用共轭梯度法求解。刘莉[1]利用共轭梯度法求矩阵方程AXB+CYD=E的中心对称最小二乘解;方玲等[2]利用极小残差法求解AXB+CYD=E的对称最小二乘解。但这些方法迭代过程中的收敛性不确定,即便收敛,收敛速度也较慢。针对收敛速度慢的问题,进行预处理是提高收敛速度的主要途径之一。Zhao等[3]提出了一种基于参数迭代预处理方法和共轭梯度修正形式(MCG)相结合的并行预条件求解算法;温瑞萍等[4]提出了不完全SAOR预条件共轭梯度法;Jia等[5]提出了一种基于残差的稀疏近似反预处理方法。对于矩阵方程异类约束解问题,李书连等[6]通过修改系数矩阵和其方向,提出了修正共轭梯度算法,解决了双变量矩阵方程组最小二乘问题;牛婷婷等[7]将多变量异类约束问题推广到一类离散时间代数Riccati矩阵方程,建立了双迭代算法;宋卫红等[8]利用逆矩阵的Neumann级数形式,将多变量异类约束解推广到离散对偶代数Riccati矩阵方程,构造了双迭代算法。
预处理方法大多应用于解同类线性方程组,用于双变量矩阵方程异类约束条件的研究不多,且对于异类约束的矩阵方程收敛速度的研究也不多见。因此,将多项式预处理[9]和共轭梯度法相结合,提出多项式预处理共轭梯度法。
1 多项式预处理技术
定义同阶对称正定矩阵A与B的內积为[A,B]=tr(ATB),由此导出的Frobenius范数为
设Rn×n为n×n阶矩阵集合,SRn×n为n×n阶对称矩阵集合,σ为A的任意奇异值,S=[a,b]为σ的取值区间,a和b分别为σ的最小与最大奇异值,τ为B的任意奇异值,L=[d,e]为τ的取值区间,d和e分别为λ的最小、最大奇异值。
迭代法求解矩阵方程,收敛速度与系数矩阵奇异值的分布有关。奇异值分布越集中,条件数越接近于1,收敛速度越快,反之,则会很慢。利用多项式对矩阵方程进行预处理,可使其奇异值的分布相对集中,条件数接近于1,从而提高收敛速度。
对矩阵方程AXB+AYB=F作等价变换
C(A)AXBC(B)+C(A)AYBC(B)=C(A)FC(B),
(2)
其中C(A)、C(B)为次数小于n的实系数多项式矩阵。若C(A)A和C(B)B的谱条件远远小于A、B的谱条件数,则利用共轭梯度法求解式(2)的收敛速度将大大快于直接求式(1)的收敛速度。所以选取系数多项式时,应使C(A)和C(B)在某种意义下接近A-1和B-1,这样经过处理后的迭代次数远比之前少。若A或B的最大奇异值和最小奇异值相差不大,则不需要进行预处理。令
F(A)=C(A)A,G(B)=BC(B),
Q=C(A)FC(B),
则式(1)的求解问题等价于
F(A)XG(B)+F(A)YG(B)=Q
(3)
的求解。
由多项式插值原理可得A的预处理多项式:
(4)
(5)
(6)

a≤σi≤b,i=1,2,…,n,
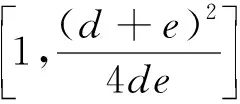
d≤τi≤e,i=1,2,…,n,
定义1设A∈Rn×n,A为非奇异矩阵,‖·‖为定义在Rn×n上的范数矩阵,称
cond(A)v=‖A-1‖v‖A‖v,v=1,2,or,∞
为A关于范数‖·‖的条件数。
通常情况下,若矩阵A的条件数大,则称A为病态矩阵,反之称为良态矩阵,条件数越趋近于1,则越稳定。
采用最常见的Frobenius范数反映矩阵病态性,
当A为实对称矩阵时,有
其中λmax、λmin分别为矩阵A最大、最小特征值。
定理1设式(1)中系数的谱条件数较大,经过一次多项式预处理后,得到新的矩阵方程最小与最大奇异值比值比原方程最小与最大奇异值比值提高16倍。
证明设经过一次插值多项式预条件,得到C(A)A的最小、最大特征值分别为a′、b′,C(B)B的最小、最大特征值分别为d′、e′。记

2 多项式预处理共轭梯度算法
对于方程(1)用共轭梯度法求解,若条件数远大于1,则收敛速度较慢。为了提高收敛速度,引入多项式预处理技术构造新的算法。
算法1定义1+ε1,1+ε2,(ε1>0,ε2>0)分别为系数矩阵A、B的非零最大、最小奇异值比值的满意的临界值。
1)给出初始解X0∈Rn×n、Y0∈SRn×n和初始边界a0、b0、d0、e0。
2)对于i=0,1,…,n,求矩阵多项式:
3)若bi/ai≤1+ε,ei/di≤1+ε2,则停止预处理,转步骤5),否则,令
Ai+1=F(Ai),
Bi+1=G(Bi),
Qi+1=C(Ai)FC(Bi)。
4)计算ai+1=1,bi+1=(ai+bi)2/4aibi,di+1=1,ei+1=(di+ei)2/4diei,转步骤2),i=i+1。
5)令
F(A)=F(Ai),G(B)=G(Bi),Q=Qi+1。
6)计算
R0=Q-(F(A)X0G(B)+F(A)Y0G(B)),
P0=FT(A)R0GT(B),
U0=P0,
V0=Q0,k=0。
7)若Rk=0,或Rk≠0,而‖Uk‖2+‖Vk‖2=0,停止,否则,k=k+1。
8)计算
Xk=Xk-1+αk-1Uk-1,
Yk=Yk-1+αk-1Vk-1,
Rk=Q-(F(A)XkG(B)+F(A)YkG(B))。
9)计算

10)转步骤8)。
需要注意的是,在实际求解中,系数矩阵的最大与最小奇异值很难求出,因此,利用上述算法在求解C(A)、C(B)时,对于a0、b0、d0、e0可利用合适的估计式,
对于算法1,一般都有以下2个性质。
性质1若矩阵方程(3)是相容的,算法中{Ri}、{Ui}、{Vi}满足以下关系:
〈Ri,Rj〉=0, 〈Ui,Uj〉+〈Vi,Vj〉=0,
其中i,j=1,2,…,k,i≠j。
性质2若线性方程(1)是相容的,且[X*,Y*]是其一个解,则对于任意初始矩阵对[X0,Y0],算法中的迭代序列{Xi}、{Yi}、{Ri}、{Pi}、{Qi}、{Ui}、{Vi}满足如下关系:
其中i=1,2,…,k-1。
定理2若矩阵方程(1)有解,则对任意选定的初始迭代矩阵对[X1,Y1],应用算法1,矩阵方程(1)异类约束解可经过有限步迭代得到。
证明若Ri≠0,i=1,2,…,pq,由性质2可得‖Ui‖2+‖Vi‖2≠0。根据算法1,由迭代计算可得Rpq+1、Upq+1、Vpq+1,且由性质1知
〈Rpq+1,Ri〉=0, 〈Ri,Rj〉=0,
其中i,j=1,2,…,pq,i≠j。序列{Ri}构成了矩阵空间Rp×q的一个正交基,故Rpq+1=0,即Xpq+1、Ypq+1为方程的一个解。
引理1设算法产生的迭代序列{Xk}在某种范数意义下收敛,
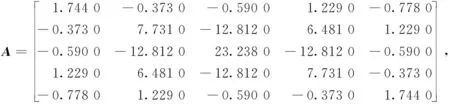
若存在实数α>0和一个与迭代次数无关的常数0 ‖Xk+1-X*‖=q‖Xk-X*‖α, 则称算法产生的迭代序列{Xk}具有Q-α阶收敛速度。特别地,当α=1,0 为证明多项式预处理共轭梯度法产生的迭代序列{Xk}、{Yk}具有Q-线性收敛速度,作如下变换。 记Mk=Xk-X*,Nk=Yk-Y*,则Mk+1=Mk+αkUk,Nk+1=Nk+αkVk,即 且由性质2可知,对任意的i≠k,有 (7) (8) 结合算法1,经过计算证明,产生的序列{Mk}、{Nk}具有如下结论。 性质3对k≥1,有 (9) (10) 证明由式(7)、(8)可得 tr((Mk+αkUk)T(Mk+αkUk))+ tr((Nk+αkVk)T(Nk+αkVk))= 2αk‖Rk‖2=‖Mk‖2+‖Nk‖2+ (‖Uk‖2+‖Vk‖2)= 定理3设迭代序列{Xk}、{Yk}由多项式预处理共轭梯度算法经过0次预处理产生,且A、B为对称正定矩阵,则有 (11) 其中X*、Y*是方程(1)的解,σn=a,σ1=b,τq=d,τ1=e分别是A、B的最小、最大奇异值。 证明假定A、B的奇异值分解为 A=UΣVT,B=WDTT。 (12) 其中:U、V、W、T皆为正交矩阵; 且 b=σ1≥σ2≥…≥σn=a, e=τ1≥τ2≥…≥τq=d。 由式(10)、(12)可得, ‖Mk+1‖2+‖Nk+1‖2+ ‖Mk+1‖2+‖Nk+1‖2+ ‖Mk+1‖2+‖Nk+1‖2+ ‖Mk+1‖2+‖Nk+1‖2+ ‖Mk+1‖2+‖Nk+1‖2+ ‖Mk+1‖2+‖Nk+1‖2+ ‖Mk+1‖2+‖Nk+1‖2≤ 即有 定理4多项式预处理共轭梯度算法经过一次预处理后的Q-收敛速度为 证明由定理1知,经过一次预处理,最小与最大奇异值比值提高了16倍,结合定理3可得结论,证毕。 已知矩阵A,B,F∈R5×5,且A、B是对称正定矩阵,求X∈R5×5,Y∈SR5×5,使 AXB+AYB=F。 X0=zeros(5), Y0=zeros(5)。 其中A的最大和最小奇异值分别为b=37.436 0,a=0.024 0,B的最大和最小奇异值分别为e=97.310 1,d=0.025 1。 使用共轭梯度迭代法进行求解,在迭代过程中,取ε=1×10-8作为迭代终止条件,即当‖Rk‖<ε,迭代停止。对于本例,可以求得如下结果: 迭代次数k=3 510,迭代时间t=0.287 921 s,误差‖R3 510‖=6.637 3×10-9<ε。 利用多项式预处理共轭梯度算法,求解AXB+AYB=F。同样的迭代终止条件,本算法的迭代结果如表1所示。从表1可看出,预处理次数i=10,迭代次数k=12,迭代时间t=0.005 191 s,本算法比共轭梯度法迭代次数减少了3 498,迭代时间缩短了0.282 730 s。 表1 本算法的迭代结果 基于共轭梯度算法,引入多项式预处理技术,构造了多项式预处理共轭梯度算法,并用于求解特殊双变量矩阵方程异类约束的问题,同时证明了该算法是收敛,且具有Q-线性收敛速度。数值实验表明,多项式预处理共轭梯度算法比共轭梯度算法收敛速度更快,需要的迭代时间更短,且算法是有效、可行的。


3 数值实验





4 结束语
