运用SPSS软件对试验数据回归建模开发高强高导热压铸铝合金材料

陈苏坚

广州致远新材料科技有限公司，广东 广州 511470

在开发具有特定性能的铝合金材料的过程中，需要通过大量的试验数据进行定性和定量的分析，以找出其规律性或趋势性．尤其是在多种元素成分的组合对性能的影响中，既有单个元素的影响，又存在各元素之间交互作用的影响．SPSS是一款很好的可用于回归分析的软件[1-2]，用此软件，基于试验数据基础上的回归分析、拟合建模，对于开发特定性能的铝合金材料，可以起到很好的辅助设计作用．

为研制一种高强高导热压铸铝合金材料，运用SPSS软件对23组铝合金材料的试验数据进行线性回归分析，建立数学模型，并通过多个模型的组合制定出待开发的铝合金材料的主要成分和变质方案．

1 试验基础数据

表1为23组铝合金材料的试验数据．在建模和分析中，将表1试验数据中的主要成分和变质材料加入量作为自变量，5项性能分别作为5个不同的对应因变量，进行多元线性回归建模．

2 SPSS线性回归建模的主要分析参数及其运行选项的设定

2.1 线性回归建模的主要分析参数

根据试验数据进行回归建模，分析参数主要有以下3个．R2(复相关系数)是判定线性方程拟合优度的重要指标，为提高准确度分析时采用软件运算的调整R2．当拟合优度达到0.1(R2=0.01)时为小效应，0.3(R2=0.09)时为中等效应，0.5(R2=0.25)时为大效应．当Sig(回归系数显著性值)小于0.05时，表明建立的线性关系回归系数存在，模型具有显著(若等于0.000则具有极显著)的统计学意义．VIF(多重共线性检验值)反映自变量之间存在某种函数关系.此时无法做到固定其他条件单独考查一个自变量的作用，所观察的这个自变量效应总是混杂了其他自变量的作用，使得对自变量效应的分析不准确而造成分析误差，所以在分析铝合金材料成分之间有没有存在明显的交互作用，需要进行多重共线性的判断和排除多重共线性的影响．VIF值越大，显示共线性越严重．一般判断：当VIF<10时，不存在多重共线性；当10≤VIF<100时，出现较强的多重共线性；当VIF≥100时，存在严重多重共线性．

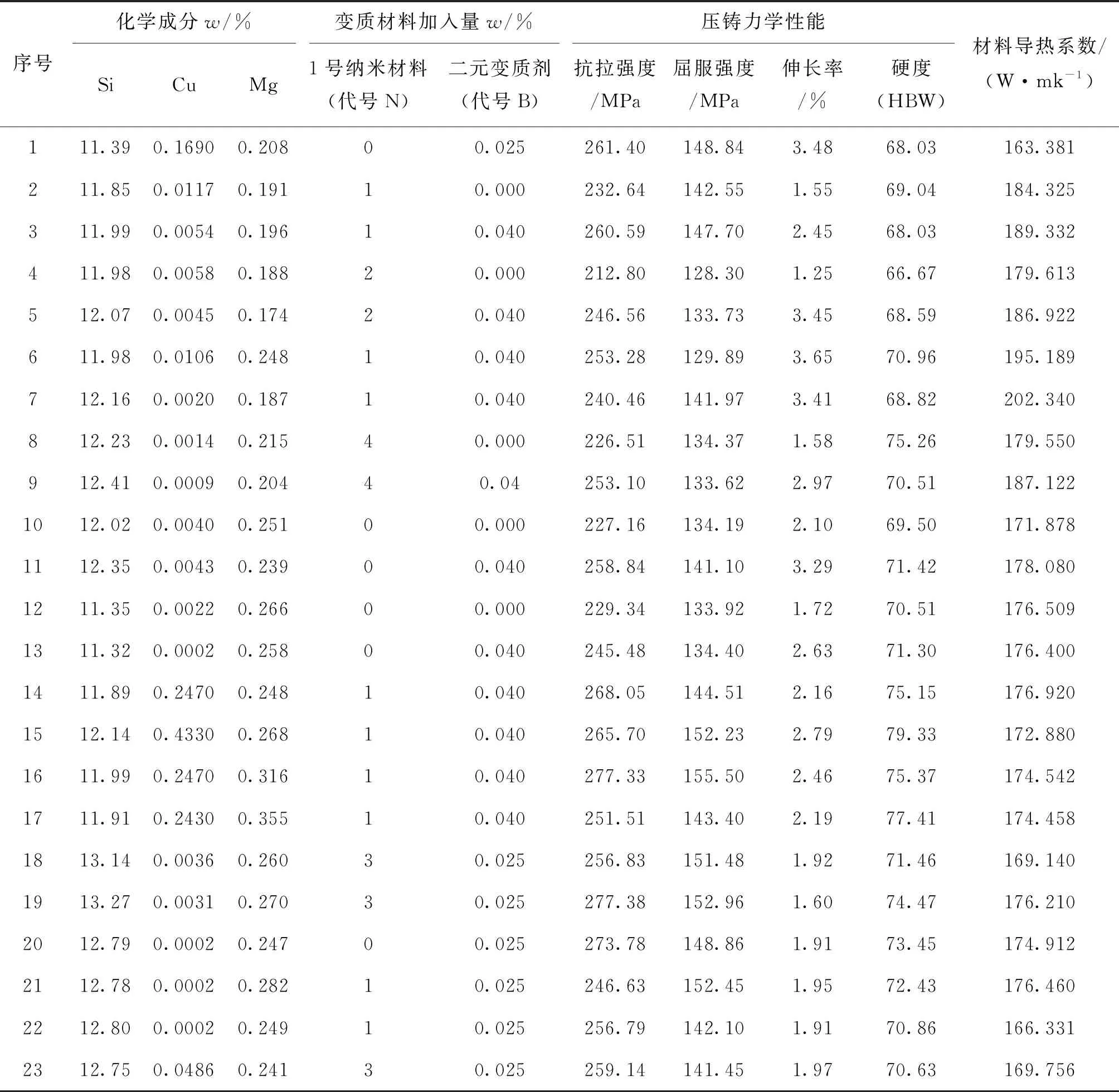
表1 试验基础数据

2.2 运行选项的设定

根据所需分析的主要参数，在运行SPSS中设定了以下相应的选项：每次拟合的自变量5个，对应因变量一个；在线性回归方法中，选择“逐步”法，以便使拟合的模型对比“输入”法更能反映客观性；在线性回归统计中，选择“模型拟合度”和“共线性诊断”，回归系数勾选“估计”项，其它选项均按默认．

3 建模及其分析

3.1 抗拉强度作为因变量建模

按照设定选项运行SPSS，抗拉强度的建模数据详见表2．从表2可见，软件运行后给出了三个模型，为提高模型的拟合优度，选择模型3．模型3的调整后R2达到了0.605，标准估计误差为最小，表明模型3的拟合优度较好，达到了大效应．从表2数据可得出，二元变质剂、Si和Cu的显著性指标Sig均小于0.05，表明这三个自变量对因变量抗拉强度所产生的影响具有显著性，所建立的线性关系回归系数存在且回归模型较好，回归方程具有统计学意义．二元变质剂、Si和Cu三个自变量多重共线性检验指标VIF的值都远低于10，表明这三个自变量之间不存在多重共线性，它们之间的作用程度不影响各自效应分析的准确性．

通过数据分析，拟合的模型能有效反映出这三个自变量对因变量抗拉强度的因果关系影响的客观性．抗拉强度模型的方程为：YK=65.467+13.72Si+46.538Cu+583.689B.

3.2 屈服强度作为因变量建模

按照设定选项运行SPSS，屈服强度的建模数据详见表3．

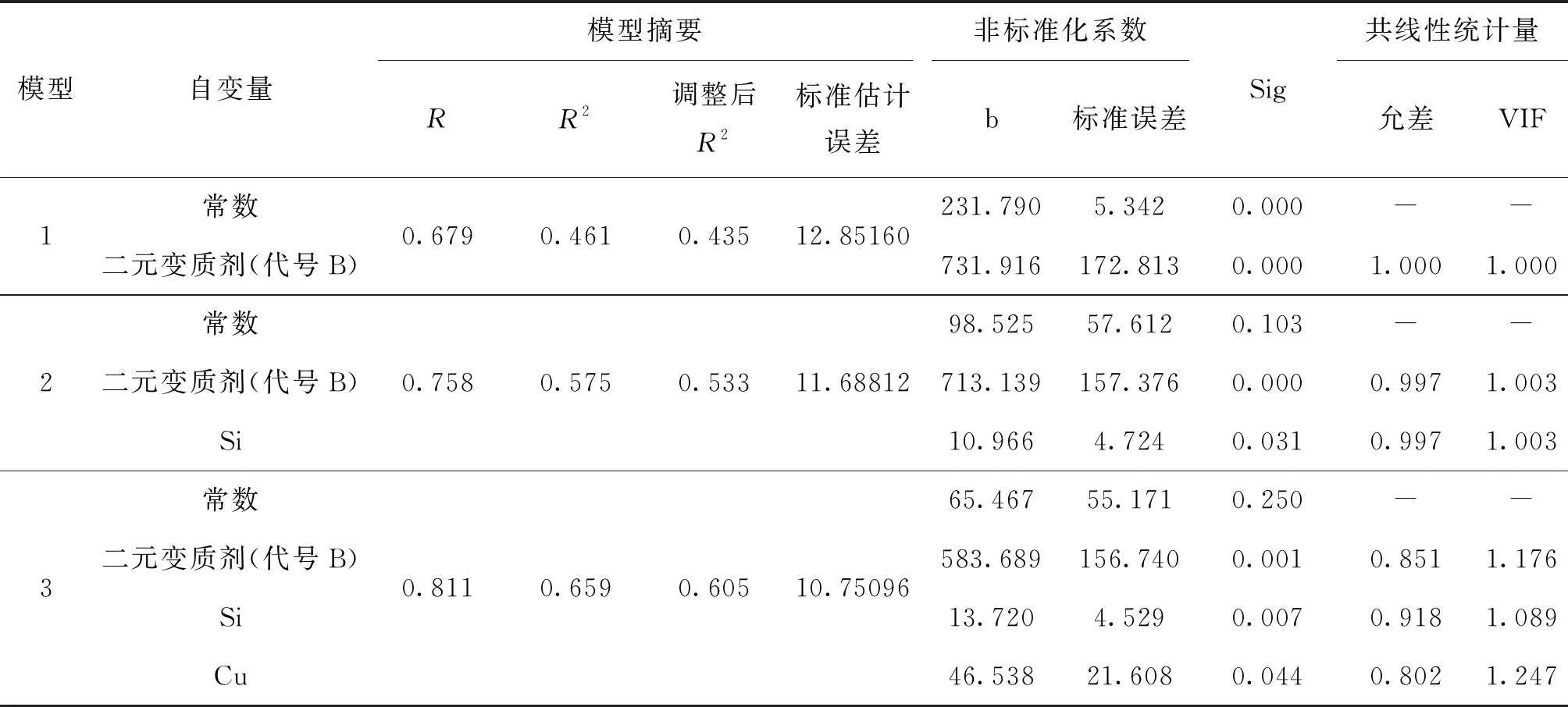
表2 抗拉强度建模数据

从表3可见，软件运行后给出了三个模型，为提高模型的拟合优度，选择模型3．模型3的调整后R2达到了0.516，标准估计误差为最小，表明模型3的拟合优度很好，达到了大效应．从表3数据可得出， Cu和Si及1号纳米材料的显著性指标Sig均小于0.05，表明这三个自变量对因变量屈服强度所产生的影响具有显著性，所建立的线性关系回归系数存在且回归模型较好，回归方程具有统计学意义． Cu和Si及1号纳米材料三个自变量多重共线性检验指标VIF的值都远低于10，表明这三个自变量之间不存在多重共线性，它们之间的作用程度不影响各自效应分析的准确性．

通过数据分析，拟合的模型能有效反映出这三个自变量对因变量屈服强度的因果关系影响的客观性．屈服强度模型的方程为：YQ=5.102+11.299Si+38.563Cu-2.382N.

3.3 伸长率作为因变量建模

按照设定选项运行SPSS，伸长率的建模数据详见表4．

从表4可见，软件运行后给出了三个模型，为提高模型的拟合优度，选择模型3．模型3的调整后R2达到了0.627，标准估计误差为最小，表明模型3的拟合优度较好，达到了大效应．从表4数据可得出，二元变质剂的显著性指标Sig值为0.000，表明它对因变量伸长率产生的影响具有极显著性，Mg和Si的显著性指标Sig均小于0.05，表明这两个自变量对因变量伸长率所产生的影响具有显著性，它们所建立的线性关系回归系数存在且回归模型较好，回归方程具有统计学意义．二元变质剂、Mg及Si三个自变量多重共线性检验指标VIF的值都远低于10，表明这三个自变量之间不存在多重共线性，它们之间的作用程度不影响各自效应分析的准确性．

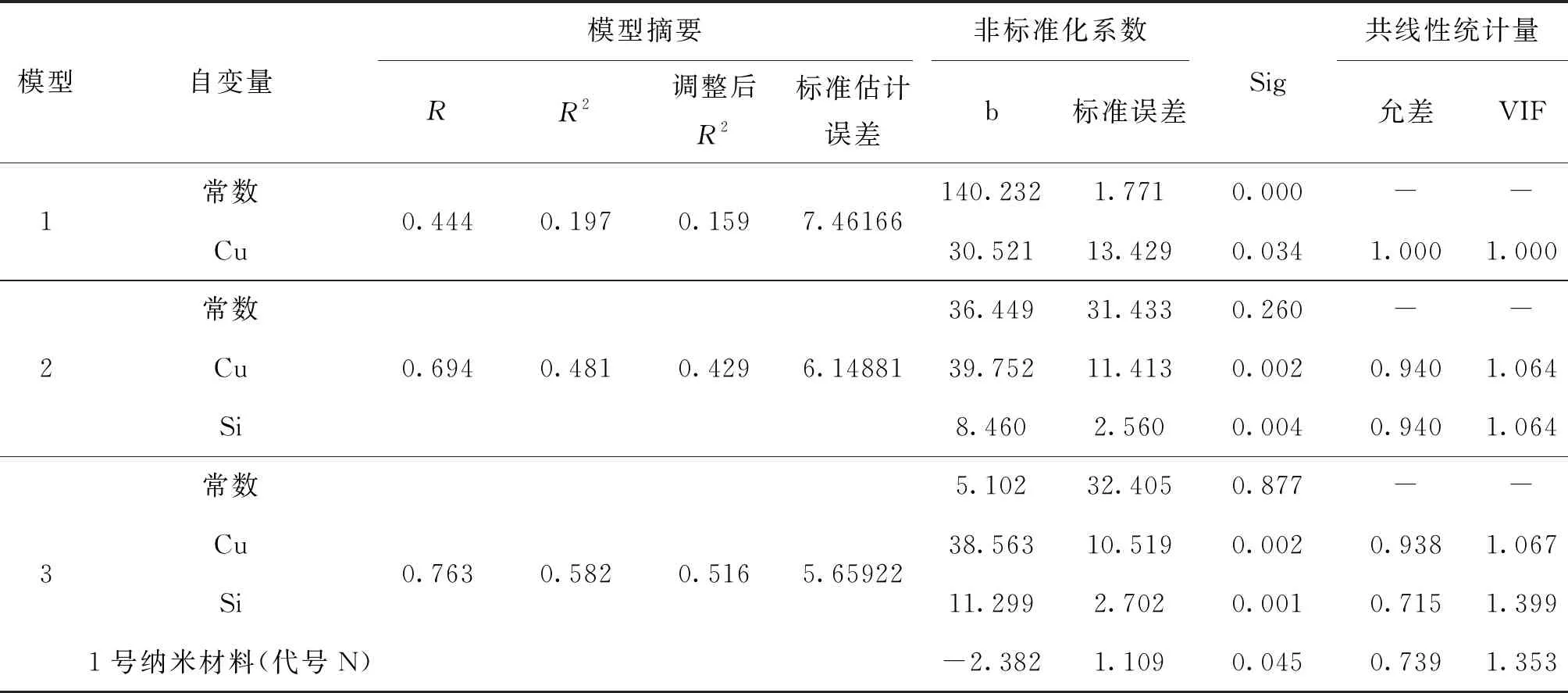
表3 屈服强度建模数据

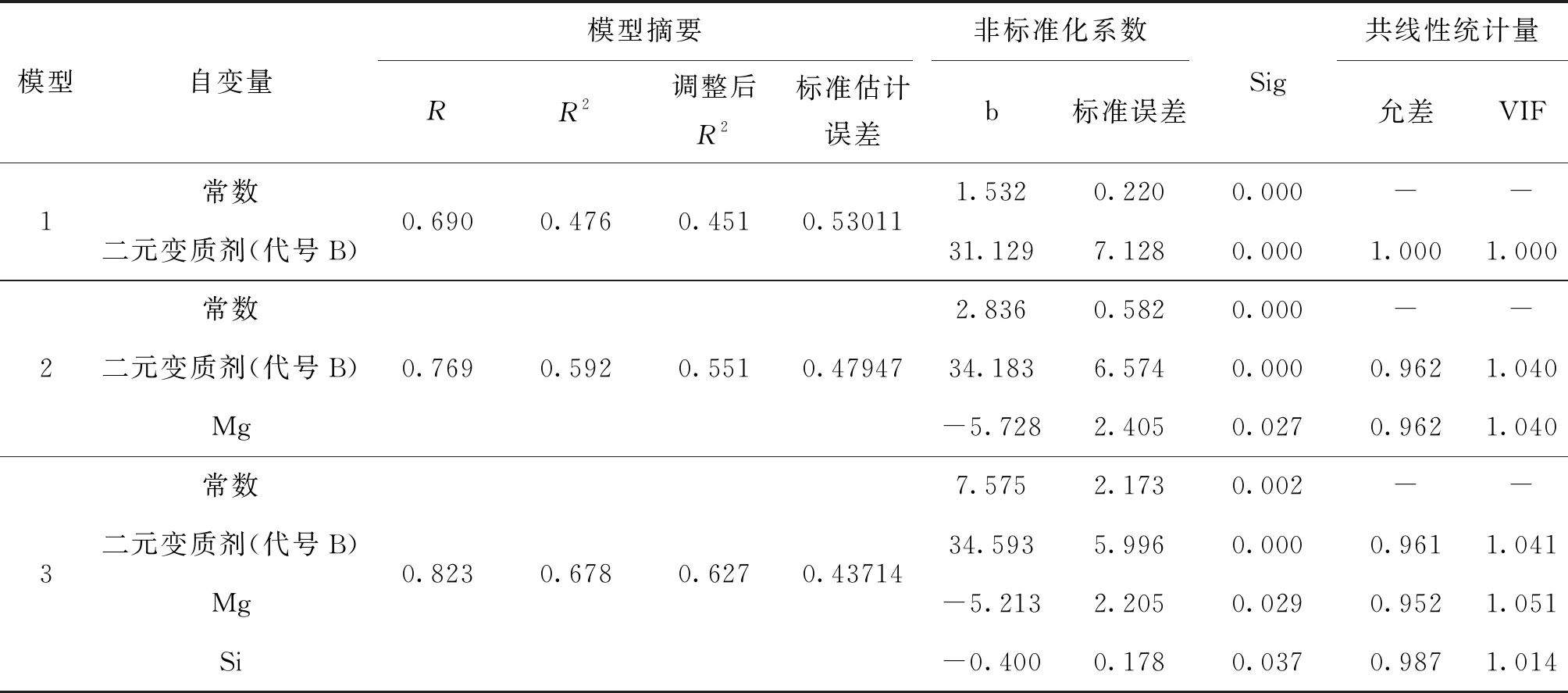
表4 伸长率建模数据

通过数据分析，拟合的模型能有效反映这三个自变量对因变量伸长率的因果关系影响的客观性．伸长率模型的方程为：YS=7.575-0.4Si-5.213Mg+34.593B.

3.4 硬度作为因变量建模

按照设定选项运行SPSS，硬度的建模数据详见表5．

从表5可见，软件运行后给出了三个模型，为提高模型的拟合优度，选择模型3．模型3的调整后R2达到了0.701，标准估计误差为最小，表明模型3的拟合优度较好，达到了大效应．从表5数据可得出，Mg的显著性指标Sig值为0.000，表明它对因变量硬度产生的影响具有极显著性，Cu及1号纳米材料的显著性指标Sig均小于0.05，表明这两个自变量对因变量硬度所产生的影响具有显著性，它们所建立的线性关系回归系数存在且回归模型较好，回归方程具有统计学意义． Mg和Cu及1号纳米材料三个自变量多重共线性检验指标VIF的值都远低于10，表明这三个自变量之间不存在多重共线性，它们之间的作用程度不影响各自效应分析的准确性．

表5 硬度建模数据

通过数据分析，拟合的模型能有效反映出这三个自变量对因变量硬度的因果关系影响的客观性．硬度模型的方程为：YY=59.87+12.642Cu+41.7Mg+0.709N.

3.5 导热系数作为因变量建模

按照设定选项运行SPSS，导热系数的建模数据详见表6．

表6 导热系数建模数据

从表6可见，软件运行后只有一个模型，调整后R2只有0.167，拟合优度一般，达到中效应程度．从表6数据可得出，Mg的显著性指标Sig值小于0.05，表明这个自变量对因变量导热系数所产生的影响具有显著性，它们所建立的线性关系回归系数存在且回归模型较好，回归方程具有统计学意义．Mg的自变量多重共线性检验指标VIF的值为1，远低于10，表明不存在多重共线性，不影响自变量效应分析的准确性．

通过数据分析，拟合的模型能有效反映出自变量对因变量导热系数的因果关系影响的客观性．导热系数模型的方程为：YD=201.393-95.27Mg.

4 模型组合及辅助设计方案[3]

4.1 目标性能指标

开发的铝合金材料需要同时满足特定的性能：压铸抗拉强度YK≥270 MPa、压铸屈服强度YQ≥160 MPa、压铸伸长率YS≥1.8%、压铸硬度YY≥78 HBW及材料导热系数YD≥172 W/mk．这些性能在表1的23组试验数据中没有一组能同时满足要求，因此需要通过模型组合来辅助设计出新的方案．

4.2 模型组合及其运算

将5个性能的模型组成方程组(1)：

(1)

将目标性能指标代入方程组(1)，经变换得方程组(2)：

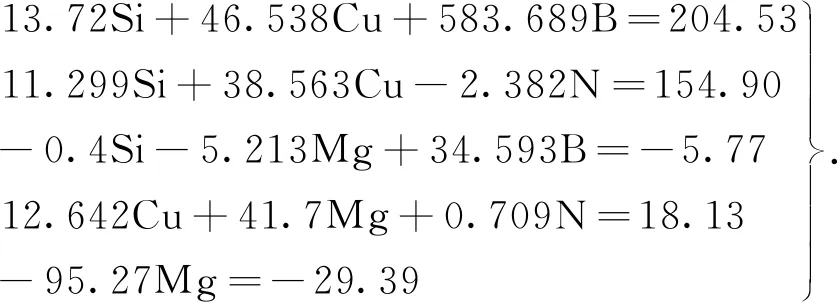
(2)

将方程组(2)等式左边的系数组成矩阵(3)：

(3)

其逆矩阵为：

(4)

将方程组(2)等式右边的数值组成如下的列矩阵：

(5)

运用矩阵解方程组(2)，得：

当w(Si)=12.576%，w(Cu)=0.376%，w(Mg)=0.309%，w(1号纳米材料)=0.716%和w(二元变质剂)=0.025%，就能同时实现五个因变量特定的目标性能，即抗拉强度270 MPa、屈服强度160 MPa、伸长率1.8%、硬度78 HBW、导热系数172 W/mk的自变量数值，也就是设计方案中主要成分和两种变质材料加入量质量比例的理论值．

4.3 模型预测

考虑到实际生产中成分控制的波动性，将方案的控制范围调整到：w(Si)=12.6%～13.1%，w(Cu)=0.4%～0.6%，w(Mg)=0.3%～0.26%，w(1号纳米材料)=1%～2.5%，w(二元变质剂)=0.025%～0.03%．选择这个控制范围，在期望满足性能指标的同时具有工况条件下的可操控性．

将调整方案后的5个自变量控制范围分别输入到5个模型方程中，所得结果列于表7．

从表7可看出，只要3个主要成分Si，Cu，Mg和变质材料的加入量都控制在一定范围内，可通过模拟同时达到5个目标性能的指标．

表7 主要成分和变质材料加入量控制范围内预测的目标性能

4.4 设计方案的验证

所设计的模型是否精准并指导实践，还需通过实践来验证．按照所设计的模型计算出主要成分Si，Cu，Mg和变质材料的加入量，然后进行验证试验，并对试验产品进行性能测试，测试结果列于表8.由表8可知，试验产品的性能均达到目标要求，运用SPSS软件线性回归建立的模型，在开发高强高导热压铸铝合金材料中得到了试验的验证．

表8 试验产品的性能测试

需要注意的是，在运用SPSS软件回归分析建模辅助设计开发铝合金新材料时，不能只依赖模型的数学计算结果，应以符合材料的冶金基本原理为前提．当元素之间交互作用明显、分析中出现多重共线性时，需要进行多重共线性处理，以排除分析误差．当模型组合的运算结果中出现某元素成分为负数时，说明不符合实际，需要调整目标性能指标进行重新拟合运算．

5 结 论

(1)运用SPSS软件设定合适的选项，可快速地进行回归分析并建立数学模型，建立的模型可用于生产预测．

(2)将SPSS应用于开发铝合金材料的过程中，可根据不同的元素成分及工艺条件等对各种性能的影响作用建立相应的模型，有利于在定性分析的基础上进行定量分析．

(3)多个模型的有机组合及其运算，对于特定性能铝合金新材料的开发，在数学模拟上可以起到方案设计的辅助作用．