构建学习任务型课堂 让数学学习真正发生——《除数是小数的除法》教学片断与反思

王淑珍

众所周知，知识的掌握和能力的培养都离不开学习的主体——学生自身的智力活动，这是任何其他因素都无法代替的一种特殊的认识活动。所以教学中必须做好两件事：一是调动学生主动学习的心态，让学生积极参与学习；二是要使学生形成良好的认知结构，最终促进学生知识的内化。因此，我们要努力构建学习任务型课堂，让数学学习真正发生。以下便以《除数是小数的除法》教学片断为例谈学习任务型课堂的构建。

【片断】例：0.065千克是0.05千克的几倍?

一、比较

学生列出算式 0.065÷0.05之后,我引导学生把该算式与准备题中的 14.4÷18、6.21÷3 进行比较：“你发现了什么？”

生1：我发现除数变小数了。

生2：原来是小数除以整数，现在变成小数除以小数了。

二、猜测

师：像这样的除数是小数的除法，同学们猜猜看，应该怎么计算呢？

（一石激起千层浪）

生1：我猜是把被除数和除数都变成整数。

生2：那可不一定，根据商不变性质把被除数和除数同时扩大相同的倍数，这样除数就可以变成整数了。

生3：我也认为只要把除数变成整数就行了。前面我们不是已经学过除数是整数的小数除法了吗？

生4：又是把新知转化成旧知。

三、探索

1．独立尝试。

此时，学生的猜测已接近新知的关键所在。我抓住这个契机，引导学生独立尝试，探索计算方法，再在小组里进行交流。

2．算法展示。

3．交流评价。

算法①的学生：我把0.05看成5，然后让商的小数点和被除数的小数点对齐。

（话音刚落，马上有人反驳）

生1：不对！除数变成5，扩大了100倍，那被除数怎么不变呢？

生2：我通过估算，发现商和除数相乘的积共有五位小数，而被除数却只有三位小数。其实刚才我自己也是这样做的，现在我发现错了。

我马上对这一回答给予表扬：“你很会思考！能通过估算先推翻自己，再判断别人。”这时，同学们都对他投去了赞许的目光。

算法②的学生：我先把除数扩大100倍变成整数，要使商不变，被除数也要扩大100倍，然后按照除数是整数的小数除法的法则来做。

师：大家说有没有道理？

同学们自发地报以掌声。其中一个学生很真诚地说：“我觉得他写得很清楚，讲得也很清楚。”

而这时，算法③的学生很不好意思地站了起来：“老师，我知道自己做错了！”

我内心为该学生能发现并承认自己的错误而欣喜，但表面上故作惊讶：“哦，是吗？你把自己的做法说说看好吗？”在我的鼓励之下，他“暴露”了自己原先的想法，并立即纠正。

“咦！第④种算法你们能理解吗？”我故意把这个“球”抛给学生。在倾听了学生的想法之后，我给予了肯定。但个别学生不“肯”了：“这样做太麻烦了！还要转化单位。”

在算法⑤的学生表达自己的意思之后，我引导学生进行优化：“你们认为哪种是最佳算法？”

生1：我觉得第②种最简便！只要把除数转化成整数就可以了。

（教师随即在第②种上作“☆”记号）

生2：不！我认为第⑤种才是最佳方法。

生3：第⑤种和第④种都太麻烦了！我认为没有必要把被除数和除数都变成整数。

生4：况且第④种算法有局限性。如果没有给你提供单位呢？

……

师生共同归纳“除数是小数的除法”的一般算法。

【反思】

如何构建学习任务型课堂呢？我认为至少要做到把以下三个要素“还给”学生。

1．把时间还给学生，让学生主动参与任务。

“学生是数学学习的主人，教师是数学学习的组织者、引导者与合作者。”从这个理念出发，教师应从“占有”课堂的历史舞台上退出来，把主动学习的时间还给学生，给时间才会有发展，给时间才能为任务型课堂提供基础和保障。案例中，当学生经过观察，发现新旧知识间产生了认知冲突后，我便鼓励学生进行猜测与探索。试想：如果没有足够的时间，怎会出现探索后的算法多样化？如果没有足够的时间，学生怎有机会充分展示自己的思维过程？更谈不上会有反思之后的自评与他评。

纵观本课教学，我给学生提供了近三分之二的时间，让其经历比较、猜测、尝试、交流、评价、归纳的过程，从而避免了学生主动参与的“表面化”，而让数学学习真正发生。

2．把思考还给学生，让学生自主完成任务。

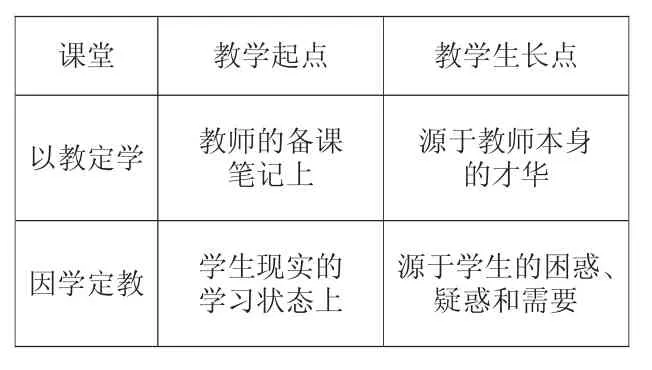
课堂 教学起点 教学生长点以教定学 教师的备课笔记上因学定教 学生现实的学习状态上源于教师本身的才华源于学生的困惑、疑惑和需要

在讲授新知中，处理教材和选择教法不是“给予”，让学生“吃现成饭”，即轻而易举得出结论；而是千方百计调动学生的积极性并创造条件，引导学生悟出道理，发现结论。

因此，在课堂上我们应坚持把思考还给学生，根据学生已有的认知水平，在其最近发展区附近，让学生自主探索，合作交流，让学生真正去经历“做数学”的过程。在本案例中，我引导学生发现新旧知识的“生长点”（除数是整数的小数除法）之后，鼓励他们去猜测探索、合作交流，促使学生进入思考的状态。在这一思考的过程中，学生的思维被激“活”了：（1）出现了算法多样化，这是第一层次的思考。我们的教材只是简单地呈现了一般算法，即案例中的第②种，但学生由于个体思维水平、知识经验和思考角度的不同，出现了五种算法，每一种算法都是他们经过探索、思考得出的富有个性和创新性的结果。（2）在算法多样化的基础上，学生自发地、积极地进入了再思考的阶段，他们充分展示了自己的思维过程。尽管有两种算法是错的，但却看似错得有依据，错得合理（受“除数是整数的小数除法”的负迁移），更何况错误本身就是重要的教学资源，既给学生的再思考提供了有效的载体，同时让原本算法错误的学生在同伴的批评引导下进行反思，重新改进之后也体验到成功。尽管有两种算法并不高效，但我们首先尊重学生的算法，继而进行优化，学生集体评议，观点交锋，形成了课堂思辨的高潮，完善了自身的认知结构。

3．把评价权还给学生，让学生在评价中学会评价。

当前的课堂教学教师不应是学生学习的唯一评价者，既然评价目标是多元的，那么评价主体也应是多样的。课堂教学中，不妨适时地把评价权还给学生（包括他评、自评等），让他们在相互评价中学会欣赏他人，吸纳意见，随时进行自我反思、自我完善。在案例中，学生创造性地占有了课堂，自主地对五种算法进行评价，课堂上演了一场“头脑风暴”，学生在相互的评价中学会了评价，发展了自我。

总之，在教师引领学生探究新知的过程中，只有引导学生主动积极地“获取”知识，从知识的形成过程中去顿悟、去发现，才能完成知识的内化，而越俎代庖的简单给予是不利于学生知识内化的。只是告诉，会忘记；只是演示，会记住；如果参与其中，就会明白。因此，只有构建学习任务型课堂，让学生经历“做数学”的过程，才能让数学学习真正发生。