教育的深度智慧：从“学会”走向“会学”——特级教师张冬梅《和的奇偶性》教学片断赏析

季 云

片断一 提出猜想，引发探究

活动一：快速判断下面的数是奇数还是偶数？

52 243 3562

师：判断的方法是什么？

活动二：判断下面算式的和是奇数还是偶数？

66+8+7+9+11+……+29+31+33

师：你觉得是奇数还是偶数？

（学生猜测奇数、偶数的都有）

师：学数学能这样猜测吗？像这样判断一个算式的和到底是奇数还是偶数，就是这节课学习的内容。（板书课题：和的奇偶性）

【赏析：探究“和的奇偶性”，一个数的奇偶性是基础。快速判断一个数的奇偶性，勾起学生对奇数和偶数特点的回忆，为新知的探索做好铺垫。同时，直接抛出一个加法算式，让学生判断和的奇偶性，引起学生猜想，引发质疑，从而激发学生的探索欲望，为接下来的学习留下悬念。】

片断二 初步探究：两个数和的奇偶性

师：要研究若干个数的和是奇数还是偶数，可以先从几个数来研究？

生：两个数，从简单的研究起。

师：怎样研究呢？

生：多举几个例子。

（学生自主探究，完成“研究一”）

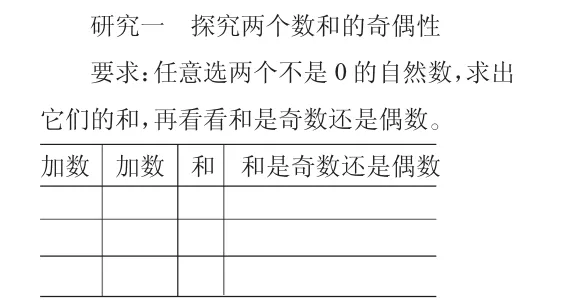
生：1+13=14，和是偶数；4+20=24，和是偶数；5+10=15，和是奇数。说明奇数+奇数的和是偶数，偶数+偶数的和是偶数，奇数+偶数的和是奇数。

生：我发现的规律是一样的，但举的例子不一样。3+9=12，和是偶数；3+8=11，和是奇数；22+12=34，和是偶数。说明奇数+奇数和是偶数，奇数+偶数和是奇数，偶数+偶数和是偶数。

师：你们都说到了奇数+偶数和是奇数，那么偶数+奇数的和是什么数呢？

生：奇数，与奇数+偶数一样，运用了加法交换率，和不变。

教师板书：

奇+奇→偶；奇+偶→奇

偶+偶→偶；偶+奇→奇

师：一个例子得到一个发现，这样发现的规律可靠吗？

生：不可靠，需要多举几个例子来验证。

师：个别例子得到的规律只是一种猜想，还需要去验证。

（学生举例，教师板书：6+7=13、7+6=13、4+6=10、31+67=98……）

师：有没有反例？会不会有漏网之鱼呢？

生：不会，偶数末尾是 0、2、4、6、8，奇数末尾是 1、3、5、7、9，和是奇数。

师：（竖起大拇指）真了不起，这位同学虽然说的还不完整，但他已经在尝试解释“为什么”了。

展示学生画图思考的作品，引导理解并出示课件：

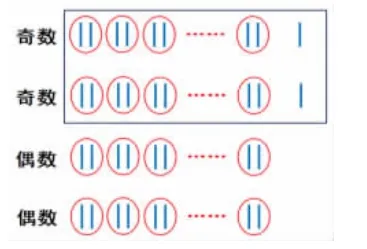
师：什么情况下和为偶数？什么情况下和为奇数呢？

生：奇数+奇数、偶数+偶数，和为偶数；奇数+偶数、偶数+奇数，和为奇数。

教师完善板书：

师：闭上眼睛，打开书本上任意两个相邻页码，和会是什么数呢？

生：奇数，相邻两数一奇一偶，和为奇数。

【赏析：“要研究若干个数的和是奇数还是偶数，可以先从几个数来研究？”让学生任意选两个不是0的自然数，多举几个这样的例子，并求出它们的和。引导学生观察前面得到的若干例子，初步发现其中存在的规律，并在此基础上提出进一步的猜想，同时，要求学生通过进一步的举例，验证自己的猜想。教学并未止步于此，这样的举例始终是个例得到的发现，仍是一种“不完全归纳”。怎样才能培养学生数学探究学习中思维的严谨性和科学性呢？此时，教师一语道破天机，“有没有反例？会不会有漏网之鱼呢？”引导学生将个例性的表象上升到数学的本质，尝试解释“为什么”的问题，有的学生从“数的末尾”的角度去解释结论，更难能可贵的是还有的学生画图解释了其中的数学道理。】

片断三 深入探究：几个数和的奇偶性

师：接下来，该研究几数相加的和了？

师：（板书：32+142+25）这个算式的和是奇数还是偶数？

生：32+142=174，偶+偶=偶，174+25=199，偶+奇=奇，所以偶+偶+奇=奇。

师：用好规律可以去推想多数相加的和的奇偶性。那么接下来你们打算自己研究还是跟着老师去学习？

生：自己研究。

师：现在是举具体的例子还是只要写奇数、偶数相加的形式？

（学生继续探究，完成后汇报交流）

生：从数的奇偶性来看，奇+奇+偶=偶，举例说明1+1+2=4、3+3+4=10，奇数+奇数=偶数，偶数+偶数=偶数。

生：画图来看，奇+偶+奇+偶+奇=奇。（图略）

师：（把多名学生的作品集中起来比较）你发现了什么？

生：无论多少个偶数相加，和都是偶数；和的奇偶性跟奇数的个数有关。

（学生进一步探究，完成“研究二”）

学生汇报，教师课件出示：

师：和的奇偶性和奇数的个数有怎样的关系呢？

生：有奇数个奇数相加的和是奇数，有偶数个奇数相加的和是偶数。

师：算式中有10个奇数，和是什么数？15个奇数呢？

师：（出示课始的连加算式：66+8+7+9+11+……+29+31+33）和是奇数还是偶数？

生：有14个奇数，和是偶数。

师：关键是要知道什么？

生：奇数的个数。

【赏析：学生在第一段的探究活动中，已经获得了一定的活动经验，又考虑到新的探究内容本身的特点，在探究几个数和的奇偶性时，学生任选几个数列出连加算式后，直接要求他们根据前面探究的结论和体会先想想和是奇数还是偶数，再让他们加以验证。接下来，考虑到完全自主地发现其中的规律可能存在一定难度，教学又通过集中学生不同的作品引导他们进一步分析决定几个数连加的和是奇数还是偶数的原因，启发学生透过现象把握本质，从而透彻地理解隐藏于现象中的数学规律。学生通过自主探索与合作交流，了解两个或几个数的和的奇偶性，初步让学生切实经历举例、观察、猜想、验证、归纳、总结等数学活动的完整过程，探究其中所蕴含的数学规律，感受由具体到抽象、由特殊到一般的探索发现方法，进一步发展学生的数学思考。】

片断四 总结反思，提炼经验

师：不知不觉复杂的问题解决了，我们是怎么解决这些复杂的问题的？又是如何寻找规律的？

生：从简单的问题入手，先研究两个数和的奇偶性。

生：然后研究几个数相加的和的奇偶性。

生：从两个数和的奇偶性我们发现了一定的规律，然后举了很多例子进行验证。

师：是的。我们研究复杂的问题，就是应该从简单的问题入手，最后再解决复杂的问题，而我们“发现规律”则需要通过举例，有了初步的猜想，然后再进行验证，从而发现规律，解决复杂的问题。

【赏析：组织回顾和反思活动，侧重引导学生对规律的探索和发现过程进行反思，以提炼出探索数学规律的基本步骤和方法。解决复杂问题，可以从简单问题入手研究，探索并寻找规律解决复杂问题。探索规律时，可以举出一类例子，通过观察比较，从不同的算式中寻找共同的特点，就可以从中发现规律。举例、比较并进行验证，都是探索规律常用的方法。让学生在整个活动过程中不断获得积极的情感体验，从而增强对数学学习的兴趣，促进乐于思考、勇于质疑、大胆猜想、细心验证等良好学习品质的形成。整个教学设计着眼于引导学生从“学会”走向“会学”，发展学生的数学素养。】