一种输入有界的四轮全向机器人轨迹跟踪控制方法
2019-07-25王建彬陈建平
王建彬,陈建平
(肇庆学院计算机科学与软件学院,肇庆526061)
0 引言
全向移动机器人运动灵活,凭借着不改变位姿就可以向任意方向移动的独特运动优势,已经被广泛应用于人类的生产、生活实践中,与之相关的控制问题越来越受到人们的重视,轨迹跟踪就是其中的一个重要研究内容[1-2]。
目前关于全向机器人轨迹跟踪控制方法研究主要集中在基于运动学模型和动力学模型两方面[3]。文献[4]中针对一种四轮正交的全向机器人的轨迹跟踪问题,基于动力学模型采用状况反馈方法设计了机器人的非线性控制器。全向机器人轮系复杂,在运动过程中极易受到各轮间摩擦不一致、被动轮不可控、堵转等各种问题的干扰,为此考虑到四轮全向机器人系统的模型不确定性及干扰问题,文献[5]设计了一种滑模轨迹跟踪控制器,尽管滑模控制方法可以较好的处理模型不确定性及外部干扰,但是却存在抖振问题。文献[6]针对三轮全向移动机器人的模型不确定性,提出一种模糊PI 轨迹跟踪控制器,利用模糊方法识别跟踪位置和角度。相对于具有两个轮子或者三个轮子的非完整移动机器人,四轮全向移动机器人拥有更加复杂的动力学模型,在实际应用中很难获得精确的动力学模型参数,而且模型结构自身也具有很大的不确定性,同时由于外界干扰等因素的影响,均大大增加了动力学控制器的设计难度。为此在满足一定控制精度或功能的前提下,一部分轨迹跟踪问题的研究是基于运动学模型的。文献[7]针对一种全向移动机器人基于牛顿机械学建立了它的动力学模型,并依据该学模型设计了全局稳定的轨迹跟踪控制器。文献[8]基于反步方法设计了三轮全向移动机器人的非线性控制器,同时采用平方和(Sum of squares)技术对控制参数进行优化,提高了控制性能。文献[9]在研究全方位轮式康复训练机器人的轨迹跟踪问题时,将跟踪控制与干扰抑制归结为L2 设计问题,构造了满足干扰抑制的跟踪控制器。尽管运动学模型相对简单,但当跟踪过程中存在初始偏差或者期望轨迹不连续时,传统的控制法会产生速度突变问题,即要求机器人在瞬间具有较大甚至是趋于无穷的加速度或驱动力矩,这在实际系统中是不可能实现的。
因此,针对四轮全向移动机器人轨迹跟踪控制中的速度突变问题,提出一种基于有界函数的轨迹跟踪控制方法。首先建立机器人系统的运动学位姿误差模型,接着设计一个合理的有界函数,最后将该函数引入到轨迹跟踪控制器中以平滑控制信号,从而保证整个控制过程中控制量不超限。
1 问题描述
如图1 所示的四轮全向移动机器人示意图中,机器人的四个全向轮不是正交排布,而是前两轮夹角120°,后两轮为90°。其中XOY 为机器人的世界坐标系,xoy 为机器人的本体坐标系,θ为机器人的运动方向,Wi表示机器人的四个轮子,Vi为各轮转速,逆时针方向为正,l 为车体中心到轮子中心的距离,δi为各轮与X 轴的夹角。
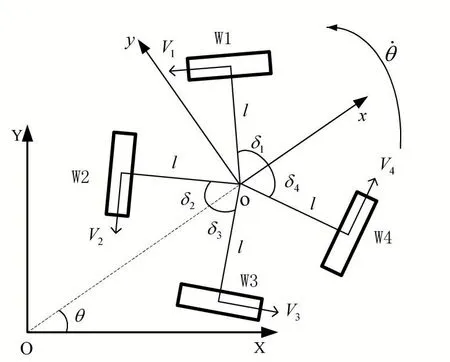
图1 机器人的运动示意图
设任一时刻,机器人质心在世界坐标系和本体坐标中的位姿分别为[X,Y,Ψ]T和[x,y,φ]T,取机器人在本体坐标系速度向量为[u,v,ω]T=[x˙,y˙,φ˙]T,则可得机器人的运动学方程为:

进一步设[Xd,Yd,Ψd]T和[xd,yd,φd]T为两个坐标系中机器人的期望位姿,则有两个坐标系中的机器人位姿误差为:

由图1 以及式(1),考虑到位姿误差有如下关系式成立:
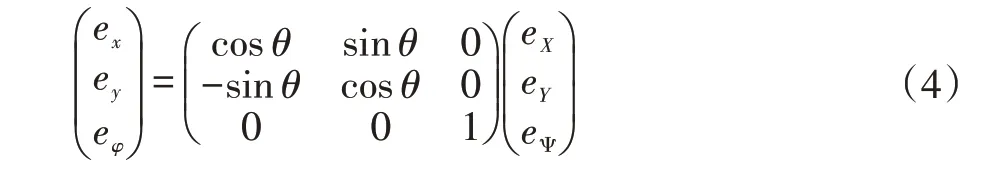
由式(4),当机器人本体跟踪误差趋于零时,世界坐标系中机器人的跟踪误差也趋于零。因此机器人的轨迹跟踪问题转化为:
设计合理的控制律,使系统在该控制律作用下对任意初始误差均可使跟踪误差有界且
2 输入有界的轨迹跟踪控制器设计
2.1 传统轨迹跟踪控制器设计
根据李雅普诺夫稳定性理论,考虑控制系统的李雅普诺夫函数为,则对其两端求导,并结合式(1)、式(4)得:
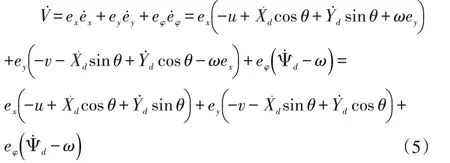
从而得到图1 所示的四轮全向机器人的轨迹跟踪控制律为:

其中k1、k2、k3为正常数。
2.2 有界函数设计
考虑如下函数:
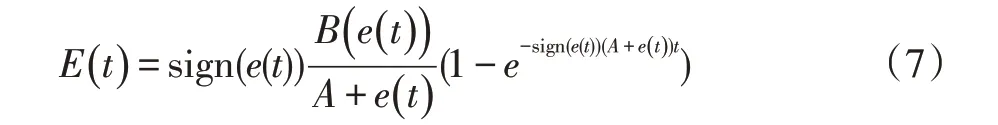
其中A、B 为非负常数,e(t)为本体坐标系下机器人的跟踪误差,sign(*)为符号函数,当e(t)>0 时,sign(*)为正。
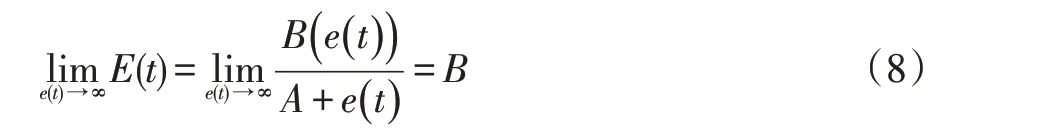
同理可得当e(t)<0,E(t )的取值为-B。
由以上分析可得如下两点结论:
结论1:无论跟踪误差e(t )取值如何,该模型的输出E(t )被限制在[-B,B]范围内;
结论2:在初始时刻t=0,即使e(t )≠0,依然有函数式(7)的取值为E(0)=0,具有平滑的输出。
2.3 输入有界的轨迹跟踪控制器设计
由以上分析可知,式(7)表示的有界函数可以保证输出不超过参数限制,并且具有良好的平滑特性,因此可有效抑制因存在初始误差导致的速度突变问题。用式(7)的输出E(t )代替系统的跟踪误差e(t),并代入式(6)可得四轮全向移动机器人新的轨迹跟踪控制律:

3 控制系统稳定性分析
对于依据控制律(9)所确定的四轮全向移动机器人的轨迹跟踪控制系统,根据李雅普诺夫稳定性理论,取跟踪系统的李雅普诺夫函数为:
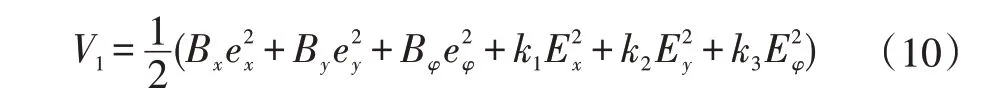
当e(t)>0 时,对式(10)两端求导并由式(7)、(9)整理得:
当e(t)>0 时,由A 以及ki的定义可知,ki>0,Ax+ex>0,Ay+ey>0,Aφ+eφ>0,则有。系统的跟踪误差e(t )而言,总有成立,根据李雅
4 控制系统仿真及分析
为验证本文所设计控制方法的性能,对如图1 所示的四轮驱动全向移动机器人,在MATLAB 2013Ra 平台上进行轨迹跟踪的数值仿真,采样时间为0.01s,机器 人 速 度 约 束 满 足 |u |≤3m/s , |v |≤3m/s ,|ω |≤3 rad/s,从而控制器的参数取为k1=1,k2=1,k3=3,有界函数(7)的参数取为Ax=5,Ay=5,Aφ=6,Bx=3,By=3,Bφ=3。
4.1 直线轨迹的跟踪结果及分析
首先,令机器人跟踪连续的直线轨迹,该直线的轨迹方程为Yd=Xd,期望角度为φd=π/4,假设机器人实际的起始位姿为[1m,-1m,π/2 rad]T,则机器人的初始跟踪误差为[-1m,1m,-π/2 rad]T,具体的跟踪结果如图2所示。
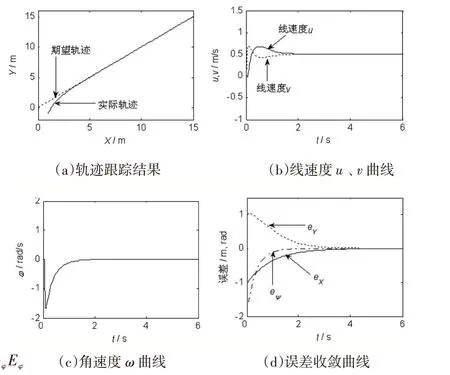
图2 直线轨迹的跟踪结果
由图2 可以看出,对于相对简单的直线路径,即使存在较大的初始误差,机器人也能快速地跟踪期望轨迹,跟踪误差快速收敛到零,在初始时刻,速度控制器的输出也是零,跟踪过程中机器人的线速度和角速度均没有超过各自的约束。
4.2 圆轨迹的跟踪结果及分析
为了验证控制方法对复杂轨迹跟踪的性能,令机器人对一圆形轨迹进行轨迹跟踪仿真,跟踪轨迹的参数方程为Yd=cos φd,Xd=sin φd,φd=t,并且假设在初始时刻t=0 时,机器人的期望位姿为[1m,0m,0 rad]T,实际位姿为[2m,2.5m,π/2 rad]T,则初始跟踪误差为[-1m,-2.5m,-π/2 rad]T,其实际的轨迹跟踪效果如图3所示。
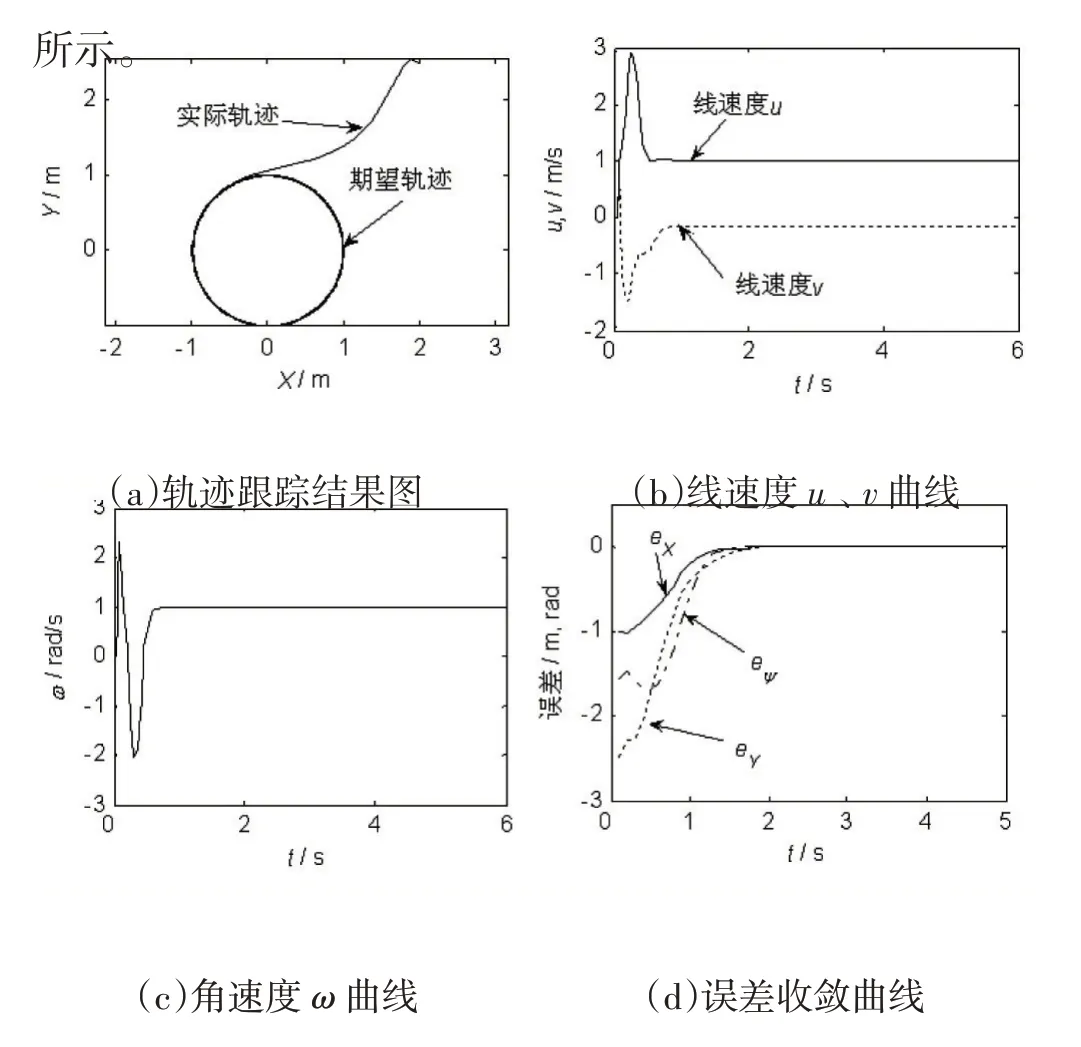
图3 圆形轨迹的跟踪结果
由图3 可知,即使机器人所跟踪的期望轨迹由直线变为时刻在发生着变化的圆形轨迹,本文所设计的全向机器人轨迹控制律仍能保证机器人快速地实现对期望轨迹的跟踪,并且控制器的实际输出线速度u 的最大值为u=2.98m/s,也在其最大速度限制umax=3m/s的范围内,而机器人的另一个输出线速度v 和机器人的角速度ω 也没有超过各自的限制。
综合机器人对以上两种不同轨迹的跟踪结果可以得出,当轨迹跟踪过程中存在较大的跟踪误差时,控制器会产生一个较大的速度输出以使机器人能够快速地跟踪期望轨迹,当误差随时间减小之后,控制器的输出速度逐渐稳定;在初始时刻,即使存在初始误差,控制器也能保证其输出速度为零;对于不同的期望轨迹,该控制方法均能保证机器人能够实现对期望轨迹的跟踪,具体的误差收敛速度与轨迹跟踪的初始误差以及机器人的跟踪速度等因素有关。
5 结语
本文研究了四轮驱动全向移动机器人的轨迹跟踪控制问题,设计了一种可抑制速度突变的轨迹跟踪控制律来进行轨迹跟踪控制。通过设计一个具有平滑输出的有界函数来平滑控制信号,同时结合参数的具体取值以保证控制量不超限。最后使用MATLAB 平台对不同的轨迹跟踪任务进行了仿真实验,一方面通过仿真跟踪结果对比分析,验证了该方法的有效性,另一方面有助于读者更好地理解该方法的基本思想和实现过程。
