基于压缩感知和空间插值的树木内部缺陷应力波层析成像算法

2019-07-25李佳捷杜晓晨

现代计算机 2019年17期

李佳捷，杜晓晨

（浙江农林大学信息工程学院，杭州311300）

0 引言

树木内部缺陷成像技术具有重要的研究价值，使用该技术，能精准、无损地对树木内部健康情况进行检测，从而有效保护各种树木、林木、原木、木材和木质建筑[1]。在众多检测信号中，应力波信号对人体无害且成本低廉，特别适合用于树木内部缺陷检测与成像，已成为本研究领域的主流信号[2]。该成像技术的基本原理是：应力波经过木材缺陷区域的波速比健康区域慢[3]。根据该原理，将若干传感器均匀布置于某树木断层，当敲击其中一个传感器产生应力波时，其余传感器接收该信号并计算出传播时间。由于通过不同材质时波的衰减程度不同，导致所接收的传播速度存在差异，根据所接收传播速度矩阵进行分析、计算和图像重构，最终以二维图像方式直观地显示树木断层内的缺陷情况。

显然，传感器的数量多少是影响应力波成像精度的重要因素[4]。在传统的树木内部缺陷应力波层析成像方法中，均采用固定数量（一般为12 个）传感器组去获得足够进行图像重建的信号。但是传感器的布置过程相对耗时，因此，应减少传感器数量用于信号采集，进行快速层析成像以提高该技术的适用性，同时保证较高的成像精度。本文提出一种基于压缩感知与空间插值的应力波联合层析成像算法，将压缩感知理论与应力波成像相结合，发挥压缩感知对应力波信号稀疏表示和求解的优势，结合空间插值算法恢复非缺陷空间区域的优势，实现树木内部缺陷的快速应力波层析成像。

1 压缩感知原理

压缩感知理论是建立在信号稀疏表示和逼近理论基础上的方法[5]，近年来在医学成像、地震成像、雷达成像等众多领域得到了广泛应用。该原理可以表示为：

其中，x 代表原始信号，需满足稀疏性（或在某个变换域内是稀疏的）；y 代表压缩后的信号；Φ 代表测量矩阵。压缩感知方法就是通过少量的观测次数，在已知测量值y 的情况下，利用凸优化方法求解欠定方程组，高概率地恢复原始信号x。一般情况下，自然信号x 本身并不稀疏，所以需要在某种稀疏基上进行稀疏表示：

其中，Ψ 为稀疏基矩阵，a 是稀疏系数，只有K 个非0 值。通过公式（1）和（2），能得到：

其中，Φ'称为传感矩阵，求解a 的逼近值a'，则能得到原始信号的逼近值x'。基于压缩感知的信号采集过程就是一个线性投影过程，一个向量y（M×1）可以恢复具有K 个非0 值的a。这样，通过少量次数的观测，即可有效地恢复原始信号。

由以上压缩感知原理可知，该方法的关键步骤为：原始信号的有效稀疏表示、测量矩阵的设计和信号恢复算法。其中，测量矩阵通常可以是一个随机矩阵，而欠定方程组的求解问题可转换为L1 范数约束最优化问题进行求解[6]。再由公式（2）可知，压缩感知原理中设计该步骤的目的就是确保原始信号具备稀疏性，从而保证能对欠定方程组进行有效求解。

2 基于压缩感知和空间插值的应力波层析成像

其中，L 表示应力波射线的长度，T 表示应力波的传播时间，V 表示应力波的传播速度，而S 则是应力波波速值的倒数。显然，公式（4）与压缩感知中的公式（3）相似，当空白网格点的尺寸足够小时，S 与a 一样，具备稀疏性，因此，可以用上式表示一次应力波信号采集过程（敲击某个传感器一次后的信号采集过程）。进一步将上式以矩阵形式表示如下：

可以发现，压缩感知原理与层析成像基本反演方程非常相似，它们之间的差异体现在压缩感知对原始信号有稀疏表示过程，这可以理解为该方法的求解基础是强制要求原始信号具备稀疏性。而在树木内部缺陷应力波层析成像领域，用于图像重建的空白网格图本身就具有稀疏性，因此，基于压缩感知原理，可定义如下波速空间分布求解公式：

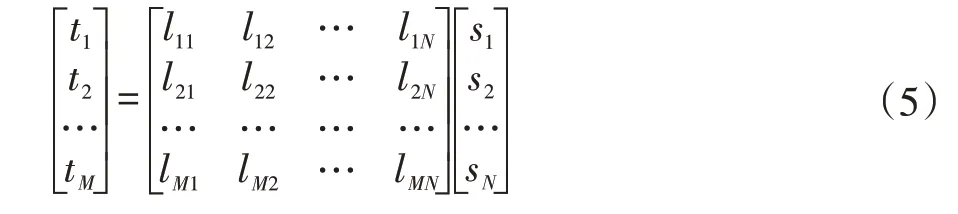
其中，矩阵L 中的每一行对应一条应力波传播射线，lij表示的是第i 条射线，穿过第j 号网格点的距离，N 表示区域中的网格总数，M 表示区域中的射线总数，显然M 远远小于N，这与压缩感知的原理相符，ti表示某条射线对应路径上的应力波传播时间。那么，si就是某网格点中的应力波传播速度分布值（si在网格图中按从左到右，从上到下的顺序排列）。在确定了各个传感器在树木横截面上的布置坐标后，可以得到矩阵L 中的每个值，而向量T 可以通过设备采集（观测）得到，这也与压缩感知的原理相符。

按照压缩感知的原理，可以求解得到公式（4）和（5）中的向量S，依次敲击传感器进行观测后，即可通过少量观测数据和少量观测次数，得到期望的应力波传播速度平面分布。但是，公式（5）与（3）一样，仍然是一个病态方程组，根据压缩感知原理，求解得到的向量S中，仅有少于M 个非0 值。所以基于该方法并不能直接对所有空白网格点进行波速估计，也就不能对树木内部缺陷进行完整的高质量图像重建。

本文的研究目标是在传感器数量减少、采样信号量减少时，仍能对树木内部缺陷进行高分辨率的应力波层析成像。虽然以上提出的基于压缩感知的波速分布求解方法不能直接对缺陷进行高质量成像，但当传感器数量减少时，压缩感知方法能充分发挥其在稀疏采样下的信号表达、求解能力。因此，可以将上述求解得到的波速分布作为应力波层析成像方法中的一个重要参考依据，通过压缩感知方法帮助恢复缺陷区域的潜在空间结构。另外，在项目组的前期研究中，提出过一种基于加权椭圆空间插值的应力波层析成像算法（Ellipse-Based Spatial Interpolation，EBSI[7]），该算法能对树木内部缺陷进行有效的层析成像，但成像结果往往过高估计缺陷的面积大小。通过结论也可以认为：基于EBSI 算法的层析成像结果中，正常木材区域的重建可信度较高，该方法更有助于恢复非缺陷区域的空间结构。基于以上两方面考虑，本文提出了一种基于压缩感知与空间插值的应力波层析成像算法，算法示意图如图1 所示。

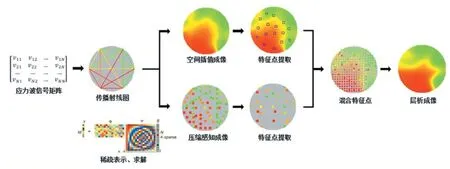
图1 提出的应力波层析成像算法示意图

本算法的基本思想是充分利用压缩感知成像与空间插值成像的各自优势，分别提取两种算法中可信度较高的重建区域内特征点，在统一的重建图像空间中进行混合并最终进行联合层析成像。提出的应力波层析成像算法的具体步骤如下：

步骤1：将所有采集到的应力波传播速度矩阵进行归一化，并完成信号修正[7]。

步骤2：使用EBSI 算法进行应力波层析成像，并进行图像分割，将成像结果分为缺陷区域和非缺陷区域。

步骤3：将修正后的应力波信号按传感器敲击顺序进行分解，每次敲击按公式（5）进行应力波稀疏信号表示和求解。

步骤4：重复步骤3，直到每次敲击都以压缩感知方法进行处理，再将所有求解结果按成像区域网格图进行合并。

步骤5：在压缩感知成像结果中进行特征点提取。

步骤6：在EBSI 成像结果的缺陷区域和非缺陷区域中，分别进行特征点提取。

步骤7：将两类特征点在统一的成像区域内混合，基于经典的IDW 算法进行空间插值。

步骤8：利用统一的颜色尺度可视化网格图，重建树木内部缺陷的断层图像。

3 实验结果

实验环节中，采用了项目组自主研发的应力波信号测量设备进行应力波信号采集[8]。该设备包括12 个应力波传感器、数据线、敲击锤和信号处理箱（如图2所示），信号处理箱将采集到的应力波传播时间矩阵传输到上位机作为算法的输入部分。树木样本则是一个含有真实空洞缺陷的Camphor 树种木桩样本。

图2 应力波层析成像设备

为了生成高分辨率的树木内部缺陷重建图像，每个成像网格点的尺寸设为1 个像素，重建图像的分辨率则为200×200 个像素点。采用红色表示最小波速值（缺陷区域）、黄色表示较小速度值、绿色表示最大速度值（健康区域），以显示理想的传播射线图和木桩断层重建图像视觉效果。此外，为了检验提出方法在信号量不断减少情况下的层析成像性能，分别使用12 个、10 个、8 个和6 个传感器进行了应力波层析成像实验，传感器则按顺时针方向均匀布置于树木横截面。实验环节中，本文还重复了EBSI 方法，并与提出算法进行了对比，以检验压缩感知原理的融入，能否让提出算法在信号量减少的情况下进行高质量缺陷成像。对比成像实验结果如图3 所示。

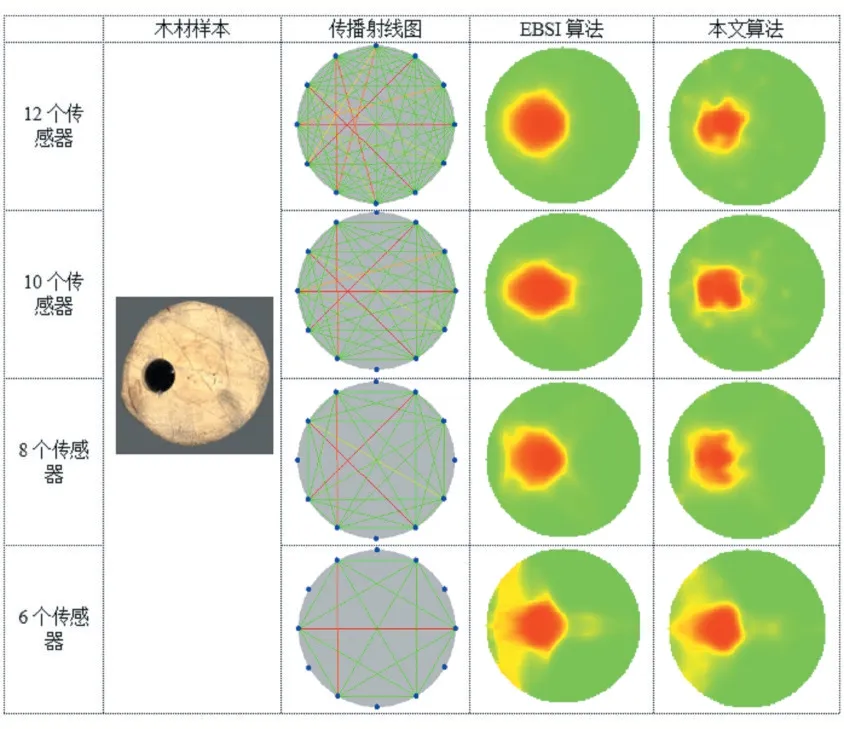
图3 传感器数量递减时的树木内部缺陷应力波层析成像结果

以上对比层析成像实验结果显示，当传感器数量相对充足时，两种算法均能取得较为理想的层析成像结果。但当传感器数量递减时，信号量也逐渐减少（传播射线图即为可视化后的应力波原始波速矩阵），两个算法的成像结果均开始变差，特别是EBSI 算法，当传感器数量减至8 个或6 个时，缺陷区域的成像结果与真实情况差别很大，缺陷图像甚至出现了扭曲、失真等严重错误情况。相比而言，本文提出的算法，当传感器数量减至8 个或6 个时，仍能保证较好的成像效果。该实验结果表明：在信号量不足的情况下，压缩感知方法在稀疏表示、求解方面的优势有助于应力波层析成像算法重建高质量的树木内部缺陷图像。