基于梯度的优化算法研究

常永虎，李虎阳

（遵义医科大学医学信息工程学院，遵义563000）

0 引言

以往建立一个机器学习模型需要清洗数据、找特征、构建模型并训练和应用模型四个阶段。在这个过程当中，时间成本最高的环节是找特征。深度学习由于能够自动找特征，从而降低模型建立的人工时间成本而变得流行，它使工程师只需经历清洗数据、构建模型、训练和应用模型三个阶段就可以完成一个任务。但不管机器学习算法还是深度学习算法，都需经历训练模型阶段。此阶段是计算复杂度最高的阶段，甚至用几百台机器投入几天到几个月来解决模型训练问题也是很常见的。一个好的模型训练算法通常可以降低模型训练的计算复杂度，也可以提高模型的精确度，使模型达到最优结果。在此过程中使用到的算法通常叫做优化算法，梯度下降类算法作为最流行的优化算法之一，目前是神经网络问题中最常用的优化算法。

机器学习类算法研究的热潮不断高涨，各类开源机器学习框架也层出不穷，其中包括Karas、Tensor-Flow、Caffe、MXNet、pandas、scipy 等。虽然这些框架中都已经集成了常用的梯度下降类算法，但不同的梯度下降算法在不同的模型训练中会表现出不同的性能，也不是最先进的梯度下降类算法在所有的模型中都表现最优。因此，本文的目的是通过对比梯度下降类算法在不同模型中的表现，为读者直观地呈现不同梯度下降类算法的效果，从而帮助读者在实际模型训练过程中选择更合适的梯度下降类算法

1 梯度下降类算法

在微积分中，对多元函数的参数求解偏导数，然后以向量的形式将各个参数的偏导数写出来就是梯度。如函数f（x，y），分别对x 和y 求偏导数，求得的偏导数组成的向量是（∂f/∂x，∂f/∂y）就是梯度。梯度下降算法是求解无约束优化问题的最简单、最经典的方法之一。它的目的是找到目标函数J（θ）取极小值点时的θ值，其中参数θ属于Rn空间。它的基本思想是沿着J（θ）的梯度反方向不断的更新θ，并设置一个学习率η决定其每次更新的步长直到J（θ）的结果足够小。以此来达到最小化目标函数的目的。

最原始的梯度下降法叫做批梯度下降法，此方法的基本思路是每次都在整个数据集上计算损失函数关于θ的梯度。然后不断重复计算公式（1），直到梯度接近于0。

此方法是最初的梯度下降算法，通过此方法，可以使计算机通过迭代计算，求解任意具有一阶导数的极值。但也有三类主要问题[1]。第一类问题是计算效率问题，主要表现有两点：①这种方法每更新一次，就需要在整个数据集上计算一次梯度。当数据量非常大的时候，整个算法的就会非常慢且特别吃内存。②每次更新的步长是一个超参数。当更新步长太大时，算法效果出现抖动，通常无法收敛到最佳效果。当更新步长太小时，算法收敛速度较慢且容易陷入局部最小值。第二类问题是梯度计算问题：主要表现在神经网络训练过程中。由于神经网络特征较多导致目标函数有时是一个非凸的函数，此时很难避免参数被困在极小值附近。这类情况常常导致梯度接近于零，所以普通梯度下降法很难从中逃脱。因此，无法收敛到全局最小值。第三类问题是：梯度下降法中的学习率η是一个固定值，常常很难确定η的取值。具体表现为：①如图1 所示：过小的学习率导致目标函数收敛缓慢，而过大的学习率会导致目标函数在其极小值附近剧烈震荡。②由于所有参数都使用相同的学习率，导致数据中出现频率低的特征常常无法达到最优效果。针对梯度下降算法这些问题，图1 总结了相应的三类改进策略及相应算法。

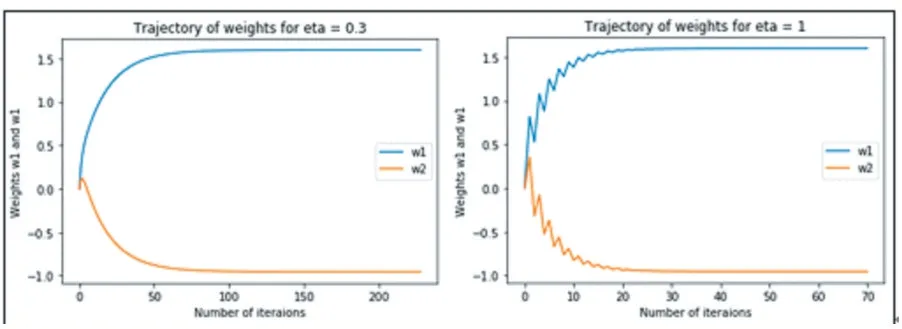
图1 不同学习率收敛震荡对比图

1.1 改进算法计算效率

在样本量极大的时候，对大量相似样本计算其梯度是没必要的。因此，这部分主要通过调整每次迭代计算的样本量提高计算效率。

（1）批梯度下降法

此算法先将所有样本随机排序，然后将样本分组，每次计算只对其中一组数据做优化计算，当所有样本都计算一遍后再重新分组重新计算。若样本被分成N组，则此方法在所有样本都计算完一遍后就进行了N次梯度优化，而原始梯度下降法只能优化一次。因此提高了算法效率[2]。

（2）随机梯度下降法

随机梯度下降法简称SGD（Stochastic Gradient Descent）[3]。SGD 在批梯度下降法的思想上更进一步，它将批梯度下降法的每批数据量降到1，即每次梯度更新只用一个样本。如图2 所示。这种方法加快了收敛速度但同时由于频繁更新参数导致目标函数在剧烈震荡中逐步下降。

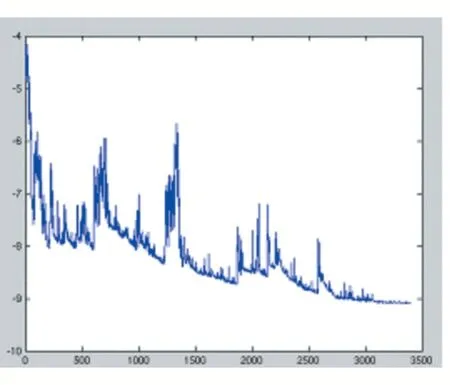
图2 SGC收敛波动（来源：Wikipedia）

综上所述，批梯度下降法和随机梯度下降算法具有相同的优化思路，即都取训练样本的一个子集。因此，算法的好坏主要取决于子集的大小。通常，根据不同的应用场景，小批量的大小取50 到256 较为合适。

1.2 优化梯度计算方法

由于本文主要讨论深度学习中常用的优化的梯度类算法，所以在此不再讨论那些不适用于高维数据的方法，如类似于牛顿法的二阶算法。

（1）动量法

牛顿法[4]将目标函数比作高低不平的地面或山坡，把优化过程比作小球滚下坡的过程。这种方法主要应对那些类似于峡谷形状的函数，可以避免其在峡谷两边震荡而下降缓慢。动量法是在更新向量（梯度向量）之前增加前一次的更新向量，从而在他们相同的方向上累加速度，在不同的方向上减小速度，以此减小震荡，加快收敛速度。

其中：vt表示第t 次的下降动量，vt-1表示t-1 次的下降动量。γ为下降动量的衰减值，通常取0.9。θ 表示要更新的向量。∇θJ(θt)表示第t 次更新时的梯度值，η 表示学习速率。

这种方法能够明显加速SGD 的学习速率并且可以减小SGD 无谓的震荡，但在下降到极值点附近的时候由于速度过快而无法及时停止。

（2）NAG 法

NAG[6]的全称是Nesterov Accelerated Gradient。此方法主要为了解决动量法无法及时停止的问题。NAG认为在t 次更新中会用到动量项γvt-1，所以θ-Vt-1就是参数向量下一个位置。所以，我们与其在当前位置计算梯度还不如在当前位置的下一个位置计算梯度。这样既没有增加计算量，又可以让参数及时的根据梯度修正下降误差。

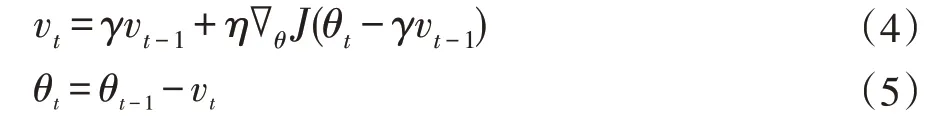
公式中各符号含义与上文相同。从公式可以看出，NAG 法与动量法的区别只在于计算梯度的位置不同。动量项γ的参考值也是在0.9 附近取值效果最好。

图3 SGD、动量法和NAG下降对比

图3 展示了不同梯度下降法在sixhump 函数中的收敛过程。左图为SGD 收敛路径图，中图为动量法收敛路径图，右图为NAG 收敛路径图。图中的每个蓝点代表每次梯度计算后下降的位置。所以，点越稠密表示下降速度越慢；点越稀疏表示下降速度越快。通过对比可看出，SGD 算法每次下降的点与相邻点距离是固定的且非常近，NAG 和动量法都有一段加速区域和震荡区域，但NAG 的震荡明显比动量法弱。

1.3 学习率调整优化算法

学习率对于梯度类优化算法非常重要。尤其在稀疏性很强的数据集中，一个好的学习率调整算法不但能够使目标函数更快地找到极小值，而且可以优化出更精确的目标函数。

（1）AdaGrad 方法

AdaGrad[7]能够根据参数的重要性调整学习率。它能够根据参数更新的平凡程度自动调整学习率。所以它非常适合稀疏性很强的数据集。Dean 等人[8]使用AdaGrad 实现了YouTube 中猫的识别算法。Pennington 等人[9]使用AdaGrad 算法对GloVe 词嵌入网络进行训练并最终使不常出现的词语得到了和经常出现的词语近似的学习率。这种方法在每次更新参数的同时更新学习率。更新方法如公式（6）。

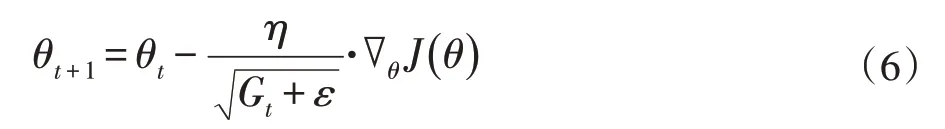
公式（6）主要增加Gt，Gt表示前t 次更名梯度的平方和。通过增加这一项，参数随着更新频率和更新幅度的大小逐渐变小而不影响稀疏属性的更新。除此之外，AdaGrad 的另外一个优点是不需要手动调整学习率，一般直接使用就可以。同时，也注意到公式的分母部分只增不减，使整个学习率随之越来越小直到无限小。

（2）AdaDelta 方法

AdaDelta[10]方法是AdaGrad 方法的改进，主要解决了AdaGrad 方法单调递减学习率的问题。AdaDelta 方法采用指数衰减移动平均的方式来取代AdaGrad 里面将以往全部梯度值都平等纳入平方和的做法。它将上面Gt 的计算方法替换成如下方法：

通过对比可以发现，只要将公式中E[g2]t替换成Gt，AdaDelta 方法就会回退到AdaGrad 方法。这里的γ建议取0.9，而默认的学习率为0.001。

（3）Adam 方法

Adam（Adaptive moment Estimation）[11]是另一种针对调整学习率的方法。这种方法不但像AdaDelta 一样通过收集历史梯度值逐步衰减学习率，还能像动量法一样记录梯度本身的指数衰减值。

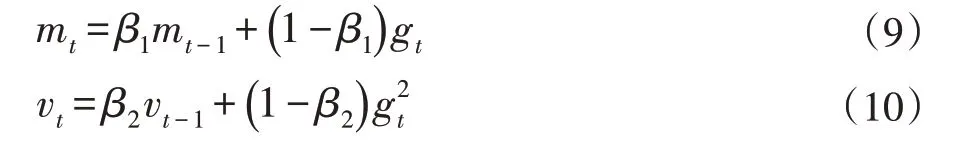
其中，mt和vt分别是梯度的一阶和二阶矩估计。

Adam 的更新规则是：

Adam 作者提出β1、β2和ε 的取值分别是0.9、0.999 和10-8。它的实验结果表明Adam 的实际收敛效果更好且对学习率的调整表现更好。

2 算法比较

前一节提到了三类算法，这些算法在各自不同的角度表现出优秀的效果。在模型训练过程中，影响其训练效果的主要是一些局部极值点。在高维模型中，这种局部极值点更多，各个特征值就可能会有更复杂的分布。一种最难处理的分布是所有维度都处于极值点，但一些处于极大值，另一些处于极小值，这种点被称作鞍点。那么在实际模型训练任务中，各个算法的在鞍点[12]附近的表现如何？

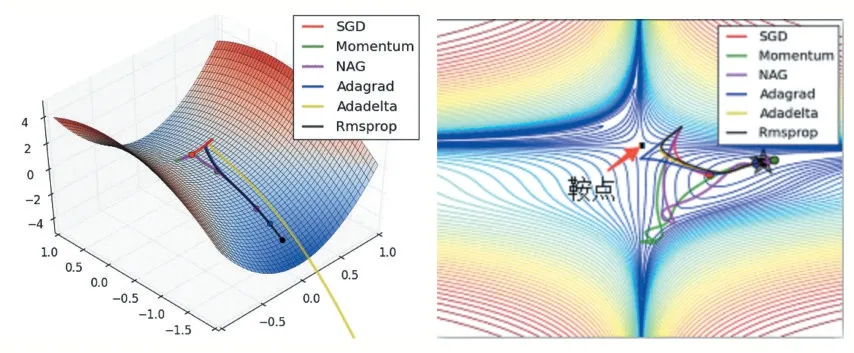
图4 梯度类下降算法在按点附近的表现

从图4 可以发现AdaDelta 首先摆脱鞍点并快速下降，Rmsprop 次之。而SGD 可缓慢摆脱鞍点，动量法处于RmsProp 和SGD 之间。究其原因，主要是AdaDelta方法不会出现扰动，能最先逃出鞍点，SGD 方法在原始梯度下降法基础上增加了随机性，所以可以逃出鞍点，动量法由于保留了之前的优化速率和方向，所以在最初出现震荡区域而导致优化速度比较慢，但逃离鞍点后优化速度越来越快。

如果输入的数据有稀疏性，动态调整学习率的算法会比较好，因为使用者不需要调整学习率，直接使用默认学习率就可以达到较好效果。但也有一些研究成果仅仅使用原始梯度下降算法就可以找到极小值。如果使用者关心算法的收敛速度或者训练的是一个参数较多或隐层较深的网络，就需要选取一个动态调整学习率的算法，因为他们有可能会卡在鞍点附近[13]。

以上是对几种梯度下降优化算法的直观展示与分析。为了验证其在深度学习算法中的表现，本文将在minst 手写数字识别数据集上构建一个三层CNN 网络[14]。网络结构如图5 所示。第一个隐层有512 个神经元，激活函数使用ReLU，Dropout 比例为0.2。第二个隐层有512 个神经元，激活函数为ReLU，Dropout 比例为0.2。输出层有10 个神经元，激活函数使用Soft-Max，输出结果使用onehot 方式表示。

图5 神经网络结构

分别使用SGD，动量法、NAG、AdaGrad、AdaDelta、Adam 六种优化方法训练网络，训练效果如图6 所示。

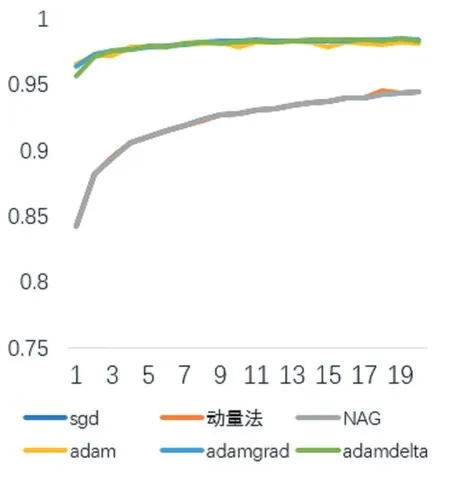
图6 手写数字识别准确率折线图

从图6 中可以看出：SGD、动量法和NAG 的收敛折线基本重合，说明SGD、动量法和NAG 三种方法的收敛速度基本相同；Adam、AdaGrad 和AdaDelta 的收敛折线基本重合，说明Adam、AdaGrad 和AdaDelta 三种方法的收敛速度基本相同。从收敛速度看，Adam 类方法的收敛速度更快；从最终的目标函数准确度看，Adam 类方法的收敛效果更好。

图7 CIRAR-10数据集误判折线图（来源：文献[20]）

实验结果表明，调整学习率的Adam 类算法普遍比动量法类的方法收敛速度快且收敛效果更好。究其原因，主要是因为深度学习类算法省略了特征提取步骤，将所有特征都作为参数进行训练，这是深度学习提高精度的主要原因。但同时，这也使深度学习训练数据变得稀疏。在学习过程中，SGD、动量法和NAG 使用相同的学习率导致稀疏特征无法收敛。Adam 类方法在最初使用较大的学习率，这就使得稀疏特征能够在有限的梯度计算过程中获得更好的收敛效果。也正是由于Adam 类方法最初的大学习率，使得Adam 类方法能够使目标函数在训练之初就能获得较高的准确率。

Adam 类方法与动量类方法相比，即可以摆脱鞍点的束缚又具有较快的收敛速度，那么Adam 类方法是否适用于所有深度学习场景？显然不是。SGD 虽然收敛慢且对稀疏数据的收敛效果没有Adam 好，但SGD方法的泛化能力强，如果使用得当，可以训练出更低错误率的目标函数。文献[20]在CIRAR-10[21]数据集上比较了SGD 和Adam 方法两种方法的训练效果，训练效果如图7。图7 的横坐标表示迭代次数，纵坐标表示目标函数的误判率。从图7 可以看出，虽然Adam 类方法在训练之初的收敛速度较快，且准确率率高于SGD方法，但在第150 次训练后，SGD 的误判率低于Adam方法。这个实验说明，SGD 方法的泛化能力强于Adam方法。

3 结语

本文详细介绍了不同类型的梯度下降算法，并比较了它们在不同数据分布的情况下的收敛速度，同时也比较了它们在稀疏数据中的收敛速度和最终效果。通过比较，我们发现：①对于稀疏数据，自适应学习率的算法表现基本相同且优于其他算法，因此，尽量使用学习率可自适应的优化算法。②如果在意更快的收敛速度，并且训练的算法比较复杂的时候，自适应学习率算法要优于其他算法。③AdaDelta、RMSprop 和Adam是比较接近的算法，在收敛速度和收敛结果方面表现基本无差别。④原始无法跳出鞍点，SGD 方法由于增加了随机性而能够逃出鞍点但收敛速度很慢。⑤SGD方法具有更好的泛化能力，通过优化SGD 方法，并在训练过程中手动调整不同的学习率，在一些非稀疏的数据集上能够得到更好的收敛效果。

除本文着重介绍的SDG 优化策略及其一些变体外，还可以从被训练的数据以及选择模型特点的角度考虑，进一步提高SGD 的性能和目标函数的准确度。例如，一些研究者[22-23]为了使学习过程更加无偏，可以在在每次迭代过程中打乱数据或对数据做有意义的排序；还有一些研究者[24]为了保证学习率在每次迭代过程之前先对数据做0 均值1 方差的标准化等操作；又或者根据梯度类算法的特点，采用相结合的策略或混合策略，对训练集按照训练难度进行递增排序，在不同的时期使用不同的优化算法。